Poissonova konstanta
Úloha číslo: 2152
Odvoďte vztah mezi modulem pružnosti v tahu, smykovým modulem pružnosti a Poissonovou konstantou.
Zápis
E modul pružnosti v tahu G smykový modul pružnosti m Poissonova konstanta Rozbor
Poissonova konstanta je převrácenou hodnotou Poissonova čísla. To vyjadřuje (u kruhové tyče) poměr mezi zmenšením průměru a zvětšením délky při namáhání tahem v oblasti pružných deformací. Hodnoty se pohybují mezi 0 (absolutně stlačitelný materiál) a 0,5 (absolutně nestlačitelný materiál).
Budeme uvažovat tyč. Protože nás zajímá i smykový modul pružnosti, potřebujeme si vyjádřit i tečné napětí a odpovídající úhlovou deformaci. Nejlepší volbou je uvažovat řez tyčí, který je odchýlen o 45° od osy tyče. Tečné napětí na ploše tohoto řezu lze vyjádřit pomocí tahového napětí. Je potřeba určit, o jaký úhel v porovnání s úhlem v rovnici smyku se odchýlí plocha řezu po deformaci. Dále musíme uvažovat prodloužení a zúžení tyče. Tu lze vyjádřit modulem pružnosti v tahu a Poissonovou konstantou a pomocí geometrie je dát do vztahu s úhlovou deformací. Je potřeba brát v úvahu, že uvažujeme malé deformace. Poté už jenom použijeme rovnici pro smyk.
Nápověda
Uvažujte tyč namáhanou tahovou silou. Dále uvažujte řez tyčí, který svírá s osou tyče 45°. Tahovou sílu rozložte tak, aby jedna její složka byla tečná k ploše řezu a druhá k ní kolmá. Vyjádřete tečné napětí na ploše vzhledem k normálovému napětí. Poté si vzpomeňte, co znamená úhel smyku v rovnici pro smyk. Určete, o jaký úhel v porovnání s úhlem smyku se po deformaci plocha řezu pootočí. Nebo uvažujte tento úhel rovnou jako polovinu úhlu smyku a pomocí vhodné geometrie a předpokladu malých deformací to dokažte. Zakreslete si vhodně geometricky obrázek, který bude znázorňovat prodloužení, zúžení a úhlovovou deformaci plochy řezu. Pomocí geometrie, konkrétněji funkce tangens, vyjádřete vztah mezi těmito deformacemi. Ovšem zanedbejte kvadratické členy deformací. Ve vztahu dosaďte z rovnic, které vyjadřují vztah mezi deformací a napětím.
Řešení
Uvažujme tyč namáhanou v tahu silou F a řez, který s osou tyče svírá 45°. Potom sílu působící na plochu tohoto řezu S můžeme rozložit na dvě stejně veliké složky, kde jedna Ft leží v dané ploše a druhá Fn je kolmá k ploše. Jejich velikosti jsou:
\[F_\mathrm{t}\,=\,F_\mathrm{n}\,=\,\frac{F}{\sqrt{2}}.\tag{1}\]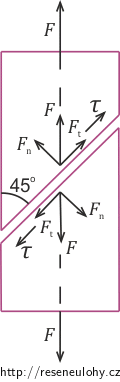
Protože nás zajímá i smykový modul, potřebujeme vyjádřit i tečné napětí τ:
\[\tau\,=\,\frac{F_\mathrm{t}}{S}.\tag{2}\]Když označíme plochu kolmého řezu tyče S0, potom platí:
\[S\,=\,S_0\sqrt{2}.\tag{3}\]Normálové napětí σ, které působí podél tyče, je:
\[\sigma\,=\,\frac{F}{S_0}.\tag{4}\]Dosazením do (2) z (1), (3) a (4) získáme vztah:
\[\tau\,=\,\frac{F}{2 S_0}\,=\,\frac{\sigma}{2}.\tag{5}\]Nemůžeme zde ignorovat sílu Fn, která způsobuje tečné napětí na ploše kolmé k ploše S a též s osou tyče svírá úhel 45°. V podélném řezu tyče si představme čtverec, jehož jedna diagonála leží ve směru osy tyče a na jehož každou stranu působí stejně veliké tečné napětí (ovšem každé orientové tak, aby čtverec byl v rovnováze). To znamená, že když jedna strana je ve směru síly Ft, tedy působí na ni tečné napětí τ, pak symetricky podle osy tyče na sousední straně působí tečné napětí síly Fn. Tečná napětí na ostatních stranách musí splňovat podmínky rovnováhy. Jelikož se osa tyče, tedy i jedna diagonála čtverce, v tahu o žádný úhel nezmění, úhlová deformace se bude týkat pouze stran čtverce. Úhlem smyku γ rozumíme úhel, o který se změní pravý úhel při působení tečného napětí. Ze symetrie lze vidět, že každá strana se deformuje o poloviční úhel smyku. To znamená také to, že plocha S se pootočí o tento úhel.
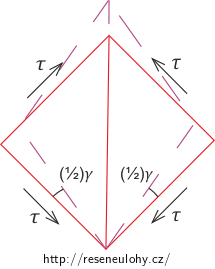
Pokud bychom uvažovali (namísto diagonály) připevněnou jednu stranu čtverce, pak by se jeho diagonála deformovala o poloviční úhel smyku. Lepší představu udělá následující obrázek.
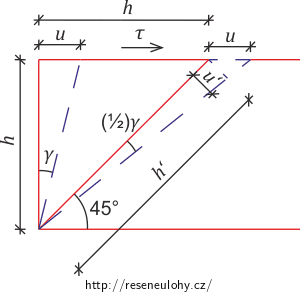
K obrázku je ještě třeba doplnit vztahy plynoucí z Pythagorovy věty:
\[h‘\,=\,\sqrt{2} h, u‘\,=\,\frac{u}{\sqrt{2}}.\]Podle veličin v obrázku můžeme sestavit rovnici:
\[\tan{\frac{1}{2} \gamma}\,=\,\frac{u‘}{h‘}\,=\,\frac{u}{2 h}\,=\,\frac{1}{2} \tan{\gamma}.\tag{6}\]Protože zde uvažujeme dosti malé deformace, vidíme, že rovnost (6) platí, tedy že plocha S se skutečně posune o polovinu úhlu smyku.
Dále si musíme uvědomit, že zatímco se tyč prodlouží, tak se zároveň i zúží. Situaci ukazuje obrázek níže.
Zavedeme si relativní prodloužení:
\[\varepsilon_\mathrm{r}\,=\,\frac{\Delta l}{l_0}\Rightarrow \Delta l \,=\,\varepsilon_\mathrm{r} l_0.\tag{7}\]Pro relativní prodloužení můžeme ještě uvažovat vztah:
\[\varepsilon_\mathrm{r}\,=\,\frac{\sigma}{E}.\tag{8}\]Zrovna tak můžeme uvažovat relativní zúžení:
\[\eta\,=\,\frac{\Delta b}{b_0}\Rightarrow \Delta b \,=\,\eta b_0.\tag{9}\]Protože Poissonovo číslo μ udává vztah mezi prodloužením a zúžením, lze ještě psát:
\[\eta\,=\,\frac{\mu \sigma}{E}.\tag{10}\]Na následujícím obrázku můžeme vidět geometrii deformace plochy S.
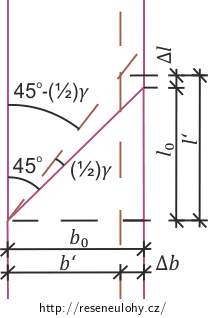
V souladu s obrázkem můžeme dále psát:
\[l‘\,=\,l_0+\Delta l\,=\,l_0+l_0\varepsilon_\mathrm{r}\,=\,l_0\left(1+\varepsilon_r\right)\tag{11}\]a
\[b‘\,=\,b_0-\Delta b\,=\,b_0-b_0\eta\,=\,b_0\left(1-\eta\right).\tag{12}\]Pro další postup je třeba si ujasnit, že vzhledem k tomu, že uvažujeme dost malé deformace, můžeme zanedbávat kvadratické členy. To znamená, že dále zanedbáme členy:
\[\gamma^2, \varepsilon_\mathrm{r}^2, \eta^2, \eta \varepsilon_\mathrm{r}.\]Budeme uvažovat rovnosti:
\[1\approx 1-\frac{1}{4} \gamma^2\,=\,\left(1-\frac{1}{2} \gamma\right)\left(1+\frac{1}{2} \gamma\right),\tag{13}\] \[1\approx 1-\varepsilon_\mathrm{r}^2\,=\,\left(1-\varepsilon_\mathrm{r}\right)\left(1+\varepsilon_\mathrm{r}\right).\tag{14}\]Když se vrátíme k obrázku, můžeme psát:
\[\tan\left(45^\circ-\frac{1}{2} \gamma \right)\,=\,\frac{b‘}{l‘}\,=\,\frac{b_0\left(1-\eta\right)}{l_0\left(1+\varepsilon_r\right)}\,=\,\frac{1-\eta}{1+\varepsilon_r}\approx\left(1-\eta\right)\left(1-\varepsilon_r\right)\approx 1-\varepsilon_r-\eta.\tag{15}\]V (15) jsme využili rovnice }14] a také toho, že b0 je rovno l0.
Použijeme goniometrický vzorec pro funkci tangens:
\[\tan\left(\alpha-\beta \right)\,=\,\frac{\tan{\alpha}-\tan{\beta}}{1+\tan{\alpha} \tan{\beta}}\]a také to, že pro malé α je:
\[\tan\frac{\alpha}{2}\approx\frac{\alpha}{2}.\]Pak:
\[\tan\left(45^\circ-\frac{1}{2} \gamma \right)\,=\,\frac{\tan{45^\circ}-\tan{\frac{1}{2}} \gamma}{1+\tan{45^\circ} \tan{\frac{1}{2} \gamma}}\,=\,\frac{1-\tan{\frac{1}{2}} \gamma}{1+\tan{\frac{1}{2} \gamma}}\approx\frac{1-\frac{1}{2} \gamma}{1+\frac{1}{2} \gamma}\approx\left(1-\frac{1}{2} \gamma\right)^2\approx 1-\gamma.\tag{16}\]Porovnáním (15) a (16) získáme:
\[1-\varepsilon_\mathrm{r}-\eta\,=\,1-\gamma,\]tedy:
\[\varepsilon_\mathrm{r}+\eta\,=\,\gamma.\tag{17}\]Dosazením z (8) a (10) do (17) dostaneme:
\[\gamma\,=\,\frac{\sigma}{E}+\frac{\mu\sigma}{E}\,=\,\frac{1+\mu}{E}\sigma.\tag{18}\]Nyní už zbývá přidat vztah:
\[\gamma\,=\,\frac{\tau}{G}.\tag{19}\]Do (19) dosadíme z (5) a (18):
\[\frac{1+\mu}{E}\sigma\,=\,\frac{\sigma}{2G}.\tag{20}\]Ze (20) můžeme vyjádřit vztah:
\[G\,=\,\frac{E}{2\left(1+\mu\right)}.\tag{21}\]Ovšem podle zadání místo Poissonova čísla μ chceme Poissonovu konstantu m. Vztah mezi nimi je:
\[\mu\,=\,\frac{1}{m}.\tag{22}\]Dosazením (22) do (21) již dostáváme hledaný vztah:
\[G\,=\,\frac{E m}{2\left(m+1\right)}.\]Poznámka: Protože pro Poissonovu konstantu platí:
\[0<\mu<\frac{1}{2},\]pak musí platit i:
\[\frac{E}{3} < G < \frac{E}{2}.\]Poznámka
Tato úloha se dá ještě stručněji vyřešit pomocí zobecněného Hookova zákona (pro izotropní materiály):
\[\sigma_{ij}\,=\lambda\delta_{ij}\left(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}\right)+2\mu\varepsilon_{ij},\tag{1}\]kde λ a μ (pozor, neplést si s Poissonovým číslem) jsou takzvané Laméovy koeficienty. Budeme nyní uvažovat tah, takže jestli tah uvažujeme ve směru x, tak musí být:
\[\sigma_{xx}\ne 0, ij\ne xx\Rightarrow\sigma_{ij}\,=\,0.\tag{2}\]Poznámka: Jestliže i je různé od j, pak z (1) a (2) plyne:
\[0\,=\,2\mu\varepsilon_{ij}\tag{3}\]a to znamená, že platí:
\[\varepsilon_{xy}\,=\,0, \varepsilon_{xz}\,=\,0, \varepsilon_{yz}\,=\,0.\tag{4}\]To je v souladu s tím, že se jedná čistě o tah, takže se neprojevují úhlové deformace. S ohledem na symetrii je tedy nulových šest složek deformace z devíti.
Pro i rovno j získáme z (1) a (2) tři rovnice:
\[\sigma_{xx}\,=\lambda\left(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}\right)+2\mu\varepsilon_{xx},\tag{5}\] \[0\,=\,\lambda\left(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}\right)+2\mu\varepsilon_{yy},\tag{6}\] \[0\,=\,\lambda\left(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}\right)+2\mu\varepsilon_{zz}.\tag{7}\]Porovnáním rovnic (6) a (7) lze hned vidět:
\[\varepsilon_{yy}\,=\,\varepsilon_{zz}.\tag{8}\]Když dosadíme z (8) do (6), dostaneme:
\[0\,=\,\lambda\left(\varepsilon_{xx}+2\varepsilon_{yy}\right)+2\mu\varepsilon_{yy}\,=\,\lambda\varepsilon_{xx}+\left(2\lambda+2\mu\right)\varepsilon_{yy}.\tag{9}\]Vztah (9) dále upravíme na:
\[\frac{\varepsilon_{xx}}{\varepsilon_{yy}}\,=\,-2\left(\frac{\lambda+\mu}{\lambda}\right).\tag{10}\]Poissonovu konstantu m už v podstatě máme určenou v (10), ale je třeba tuto rovnici uvažovat v absolutní hodnotě. To znamená:
\[m\,=\,\left|\frac{\varepsilon_{xx}}{\varepsilon_{yy}}\right|\,=\,\left|-2\left(\frac{\lambda+\mu}{\lambda}\right)\right|\,=\,2\left(\frac{\lambda+\mu}{\lambda}\right).\tag{11}\]Protože uvažujeme, že při prodloužení se tyč zúží, musí být výraz
\[\frac{\lambda+\mu}{\lambda}\]v souladu s (10) kladný.
Teď už zbývá vyjádřit Laméovy koeficienty pomocí modulů E a G. Nyní budeme pro smyk uvažovat (1) obecně, tedy ne přímo pro speciální případ tahu. Pro smykový modul pružnosti platí:
\[2G\varepsilon_{xy}\,=\,\sigma_{xy}.\tag{12}\]Pak podle (1) máme:
\[2G\varepsilon_{xy}\,=\,2\mu\varepsilon_{xy}.\tag{13}\]Takže:
\[G\,=\,\mu.\tag{14}\]Pro modul pružnosti v tahu platí:
\[E\varepsilon_{xx}\,=\,\sigma_{xx}.\tag{15}\]S uvážením (1) a (8) dostáváme:
\[E\varepsilon_{xx}\,=\lambda\left(\varepsilon_{xx}+2\varepsilon_{yy}\right)+2G\varepsilon_{xx}.\tag{16}\](16) dále upravíme na:
\[E\varepsilon_{xx}\,=\lambda\left(1+2\frac{\varepsilon_{yy}}{\varepsilon_{xx}}\right)\varepsilon_{xx}+2G\varepsilon_{xx}.\tag{17}\]Po vykrácení v (17) a pomocí (11) dále máme:
\[E\,=\lambda\left(1-\frac{2}{m}\right)+2G.\tag{18}\]Nyní už z (18) dostaneme:
\[\lambda\,=\,\frac{\left(E-2G\right)}{\left(1-\frac{2}{m}\right)}\,=\,\left(E-2G\right)\left(\frac{m}{m-2}\right).\tag{19}\]Nyní už můžeme dosadit z (19) a (14) do (11), takže:
\[m\,=\,2\frac{\left(E-2G\right)+G\left(\frac{m-2}{m}\right)}{\left(E-2G\right)}.\tag{20}\]Dále:
\[\left(E-2G\right)m\,=\,2\left(E-2G\right)+2G\left(\frac{m-2}{m}\right).\tag{21}\]To ještě lze upravit na:
\[\left(E-2G\right)\left(m-2\right)\,=\,2G\left(\frac{m-2}{m}\right).\tag{22}\]Ještě:
\[E-2G\,=\,2G\left(\frac{1}{m}\right).\tag{23}\]Po další úpravě již máme:
\[E\,=\,2G\left(1+\frac{1}{m}\right)\,=\,2G\left(\frac{m+1}{m}\right).\tag{24}\]Nakonec tedy:
\[G\,=\,\frac{E m}{2\left(m+1\right)}.\]Odpověď
Vztah mezi modulem pružnosti v tahu E, smykovým modulem pružnosti G a Poissonovou konstantou m je:
\[G\,=\,\frac{E m}{2\left(m+1\right)}.\]



