Zrychlený pohyb I
Úloha číslo: 188
Velikost zrychlení hmotného bodu při jeho přímočarém pohybu rovnoměrně klesne během doby 20 s z počáteční hodnoty 10 m·s−2 na nulovou hodnotu. Hmotný bod byl na počátku pohybu v klidu.
a) Jakou rychlost má hmotný bod v čase 20 s?
b) Jakou dráhu za tuto dobu hmotný bod urazil?
Zápis
T = 20 s doba, po kterou klesá zrychlení hmotného bodu a0 = 10 m·s−2 počáteční zrychlení hmotného bodu v(0) = 0 m·s−1 rychlost v čase t = 0 s v(T) = ? (m·s−1) rychlost v čase T s(T) = ? (m) dráha, kterou hmotný bod urazí za dobu T Nápověda 1: Závislost zrychlení na čase
Načrtněte graf závislosti velikosti zrychlení hmotného bodu na čase a napište rovnici příslušné křivky.
Nápověda 2: Závislost rychlosti na čase
Jak získáme závislost velikosti rychlosti na čase, pokud známe závislost velikosti zrychlení na čase?
Jak poté získáme konkrétní rychlost v čase T = 20 s?
Nápověda 3: Závislost dráhy na čase
Jak získáme závislost dráhy na čase, pokud známe závislost velikosti rychlosti na čase?
Jak poté získáme konkrétní dráhu uraženou za čas T = 20 s?
Celkové řešení
Jako první krok určíme závislost velikosti zrychlení hmotného bodu na čase.
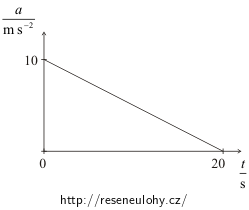
Ze zadání úlohy víme, že na počátku pohybu má hmotný bod zrychlení 10 m·s−2 a po dvaceti sekundách má nulové zrychlení. Známe tedy dva body závislosti zrychlení na čase. Protože se zrychlení má snižovat rovnoměrně, propojíme tyto dva body přímkou. Výsledný graf je na následujícím obrázku.
Rovnice přímky na obrázku je
\[a\left(t\right)\,=\,10-\frac{1}{2}t\,.\]Průběh velikosti zrychlení pro t ≤ T tedy můžeme zapsat rovnicí
\[a\left(t\right)\,=\,a_{0}\left(1-\frac{t}{T}\right)\,.\]Závislost velikosti rychlosti hmotného bodu na čase získáme integrací vztahu pro velikost zrychlení podle času:
\[v\left( t\right) \, = \, \int{a\left(t\right)\, dt} \, = \, \int{a_{0}\left(1-\frac{t}{T}\right)\, dt} \, = \, a_{0}\left(t-\frac{t^{2}}{2T}\right) \, + \, C. \]Hodnotu konstanty C určíme uvážením počáteční podmínky. Za čas t dosadíme 0 s:
\[v \left(0 \right) \, = \, 0\, \mathrm{m \cdot s^{-1}} \hspace{10px}\Rightarrow\hspace{10px}C \, = \, 0.\]Závislost velikosti rychlosti na čase je tedy dána rovnicí
\[v\left(t\right) \, = \, a_{0}\left(t-\frac{t^{2}}{2T}\right)\,.\]Konkrétní rychlost v čase T = 20 s získáme dosazením do vztahu pro velikost rychlosti:
\[v\left(T\right) \, = \, a_{0}\left(T-\frac{T^{2}}{2T}\right) \, = \, \frac{1}{2} a_{0} T \, = \, \frac{1}{2}\cdot 10 {\cdot} 20 \, \mathrm{m\, s^{-1}}= \, 100 \, \mathrm{m \cdot s^{-1}}\,. \]Závislost dráhy hmotného bodu na čase získáme integrací vztahu pro velikost rychlosti podle času:
\[x\left(t\right) \, = \, \int{v\left(t\right)\,dt}\,= \, \int{a_{0}\left(t-\frac{t^{2}}{2T}\right)\, dt}\,=\, a_{0}\left(\frac{t^{2}}{2}-\frac{t^{3}}{6T}\right) \, + \, C.\]Hodnotu konstanty C určíme uvážením počáteční podmínky. V čase t = 0 s byla i uražená dráha nulová:
\[x \left(0 \right) \, = \, 0\, \mathrm{m} \hspace{10px}\Rightarrow\hspace{10px}C \, = \, 0.\]Závislost dráhy na čase je tedy dána rovnicí
\[x\left(t\right) \, = \, a_{0}\left(\frac{t^{2}}{2}-\frac{t^{3}}{6T}\right)\,.\]Konkrétní dráhu uraženou za čas T = 20 s získáme dosazením do vztahu pro dráhu:
\[x\left(T\right) \, = \, a_{0}\left(\frac{T^{2}}{2}-\frac{T^{3}}{6T}\right) \, = \, \frac{1}{3}a_{0}T^{2}\,=\, \frac{1}{3}\cdot 10 {\cdot} 20^{2} \, \mathrm{m}\,=\, \frac{4000}{3}\, \mathrm{m}\, \dot{=}\,\] \[ \dot{=}\, 1 333{,}3 \, \mathrm{m}.\]Odpověď
Rychlost v čase T:
\[v(T)\,=\, \frac{1}{2}a_{0}T\,=\,100\,\mathrm{m \cdot s^{-1}}\,.\]Dráha ujetá za čas T:
\[x(T)\,=\,\frac{1}{3}a_{0}T^{2}\,= \, 1 333{,}3 \, \mathrm{m}\,.\]