Výška družice

Úloha číslo: 204

Vypočítejte, v jaké výšce nad rovníkem se pohybuje geostacionární družice (tj. družice, která se pohybuje stále nad stejným místem Země).

Řešte z pohledu inerciální i neinerciální vztažné soustavy.

Zápis

T = 24 h perioda rotace Země kolem své osy

Z tabulek:

κ = 6,67·10⁻¹¹ N m² kg⁻² gravitační konstanta

M = 5,97·10²⁴ kg hmotnost Země

R = 6378 km poloměr Země
Nápověda 1 – řešení z pohledu inerciální soustavy
Rozmyslete si, které síly působí na družici a co způsobují.
Řešení nápovědy 1 – z pohledu inerciální vztažné soustavy
Na úlohu se budeme dívat nejprve z hlediska inerciální soustavy.

Družice vykonává rovnoměrný pohyb po kružnici. Působí na ni pouze gravitační síla, která v tomto případě hraje zároveň roli dostředivé síly a zakřivuje trajektorii družice. Tedy gravitační a dostředivá síla se rovnají.
Nápověda 2
Napište si Newtonův gravitační zákon a vztah pro dostředivou sílu.
Řešení nápovědy 2
Newtonův gravitační zákon:
\[F_\mathrm{g} = \kappa\frac{mM}{\left( R+h\right)^{2}}\, ,\]
kde m je hmotnost družice a h je výška družice nad povrchem Země.

Dostředivá síla je rovna:
\[F_\mathrm{d} = ma_\mathrm{d} = m\frac{v^{2}}{R+h},\]
kde v je obvodová rychlost obíhání družice.

Obě tyto síly se musí rovnat, takže platí:
\[\kappa\frac{mM}{\left( R+h\right)^{2}} = m\frac{v^{2}}{R+h}.\tag{1}\]
Nápověda 3
Rozmyslete si, jakou musí mít družice rychlost, aby byla geostacionární.
Řešení nápovědy 3
Družice je geostacionární, tedy musí obíhat se stejnou úhlovou rychlostí, kterou rotuje Země. Perioda jejího oběhu musí být také stejná tedy 24 hodin.

Obvodová rychlost družice tedy je
\[v = \omega \left( R+h \right) = \frac{2\pi}{T}\left( R+h \right) ,\tag{2}\]
kde T je perioda oběhu.
Nápověda 4
Pomocí vztahů (1) a (2) vyjádřete hledanou výšku.
Řešení nápovědy 4
Obvodovou rychlost ze vztahu (2) dosadíme do rovnice (1):
\[\kappa\frac{mM}{\left( R+h \right)^{2}} = \frac{4\pi^{2}m\left( R+h\right)}{T^{2}}\, \Rightarrow \, \frac{\kappa MT^{2}}{4\pi^{2}} = \left( R+h \right)^{3}.\]

Výsledný vztah pro h je:
\[h = \sqrt[3]{\kappa\frac{MT^{2}}{4\pi^{2}}}-R.\]
Nápověda 5 – řešení z pohledu neinerciální vztažné soustavy
Rozmyslete si, jaké síly na družici působí a jaká je jejich výslednice.
Řešení nápovědy 5 – z pohledu neinerciální vztažné soustavy
Z pohledu neinerciální vztažné soustavy otáčející se spolu s družicí je družice v klidu.

Působí na ni gravitační síla a setrvačná odstředivá síla, jejich výslednice je nulová.

\[\vec{F}_\mathrm{g}\,+\,\vec{F}_\mathrm{od}\,=\,\vec{o}\]
Pro velikost sil platí:
\[F_\mathrm{g} - F_\mathrm{od} = 0,\]
tedy
\[F_\mathrm{g} = F_\mathrm{od}, \] \[F_\mathrm{g} = \kappa\frac{mM}{\left( R+h\right)^{2}}.\]
Velikost setrvačné odstředivé síly je stejná jako velikost dostředivé síly:
\[F_\mathrm{od} = m\frac{v^{2}}{R+h}.\]
Dostáváme tedy:
\[\kappa\frac{mM}{\left( R+h\right)^{2}} = m\frac{v^{2}}{R+h}.\]
Dále je řešení stejné jako v předchozí části.
Celkové řešení
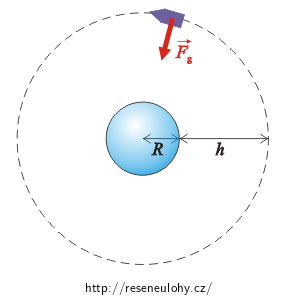
Napřed se na tuto úlohu budeme dívat z hlediska inerciálního systému.

V tomto systému je gravitační síla působící na družici silou dostředivou, která zakřivuje dráhu družice, proto:
\[F_\mathrm{g}\,=\,F_\mathrm{d}.\]
Protože ve výšce, kde létá družice, už hodnota g nebude rovna 9,81 m s⁻¹, budeme gravitační sílu počítat podle Newtonova gravitačního zákona a na pravou stranu dosadíme vztah pro dostředivou sílu
\[\kappa\frac{mM}{(R+h)^{2}}\,=\,m\frac{v^{2}}{R+h}\, ,\]
kde m je hmotnost družice, M je hmotnost Země, v je obvodová rychlost oběhu družice, R je poloměr Země a h výška družice nad povrchem Země. Nyní ještě musíme určit rychlost v.

Družice je geostacionární, tedy musí obíhat se stejnou úhlovou rychlostí, kterou rotuje Země. Perioda jejího oběhu musí být také stejná, tedy 24 hodin.

Obvodová rychlost družice tedy je
\[v = \omega \left( R+h \right) = \frac{2\pi}{T}\left( R+h \right) ,\]
kde T je perioda oběhu.

Po dosazení rychlosti do předchozího vztahu dostaneme výraz, ze kterého postupnými úpravami vyjádříme h:
\[\kappa\frac{mM}{\left( R+h \right)^{2}} = \frac{4\pi^{2}m\left( R+h\right)}{T^{2}}\, \Rightarrow \, \frac{\kappa MT^{2}}{4\pi^{2}} = \left( R+h \right)^{3}.\]

Výsledný vztah pro h je
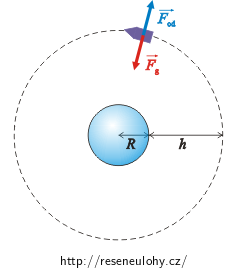
\[h = \sqrt[3]{\kappa\frac{MT^{2}}{4\pi^{2}}}-R.\]

Z pohledu neinerciální vztažné soustavy otáčející se spolu s družicí je družice v klidu.

Působí na ni gravitační síla a setrvačná odstředivá síla, jejich výslednice je nulová.

\[\vec{F}_\mathrm{g}\,+\,\vec{F}_\mathrm{od}\,=\,\vec{o}\]
Pro velikost sil platí:
\[F_\mathrm{g} - F_\mathrm{od} = 0,\]
tedy
\[F_\mathrm{g} = F_\mathrm{od}, \] \[F_\mathrm{g} = \kappa\frac{mM}{\left( R+h\right)^{2}}.\]
Velikost setrvačné odstředivé síly je stejná jako velikost dostředivé síly:
\[F_\mathrm{od} = m\frac{v^{2}}{R+h}.\]
Dostáváme tedy:
\[\kappa\frac{mM}{\left( R+h\right)^{2}} = m\frac{v^{2}}{R+h}.\]
Dále je řešení stejné jako v předchozí části.
Číselné dosazení
\[h = \sqrt[3]{\kappa\frac{MT^{2}}{4\pi^{2}}}-R = (\sqrt[3]{6{,}67{\cdot}10^{-11}\,\cdot\,\frac{5{,}97{\cdot}10^{24}\,\cdot\, \left( 86{,}4{\cdot}10^{3} \right) ^{2}}{4\pi^{2}}}-\] \[-6378{\cdot}10^{3}) \,\mathrm{m} \dot{=} 36{\cdot}10^{6}\,\mathrm{m} = 36\, 000\,\mathrm{km} \]
Odpověď
Výška družice: \[h\,=\,\sqrt[3]{\kappa\frac{MT^{2}}{4\pi^{2}}}-R.\]

Výška družice nad povrchem Země je přibližně 36 000 km.