Kotouč hozený na vodorovnou podložku
Úloha číslo: 1138
Kruhový kotouč o hmotnosti m má poloměr R a moment setrvačnosti J = mk2, kde m je hmotnost kotouče a k tzv. poloměr rotace. Neroztočený kotouč je s počáteční rychlostí v0 hozen na drsnou podložku, koeficient smykového tření je f. Určete:
- okamžik, kdy se kotouč začne pohybovat čistým valením – tj. bez smýkání,
- rychlost těžiště kotouče v tomto okamžiku,
- vzdálenost, kterou kotouč urazí do tohoto okamžiku,
- práci třecích sil (tj. změnu vnitřní energie soustavy podložka + kotouč).
Nápověda 1 (k části a.)
Ještě dříve, než se zamyslíme nad metodou řešení úlohy, si příslušnou situaci (kotouč na podložce) nakreslete. Jaké síly na kotouč působí? Vyznačte je do obrázku. Jaká je výslednice těchto sil?
Popis metody (k části a.)
Úlohu lze řešit použitím výhodného „triku“. Do těžiště kotouče přidáme ve vodorovném směru dvě síly opačného směru, obě o velikosti Ft – výše popsanou situaci tím nijak nenarušíme (neboť výslednice těchto sil i jejich výsledný moment vzhledem k těžišti jsou nulové), ale zpřehledníme ji:
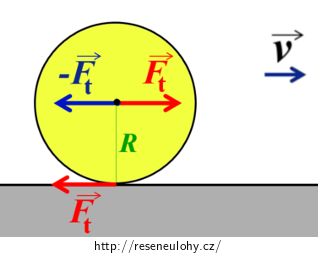
- Červeně vyznačené síly představují dvojici sil s ramenem R, které kotouč roztáčí s úhlovým zrychlením ε.
- Modře znázorněná síla umístěná v těžišti brzdí posuvný pohyb kotouče, udílí tedy záporné zrychlení a.
Z těchto dvou zrychlení jsme schopni určit vývoj úhlové rychlosti otáčení kotouče ω(t) a vývoj rychlosti posuvného pohybu těžiště kotouče v(t).
Jaké kritérium pak rozhodne, ve kterém čase t1 se začne kotouč odvalovat bez smýkání? V takovém okamžiku bude muset platit:
\[v(t_1)\,=\,R\omega(t_1).\tag{1}\]Tato podmínka charakterizuje rotační pohyb bez prokluzování či smýkání.
Nápověda 2 (k části a.) – úhlové zrychlení ε
Nejdříve určíme úhlové zrychlení, kterým červeně znázorněná dvojice sil roztáčí kotouč. Umíte určit toto zrychlení, znáte-li moment této dvojice a také moment setrvačnosti kotouče? Pomoci by vám měla 2. věta impulsová (ve tvaru pro rotaci kolem pevné osy), znalost momentu dvojice sil a výpočet třecí síly.
Nápověda 3 (k části a.) – úhlová rychlost ω = ω(t)
Integrací úhlového zrychlení dostanete časový vývoj úhlové rychlosti. Proveďte výpočet a nezapomeňte dopočítat integrační konstantu.
Nápověda 4 (k části a.) – zrychlení posuvného pohybu a
Právě jsme vyřešili rotační pohyb kotouče, zaměříme se nyní na jeho posuvný pohyb. Pomocí 2. Newtonova zákona určete zrychlení a, které uděluje kotouči modře znázorněná síla −Ft v obrázku výše.
Nápověda 5 (k části a.) – rychlost posuvného pohybu v = v(t)
Také časový vývoj rychlosti posuvného pohybu těžiště kotouče určíme integrací, tentokrát integrací zrychlení a. Opět pečlivě hlídejte integrační konstanty.
Nápověda 6 (k části a.)
Předcházejícími výpočty jsme vyjádřili časový průběh úhlové rychlosti i rychlosti posuvného pohybu těžiště kotouče, nyní tedy můžeme tyto průběhy dosadit do podmínky (1) a vyjádřit hledaný čas t1.
Nápověda 7 (k části b.)
Nyní určete rychlost těžiště posuvného pohybu kotouče v dopočítaném čase t1. Uvědomte si, že víte, jak se rychlost s časem mění.
Nápověda 8 (k části c.)
Ve třetím úkolu máme určit dráhu x, kterou kotouč urazí od počátku pohybu do doby t1. Je dobré si uvědomit, že známe časový vývoj rychlosti v kotouče. Jakým způsobem v případě obecného pohybu určujeme dráhu ze známého průběhu rychlosti? Příslušnou metodu použijte a dopočítejte dráhu x.
Nápověda 9 (k části d.)
Práci třecích sil, kterou chceme na závěr určit, můžeme chápat jako přírůstek vnitřní energie ΔU soustavy podložka + kotouč. Jaké veličiny potřebujeme znát, abychom mohli tento přírůstek dopočítat? Použijte zákon zachování energie a vyjádřete ΔU.
Nápověda 10 (k části d.)
Vyjádřete energie ve vztahu (15) a dopočítejte přírůstek vnitřní energie soustavy podložka + kotouč (tj. práci třecích sil).
Celkové řešení
Část a.
Na kotouč pohybující se po vhození po podložce působí:
- tíhová síla FG svisle dolů,
- tlaková síla podložky R svisle vzhůru,
- třecí síla Ft ve vodorovném směru proti pohybu.
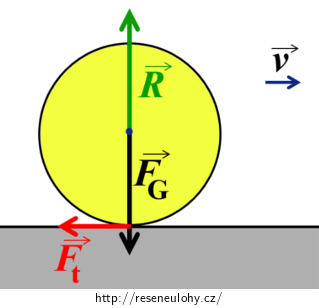
Protože poloha kotouče se ve svislém směru nemění (kotouč nikam „nevyskakuje“ ani se nikam „nepropadá“), musí být výslednice tíhové a tlakové síly nulová (dále už tyto síly nebudeme do obrázků kreslit). Třecí síla se naopak zjevně s žádnou silou neruší a brzdí pohyb kotouče.
Úlohu lze řešit použitím výhodného „triku“. Do těžiště kotouče přidáme ve vodorovném směru dvě síly opačného směru, obě o velikosti Ft – výše popsanou situaci tím nijak nenarušíme (neboť výslednice těchto sil i jejich výsledný moment vzhledem k těžišti jsou nulové), ale zpřehledníme ji:

- Červeně vyznačené síly představují dvojici sil s ramenem R, které kotouč roztáčí s úhlovým zrychlením ε.
- Modře znázorněná síla umístěná v těžišti brzdí posuvný pohyb kotouče, udílí tedy záporné zrychlení a.
Z těchto dvou zrychlení jsme schopni určit vývoj úhlové rychlosti otáčení kotouče ω(t) a vývoj rychlosti posuvného pohybu těžiště kotouče v(t). V okamžiku, kdy se začne kotouč odvalovat bez smýkání, bude muset platit:
\[v(t_1)\,=\,R\omega(t_1).\tag{1}\]Tato podmínka charakterizuje rotační pohyb bez prokluzování či smýkání.
Výpočet průběhu úhlové rychlosti:Úhlové zrychlení ε určíme z pohybové rovnice pro rotační pohyb (jde o tvar 2. věty impulsové přepsané pro případ rotace kolem pevné osy):
\[M\,=\,J\varepsilon\,\Rightarrow\,\varepsilon\,=\,\frac{M}{J},\tag{2}\]kde M je moment příslušné dvojice sil Ft a J moment setrvačnosti kotouče. Ze znalosti práce s momentem dvojice sil M a vztahu pro velikost třecí síly Ft dostáváme:
\[M\,=\,F_\mathrm{t}R\,=\,F_\mathrm{G}fR\,=\,mgfR,\tag{3}\]kde R je poloměr kotouče, m jeho hmotnost, g tíhové zrychlení a f součinitel smykového tření. Ze zadání známe moment setrvačnosti kotouče J, který spolu se vztahem (3) dosadíme do rovnice (2):
\[\varepsilon\,=\,\frac{M}{J}\,=\,\frac{mgfR}{mk^2}\,=\,\frac{gfR}{k^2}.\tag{4}\]Závislost úhlové rychlosti na čase získáme z úhlového zrychlení dopočteného ve vztahu (4) integrací:
\[\omega(t)\,=\,\int\varepsilon(t)dt\,=\,\int{\frac{gfR}{k^2}dt}\,=\,\frac{gfR}{k^2}t\,+\,c_1,\tag{5}\] kde c1 je integrační konstanta. Z okrajové podmínky ω(0) = 0 (tj. v okamžiku vhození kotouče na podložku kotouč nerotoval) dostáváme c1 = 0, tedy: \[\omega(t)\,=\,\frac{gfR}{k^2}t.\tag{6}\]Úhlová rychlost tedy lineárně roste.
Výpočet průběhu rychlosti posuvného pohybu:Podle 2. Newtonova zákona platí:
\[-F_\mathrm{t}\,=\,ma\,\Rightarrow\,a\,=\,-\frac{F_\mathrm{t}}{m}.\tag{7}\]Do rovnice (7) snadno dosadíme již použitý vztah pro velikost třecí síly:
\[a\,=\,-\frac{F_\mathrm{G}f}{m}\,=\,-\frac{mgf}{m}\,=\,-gf.\tag{8}\]Závislost rychlosti posuvného pohybu na čase získáme ze zrychlení a dopočteného ve vztahu (6) integrací:
\[v(t)\,=\,\int{a(t)}dt\,=\,-\int{gf}dt\,=\,-gft\,+\,c_2,\tag{9}\]kde c2 je integrační konstanta. Z okrajové podmínky v(0) = v0 (tato podmínka se vyskytuje v zadání úlohy) dostáváme c2 = v0, tedy:
\[v(t)\,=\,v_0\,-\,gft.\tag{10}\]Rychlost posuvného pohybu těžiště kotouče tedy lineárně klesá.
Dosazením vztahů (6) a (10) do rovnice (1) pro čas t1 dostáváme:
\[v(t_1)\,=\,R\omega(t_1),\] \[v_0\,-\,gft_1\,=\,R\frac{gfR}{k^2}t_1,\] \[v_0\,=\,gft_1(1\,+\,\frac{R^2}{k^2}),\] \[t_1\,=\,\frac{v_0}{gf(1\,+\,\frac{R^2}{k^2})}.\tag{11}\]Část b.
Rychlost posuvného pohybu těžiště v čase t1 vypočítáme velmi snadno ze vztahu (10), kde jsme určili rychlost v jako funkci času. Pro t = t1 s použitím vztahu (11) platí:
\[v_1\,=\,v(t_1)\,=\,v_0\,-\,gft_1\,=\,v_0\,-\,\frac{gfv_0}{gf(1\,+\,\frac{R^2}{k^2})}\,=\,\frac{v_0}{1\,+\,\frac{k^2}{R^2}}.\tag{12}\]
Část c.
Známe-li časový vývoj rychlosti v = v(t), spočítáme uraženou dráhu jako určitý integrál z v = v(t) od počátku pohybu (t0 = 0 sekund) do okamžiku vymezeného časem t1:
\[x\,=\,\int_0^{t_1}{v(t)dt}\,=\,\int_0^{t_1}{(v_0\,-\,gft)dt}\,=\,[v_0t\,-\,\frac{1}{2}gft^2]_0^{t_1}\,=\] \[=\,v_0t_1\,-\,\frac{1}{2}gft_1^2.\tag{13}\]Za čas t1 nyní dosadíme ze vztahu (11):
\[x\,=\,v_0\frac{v_0}{gf(1\,+\,\frac{R^2}{k^2})}\,-\,\frac{1}{2}gf(\frac{v_0}{gf(1\,+\,\frac{R^2}{k^2})})^2\] \[=\,\frac{2v_0^2gf(1\,+\,\frac{R^2}{k^2})\,-\,v_0^2gf}{2g^2f^2(1\,+\,\frac{R^2}{k^2})^2}\,=\,\frac{v_0^2}{2gf}\frac{1\,+\,\frac{2R^2}{k^2}}{(1\,+\,\frac{R^2}{k^2})^2}.\tag{14}\]Část d.
Práci třecích sil můžeme chápat jako přírůstek vnitřní energie ΔU soustavy kotouč + podložka. Tento přírůstek můžeme vyjádřit jako rozdíl kinetické energie kotouče na počátku pohybu (tj. v čase t0 = 0 sekund) a v čase t1. Pohyb probíhá ve vodorovné rovině, potenciální energie kotouče se nemění. Platí tedy:
\[W\,=\,{\Delta}U\,=\,E_\mathrm{k1}\,-\,E_\mathrm{k2},\tag{15}\]kde Ek1 je kinetická energie kotouče na počátku pohybu a Ek2 kinetická energie kotouče v čase t1.
Kinetická energie kotouče na počátku pohybu je reprezentována pouze energií posuvného pohybu:
\[E_\mathrm{k1}\,=\,\frac{1}{2}mv_0^2.\tag{16}\]V čase t1 je kinetická energie kotouče složena z energie posuvného a rotačního pohybu:
\[E_\mathrm{k2}\,=\,\frac{1}{2}mv_1^2\,+\,\frac{1}{2}J{\omega_1^2},\tag{17}\]kde ω1 je úhlová rychlost v čase t1, kterou můžeme vyjádřit ze vztahů (6) a (11) jako:
\[{\omega}_1\,=\,\frac{gfR}{k^2}t_1\,=\,\frac{gfR}{k^2}\frac{v_0}{gf(1\,+\,\frac{R^2}{k^2})}\,=\,\frac{Rv_0}{ k^2\,+\,R^2}.\tag{18}\]Dosazením vztahů (16) až (18) do rovnice (15) dostáváme:
\[W\,=\,\frac{1}{2}mv_0^2\,-\,\frac{1}{2}m(\frac{v_0}{1\,+\,\frac{k^2}{R^2}})^2\,-\,\frac{1}{2}mk^2(\frac{Rv_0}{ k^2\,+\,R^2})^2\] \[=\,\frac{1}{2}mv_0^2(1\,-\,\frac{1}{(\frac{k^2\,+\,R^2}{R^2})^2}\,-\,\frac{k^2R^2}{(k^2\,+\,R^2)^2})\] \[=\,\frac{1}{2}mv_0^2(\frac{(k^2\,+\,R^2)^2\,-\,R^4\,-\,k^2R^2}{(k^2\,+\,R^2)^2})\,=\,\frac{1}{2}mv_0^2\frac{k^2}{ k^2\,+\,R^2}\] \[=\,\frac{1}{2}mv_0^2\frac{1}{1\,+\,\frac{R^2}{k^2}}.\tag{19}\]Alternativní řešení části d.
Jiný způsob, jak vyřešit část d., vychází přímo ze vztahu pro výpočet mechanické práce třecí síly:
\[W\,=\,F_\mathrm{t}s\,=\,F_\mathrm{G}fs\,=\,mgfs,\tag{20}\]kde s je dráha, kterou kotouč po podložce urazil smýkáním. Tuto dráhu určíme jako rozdíl celkové uražené dráhy x a dráhy uražené valením x0:
\[s\,=\,x\,-\,x_0.\tag{21}\]Celkovou uraženou dráhu jsme vyjádřili ve vztahu (14), dráhu x0 uraženou valením vypočítáme jako součin poloměru kotouče R a celkového „odvaleného“ úhlu φ(t1):
\[x_0\,=\,R\varphi(t_1).\tag{22}\]Celkový odvalený úhel získáme integrací vztahu (6) pro úhlovou rychlost:
\[\varphi(t_1)\,=\,\int_0^{t_1}\omega(t)dt\,=\,\int_0^{t_1}\frac{gfR}{k^2}tdt\,=\,\frac{gfR}{2k^2}t_1^2.\tag{23}\]Spojením vztahů (11), (14) a (20) až (23) dostáváme pro práci třecích sil:
\[W\,=\,mgf(\frac{v_0^2}{2gf}\frac{1\,+\,\frac{2R^2}{k^2}}{(1\,+\,\frac{R^2}{k^2})^2}\,-\,R\frac{gfR}{2k^2}(\frac{v_0}{gf(1\,+\,\frac{R^2}{k^2})})^2)\] \[=\,mgf\frac{v_0^2}{2gf}\frac{1}{(1\,+\,\frac{R^2}{k^2})^2}(1\,+\,\frac{2R^2}{k^2}\,-\,\frac{R^2}{k^2})\,=\,\frac{1}{2}mv_0^2\frac{1}{1\,+\,\frac{R^2}{k^2}}.\]Odpověď
Část a:
Kotouč se začne pohybovat čistým valením bez tření v čase t1 od počátku pohybu:
\[t_1\,=\,\frac{v_0}{gf(1\,+\,\frac{R^2}{k^2})}.\]Část b:
Rychlost posuvného pohybu těžiště kotouče bude v tuto chvíli rovna v1:
\[v_1\,=\,\frac{v_0}{1\,+\,\frac{k^2}{R^2}}.\]
Část c:
Dráha, kterou kotouč od počátku pohybu urazil, bude ve stejnou chvíli rovna x:
\[x\,=\,\frac{v_0^2}{2gf}\frac{1\,+\,\frac{2R^2}{k^2}}{(1\,+\,\frac{R^2}{k^2})^2}.\]Část d:
Třecí síly během tohoto děje vykonaly práci W:
\[W\,=\,\frac{1}{2}mv_0^2\frac{1}{1\,+\,\frac{R^2}{k^2}}.\]


