Brzdící automobil
Úloha číslo: 94
Automobil, který jede rychlostí 80 km·h−1, zastaví při maximálním sešlápnutí brzdového pedálu na vodorovné asfaltové silnici na dráze 50 m. Jaká bude jeho brzdná dráha na stejné vozovce, která svírá s vodorovnou rovinou úhel 5°? Uvažujte jak případ, kdy brzdí při jízdě z kopce, tak do kopce. Předpokládejte, že v čase t = 0 s byla souřadnice x = 0 m. V žádném z uvedených případů nedojde ke smyku kol. Odpor vzduchu neuvažujte.
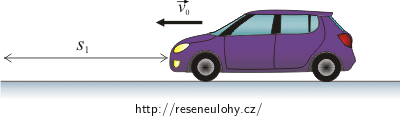
Rozbor
Z informací v zadání nejprve zjistíme, jak velká brzdná síla působí na auto při brzdění na rovině. Nedochází-li ke smyku kol, je brzdná síla realizovaná jednak valivým odporem kol (pro který platí \(F_\mathrm{v}\,=\,\xi\frac{N_\mathrm{k}}{R}\), R je poloměr kol auta, ξ [čtěte „ksí“] je rameno valivého odporu, Nk je tlaková síla, kterou působí kolo na silnici) a jednak klidovým třením kol o vozovku (rychlost kola je v místě dotyku vzhledem k vozovce nulová). Budeme předpokládat, že při maximálním sešlápnutí brzdového pedálu bude auto na hranici smyku a bude se realizovat maximální klidová třecí síla \(F_\mathrm{t}\,=\,fN\). Valivý odpor nebudeme uvažovat (hodnota ξ je pro gumu a asfalt rovna 0,0016 m a hodnota f je rovna 0,55). Dále je třeba se zamyslet, zda a jak se brzdná síla změní při brzdění z kopce a do kopce.
Zápis
v0 = 80 km·h−1 rychlost auta s1 = 50 m brzdná dráha pro auto jedoucí po vodorovné silnici α = 5° úhel, který svírá vozovka s vodorovnou rovinou sz1 = ? m brzdná dráha pro auto jedoucí do kopce sz2 = ? m brzdná dráha pro auto jedoucí z kopce Nápověda 1 – brzdění na rovině – zrychlení auta
Nakreslete si obrázek, vyznačte síly působící na auto a napište pro něj pohybovou rovnici. Z ní vyjádřete zrychlení auta.
Nápověda 2 – brzdění na rovině – brzdná síla
Znáte zrychlení auta. Vyjádřete, jak se s časem mění jeho rychlost a souřadnice. Zjistěte čas a dráhu zastavení.
Poznámka
K vyjádření brzdné síly můžeme využít i zákon zachování energie. Kinetická energie auta na začátku brzdění je rovna práci brzdné síly na brzdné dráze:
\[W\,=\,E_\mathrm{k}\,,\] \[F_\mathrm{t}s_\mathrm{z}\,=\,\frac{mv_0^2}{2}.\]Odtud:
\[F_\mathrm{t}=\frac{mv_0^2}{2s_\mathrm{z}}\,.\]Nápověda 3 – brzdná síla na rovině a na svahu
Brzdná síla je realizovaná maximálním klidovým třením mezi koly auta a silnicí. Uvědomte si, na čem třecí síla závisí a zda se bude lišit její velikost při brzdění na rovině a na svahu.
Nápověda 4 – brzdění do kopce – pohybové rovnice
Uvědomte si, jaké síly působí na auto jedoucí do kopce. Nakreslete si obrázek a síly do něj vyznačte. Napište pohybovou rovnici pro auto a přepište ji skalárně.
Nápověda 5 – brzdná síla na svahu
Brzdná síla na svahu je, stejně jako na rovině, realizovaná klidovým třením mezi koly auta a silnicí. Vyjádřete třecí sílu pro případ auta jedoucího do kopce, vyjádřete ji také pomocí f ze vztahu (12).
Nápověda 6 – vyjádření zrychlení, výpočet ujeté vzdálenosti
Z pohybové rovnice (13) vyjádřete zrychlení auta. Obdobně jako v případě jízdy po rovině vyjádřete brzdnou dráhu auta.
Nápověda 7 – brzdění z kopce – pohybové rovnice
Uvědomte si, jaké síly působí na auto jedoucí z kopce. Nakreslete si obrázek a síly do něj vyznačte. Napište pohybovou rovnici pro auto a přepište ji skalárně.
Nápověda 8 – brzdná síla na svahu
Brzdná síla na svahu je, stejně jako na rovině, realizovaná klidovým třením mezi koly auta a silnicí. Vyjádřete třecí sílu pro případ auta jedoucího z kopce. Vyjádřete ji také pomocí f ze vztahu (12).
Nápověda 9 – vyjádření zrychlení, výpočet ujeté vzdálenosti
Z pohybové rovnice (23) vyjádřete zrychlení auta. Obdobně jako v případě jízdy po rovině vyjádřete brzdnou dráhu auta.
CELKOVÉ ŘEŠENÍ
Brzdění na rovině
Síly působící na auto:
\(\vec{F}_\mathrm{G}\)…síla tíhová
\(\vec{N}\)…normálová síla, kterou na auto působí silnice (sílu \(\vec{N}\) označujeme jako výslednici sil působících na všechna kola auta)
\(\vec{F}_\mathrm{t}\)…brzdná síla
Pohybová rovnice:
\[\vec{F}_\mathrm{t}+\vec{F}_\mathrm{G}+\vec{N}\,=\, m\vec{a}\,.\]Pohybovou rovnici přepíšeme skalárně. Zvolíme soustavu souřadnic, kde osa x míří ve směru pohybu auta. Osa y je kolmá na osu x:
\[x:\qquad -F_\mathrm{t}\,=\,ma,\tag{1}\] \[y:\qquad N-F_\mathrm{G}\,=\,0.\tag{2}\]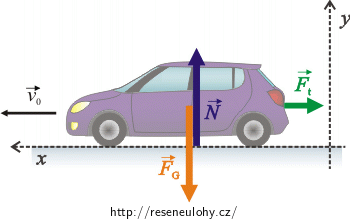
Zrychlení auta vyjádříme z rovnice (1):
\[a\,=\,-\frac{F_\mathrm{t}}{m}\,.\tag{3}\]Výpočet v(t) a s(t):
Integrací vztahu (3) získáme závislost rychlosti auta na čase:
\[v(t)\,=\,\int{a(t)}\,\mathrm{d}t\,,\] \[v(t)\,=\,\int{\left(-\frac{F_\mathrm{t}}{m}\right)}\,\mathrm{d}t,\] \[v(t)\,=\,-\frac{F_\mathrm{t}}{m}t\,+\,K.\tag{4}\]K je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla rychlost v = v0. Dosadíme-li t = 0 s do vztahu (4), pak musí platit:
v0 = 0 + K.
A tedy:
v0 = K.
Přepíšeme-li rovnici (4), získáme závislost rychlosti auta na čase:
\[v(t)\,=\,-{\frac{F_\mathrm{t}}{m}}t\,+\,v_0\,.\tag{5}\]Integrací vztahu (5) získáme závislost souřadnice na čase:
\[x(t)\,=\,\int{v(t)}\,\mathrm{d}t\,,\] \[x(t)\,=\,\int{\left(-\frac{F_\mathrm{t}}{m}t\,+\,v_0\right)}\,\mathrm{d}t,\] \[x(t)\,=\,-\frac{F_\mathrm{t}}{2m}t^2\,+\,v_0t\,+\,C.\tag{6}\]C je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla souřadnice x = 0. Dosadíme-li t = 0 s do vztahu (6), pak musí platit:
C = 0.
Přepíšeme-li rovnici (6), získáme závislost souřadnice auta na čase:
\[x(t)\,=\,-{\frac{F_\mathrm{t}}{2m}}t^2\,+\,v_0t\,.\tag{7}\]Výpočet času a dráhy zastavení:
V okamžiku zastavení je rychlost auta nulová, čas zastavení tz spočteme dosazením nulové rychlosti do vztahu (5):
\[0\,=\,-{\frac{F_\mathrm{t}}{m}}t_\mathrm{z}\,+\,v_0\,,\] \[t_\mathrm{z}\,=\,\frac{mv_0}{F_\mathrm{t}}.\tag{8}\]Dráhu zastavení sz spočteme dosazením času zastavení tz do vztahu (7):
\[s_\mathrm{z}\,=\,-{\frac{F_\mathrm{t}}{2m}}t_\mathrm{z}^2\,+\,v_0t_\mathrm{z}\,,\] \[s_\mathrm{z}\,=\,-{\frac{F_\mathrm{t}}{2m}}\left(\frac{mv_0}{F_\mathrm{t}}\right)^2\,+\,v_0\frac{mv_0}{F_\mathrm{t}},\] \[s_\mathrm{z}\,=\,-\frac{mv_0^2}{2F_\mathrm{t}}\,+\,\frac{mv_0^2}{F_\mathrm{t}},\] \[s_\mathrm{z}\,=\,\frac{mv_0^2}{2F_t}.\tag{9}\]Ze vztahu (9) vyjádříme brzdnou sílu:
\[F_\mathrm{t}\,=\,\frac{mv_0^2}{2s_\mathrm{z}}\,.\tag{10}\]Poznámka:
K vyjádření brzdné síly můžeme využít i zákon zachování energie. Kinetická energie auta na začátku brzdění je rovna práci brzdné síly na brzdné dráze:
\[W\,=\,E_\mathrm{k}\,,\] \[F_\mathrm{t}s_\mathrm{z}\,=\,\frac{mv_0^2}{2}.\]Odtud:
\[F_\mathrm{t}=\frac{mv_0^2}{2s_\mathrm{z}}\,.\]Třecí síla je dána vztahem:
\[F_\mathrm{t}\,=\,fN,\]f…koeficient klidového tření
N…tlaková síla, kterou působí auto na silnici
Je vidět, že třecí síla závisí na kolmé tlakové síle N působící mezi silnicí a koly auta. Ta bude na rovině a na svahu odlišná.
Na rovině platí:
\[F_\mathrm{t}\,=\,fN\,=\,fmg\,.\tag{11}\]Koeficient tření f bude na rovině i na svahu stejný. Vyjádříme ho z rovnice (11):
\[f\,=\,\frac{F_\mathrm{t}}{mg}\,.\]Dosadíme za Ft ze vztahu (10):
\[f\,=\,\frac{v_0^2}{2gs_\mathrm{z}}\,.\tag{12}\]Brzdění do kopce
Síly působící na auto jedoucí do kopce:
\(\vec{F}_\mathrm{G}\)…síla tíhová
\(\vec{N}_1\)…tlaková síla, kterou na auto působí silnice
\(\vec{F}_\mathrm{t_1}\)…brzdná síla
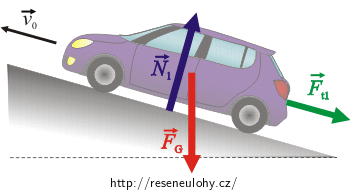
Pohybová rovnice pro auto jedoucí do kopce:
\[\vec{F}_\mathrm{t_1}+\vec{F}_\mathrm{G}+\vec{N}_1\,=\, m\vec a_1.\]Pohybovou rovnici přepíšeme skalárně, zvolíme soustavu souřadnic, kde osa x míří ve směru pohybu auta. Osa y je kolmá na osu x. Tíhovou sílu rozložíme do směru osy x a y:
\[F_\mathrm{G_x}\,=\,F_\mathrm{G}\sin\alpha,\] \[F_\mathrm{G_y}\,=\,F_\mathrm{G}\cos\alpha.\]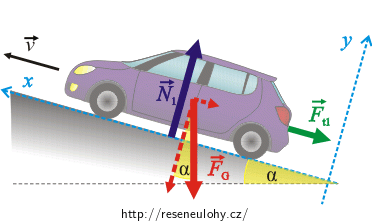
Pohybová rovnice skalárně:
\[x:\qquad -F_\mathrm{t_1}-F_\mathrm{G}\sin\alpha\,=\, ma_1,\tag{13}\] \[y:\qquad N_1-F_\mathrm{G}\cos\alpha\,=\,0.\tag{14}\]Na svahu platí:
\[F_\mathrm{t_1}\,=\,fN_1\,.\]Ze vztahu (14) vyjádříme sílu N1 a dosadíme:
\[F_\mathrm{t_1}\,=\,fF_\mathrm{G}\cos\alpha\,.\]Dosadíme za f ze vztahu (12):
\[F_\mathrm{t_1}\,=\,\frac{v_0^2}{2gs_\mathrm{z}}mg\cos\alpha\,=\, \frac{v_0^2m\cos\alpha}{2s_\mathrm{z}}\,.\tag{15}\]Z rovnice (13) vyjádříme zrychlení:
\[-F_\mathrm{t_1}-mg\sin\alpha\,=\, ma_1\,,\] \[-\frac{F_\mathrm{t_1}}{m}-g\sin\alpha\,=\, a_1.\tag{16}\]Výpočet ujeté vzdálenosti pro auto jedoucí do kopce:
Integrací zrychlení získáme závislost rychlosti na čase:
\[v_1(t)\,=\,\int{a_1(t)}\,\mathrm{d}t\,,\] \[v_1(t)\,=\,\int{\left(-\frac{F_\mathrm{t_1}}{m}-g\sin\alpha\right)}\mathrm{d}t,\] \[v_1(t)\,=\,-\frac{F_\mathrm{t_1}}{m}t-gt\sin\alpha+K.\tag{17}\]K je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla rychlost v = v0. Dosadíme-li t = 0 s do vztahu (17), pak musí platit:
v0 = 0 + K.
A tedy:
v0 = K.
Přepíšeme-li rovnici (17), získáme závislost rychlosti auta na čase:
\[v_1(t)\,=\,-\frac{F_\mathrm{t_1}}{m}t-gt\sin\alpha+v_0\,.\tag{18}\]Integrací vztahu (18) získáme závislost souřadnice na čase:
\[x_1(t)\,=\,\int{v_1(t)}\,\mathrm{d}t\,,\] \[x_1(t)\,=\,\int{\left(-\frac{F_\mathrm{t_1}}{m}t-gt\sin\alpha+v_0\right)}\,\mathrm{d}t,\] \[x_1(t)\,=\,-\frac{F_\mathrm{t_1}}{2m}t^2-\frac{gt^2}{2}\sin\alpha+v_0t+C.\tag{19}\]C je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla souřadnice x = 0. Dosadíme-li t = 0 s do vztahu (19), pak musí platit:
C = 0.
Přepíšeme-li rovnici (19), získáme závislost souřadnice auta na čase:
\[x_1(t)\,=\,-\frac{F_\mathrm{t_1}}{2m}t^2-\frac{gt^2}{2}\sin\alpha+v_0t\,.\tag{20}\]Čas zastavení tz1 spočteme dosazením nulové rychlosti do vztahu (18):
\[0\,=\,-\frac{F_\mathrm{t_1}}{m}t_\mathrm{z_1}-gt_\mathrm{z_1}\sin\alpha+v_0\,,\] \[v_0\,=\,t_\mathrm{z_1}\left(\frac{F_\mathrm{t_1}}{m}+g\sin\alpha\right),\]\[t_\mathrm{z_1}\,=\,\frac{v_0}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha}.\tag{21}\]
Čas tz1 dosadíme do vztahu (20) a spočteme ujetou vzdálenost sz1:
\[s_\mathrm{z_1}\,=\,-\frac{F_\mathrm{t_1}}{2m}t_\mathrm{{z_{1}}}^2- \frac{g{t_\mathrm{z_1}}^2}{2}\sin\alpha+v_0 t_\mathrm{z_1}\,,\] \[s_\mathrm{z_1}\,=\,-\frac{F_\mathrm{t_1}}{2m}\left(\frac{v_0}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha}\right)^2 -\frac{g\left(\frac{v_0}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha}\right)^2}{2}\sin\alpha +v_0\frac{v_0}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha},\] \[s_\mathrm{z_1}\,=\,-\frac{\frac{F_\mathrm{t_1}}{m}v_0^2}{2\left(\frac{F_\mathrm{t_1}}{m}+g\sin\alpha\right)^2} -\frac{gv_0^2\sin\alpha}{2\left(\frac{F_\mathrm{t_1}}{m}+g\sin\alpha\right)^2} +\frac{v_0^2}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha},\] \[s_\mathrm{z_1}\,=\,-\frac{v_0^2\left(\frac{F_\mathrm{t_1}}{m}+g\sin\alpha\right)}{2\left(\frac{F_{t_1}}{m}+g\sin\alpha\right)^2} +\frac{v_0^2}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha},\] \[s_\mathrm{z_1}\,=\,-\frac{v_0^2}{2\left(\frac{F_\mathrm{t_1}}{m}+g\sin\alpha\right)} +\frac{v_0^2}{\frac{F_\mathrm{t_1}}{m}+g\sin\alpha} \,=\,\frac{v_0^2}{2\left(\frac{F_\mathrm{t_1}}{m}+g\sin\alpha\right)}.\]Dosadíme za Ft1 ze vztahu (15):
\[s_\mathrm{z_1}\,=\,\frac{v_0^2} {2\left(\frac{\frac{v_0^2m\cos\alpha}{2s_\mathrm{z}}}{m}+g\sin\alpha\right)} \,=\,\frac{v_0^2}{2\left(\frac{v_0^2\cos\alpha}{2s_\mathrm{z}}+g\sin\alpha\right)}\,,\] \[s_\mathrm{z_1}\,=\,\frac{s_\mathrm{z}v_0^2}{v_0^2\cos\alpha+2s_\mathrm{z}g\sin\alpha}.\tag{22}\]Do vztahu (22) dosadíme číselně:
\[s_\mathrm{z_1}\,=\,\frac{50\left(\frac{80}{3{,}6}\right)^2}{\left(\frac{80}{3{,}6}\right)^2 \cos{5^{\circ}}\,+\,2\,\cdot50\,\cdot9{,}81\sin 5^{\circ}}\,\mathrm{m}\,,\] \[s_\mathrm{z_1}\,=\,\frac{50\,\cdot22{,}22^2}{22{,}22^2\cdot\,0{,}997\, +\,981\,\cdot\,0{,}087}\,\mathrm{m},\] \[s_\mathrm{z_1}\,=\,\frac{50\,\cdot\,493{,}72}{493{,}72\,\cdot\,0{,}997\,+\,85{,}35}\,\mathrm{m}\,=\, \frac{24\,612}{492{,}24\,+\,85{,}35}\,\mathrm{m}, \] \[s_\mathrm{z_1}\,=\,\frac{24\,612}{577{,}59}\,\mathrm{m}\,=\,42{,}61\,\mathrm{m}\,\dot=\,42{,}6\,\mathrm{m}.\]Brzdění z kopce
Síly působící na auto jedoucí z kopce:
\(\vec{F}_\mathrm{G}\)…síla tíhová
\(\vec{N}_2\)…tlaková síla, kterou na auto působí silnice
\(\vec{F}_\mathrm{t_2}\)…brzdná síla
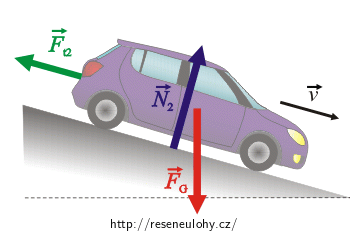
Pohybová rovnice pro auto jedoucí z kopce:
\[\vec{F}_\mathrm{t_2}+\vec{F}_\mathrm{G}+\vec{N}_2\,=\, m\vec a_2.\]Pohybovou rovnici přepíšeme skalárně, zvolíme soustavu souřadnic, kde osa x míří ve směru pohybu auta. Osa y je kolmá na osu x. Tíhovou sílu rozložíme do směru osy x a y:
\[F_\mathrm{{G}_x}\,=\,F_\mathrm{G}\sin\alpha,\] \[F_\mathrm{{G}_y}\,=\,F_\mathrm{G}\cos\alpha.\]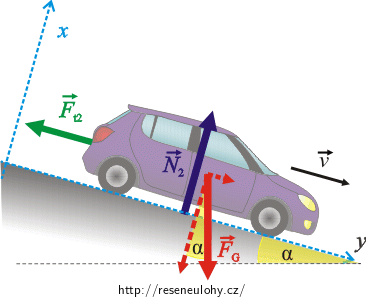
Pohybová rovnice skalárně:
\[x:\qquad -F_{t_2}+F_\mathrm{G}\sin\alpha\,=\, ma_2,\tag{23}\] \[y:\qquad N_2-F_\mathrm{G}\cos\alpha\,=\,0.\tag{24}\]Na svahu platí:
\[F_\mathrm{t_2}\,=\,fN_2.\]Ze vztahu (24) vyjádříme sílu N2 a dosadíme:
\[F_\mathrm{t_2}\,=\,fF_\mathrm{G}\cos\alpha\,.\]Dosadíme za f ze vztahu (12):
\[F_\mathrm{t_2}\,=\,\frac{v_0^2}{2gs_\mathrm{z}}mg\cos\alpha\,=\, \frac{v_0^2m\cos\alpha}{2s_\mathrm{z}}\,.\tag{25}\]Poznámka: Vztahy (15) a (25) jsou stejné, třecí síla z kopce i do kopce na stejném svahu je stejná.
Z rovnice (23) vyjádříme zrychlení:
\[-F_\mathrm{t_2}+mg\sin\alpha\,=\, ma_2,\] \[-\frac{F_\mathrm{t_2}}{m}+g\sin\alpha\,=\, a_2.\tag{26}\]Výpočet ujeté vzdálenosti pro auto jedoucí z kopce:
Integrací zrychlení získáme závislost rychlosti na čase:
\[v_2(t)\,=\,\int{a_2(t)}\,\mathrm{d}t\,,\] \[v_2(t)\,=\,\int{\left(-\frac{F_\mathrm{t_2}}{m}+g\sin\alpha\right)}\,\mathrm{d}t,\]\[v_2(t)\,=\,-\frac{F_{t_2}}{m}t+gt\sin\alpha+L.\tag{27}\]
L je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla rychlost v = v0. Dosadíme-li t = 0 s do vztahu (27), pak musí platit:
v0 = 0 + L.
A tedy:
v0 = L.
Přepíšeme-li rovnici (27), získáme závislost rychlosti auta na čase:
\[v_2(t)\,=\,-\frac{F_\mathrm{t_2}}{m}t+gt\sin\alpha+v_0\,.\tag{28}\]Integrací vztahu (28) získáme závislost souřadnice na čase:
\[x_2(t)\,=\,\int{v_2(t)}\,\mathrm{d}t\,,\] \[x_2(t)\,=\,\int{\left(-\frac{F_\mathrm{t_2}}{m}t+gt\sin\alpha+v_0\right)}\,\mathrm{d}t,\]\[x_2(t)\,=\,-\frac{F_{t_2}}{2m}t^2+\frac{gt^2}{2}\sin\alpha+v_0t+D.\tag{29}\]
D je konstanta, kterou určíme z počátečních podmínek:
V čase t = 0 s byla souřadnice x = 0. Dosadíme-li t = 0 s do vztahu (29), pak musí platit:
D = 0.
Přepíšeme-li rovnici (29), získáme závislost souřadnice auta na čase:
\[x_2(t)\,=\,-\frac{F_\mathrm{t_2}}{2m}t^2+\frac{gt^2}{2}\sin\alpha+v_0t\,.\tag{30}\]Čas zastavení tz2 spočteme dosazením nulové rychlosti do vztahu (28):
\[0\,=\,-\frac{F_\mathrm{t_2}}{m}t_\mathrm{z_2}+gt_\mathrm{z_2}\sin\alpha+v_0\,,\] \[v_0\,=\,t_\mathrm{z_2}\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right),\] \[t_\mathrm{z_2}\,=\,\frac{v_0}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha}.\tag{31}\]Čas tz2 dosadíme do vztahu (30) a spočteme ujetou vzdálenost sz2:
\[s_\mathrm{z_2}\,=\,-\frac{F_\mathrm{t_2}}{2m}{t_\mathrm{z_2}}^2+ \frac{g{t_\mathrm{z_2}}^2}{2}\sin\alpha+v_0 t_\mathrm{z_2}\,,\] \[s_\mathrm{z_2}\,=\,-\frac{F_\mathrm{t_2}}{2m}\left(\frac{v_0}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha}\right)^2 +\frac{g\left(\frac{v_0}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha}\right)^2}{2}\sin\alpha +v_0\frac{v_0}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha},\] \[s_\mathrm{z_2}\,=\,-\frac{\frac{F_\mathrm{t_2}}{m}v_0^2}{2\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right)^2} +\frac{gv_0^2\sin\alpha}{2\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right)^2} +\frac{v_0^2}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha},\] \[s_\mathrm{z_2}\,=\,-\frac{v_0^2\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right)}{2\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right)^2} +\frac{v_0^2}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha},\] \[s_\mathrm{z_2}\,=\,-\frac{v_0^2}{2\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right)} +\frac{v_0^2}{\frac{F_\mathrm{t_2}}{m}-g\sin\alpha} \,=\,\frac{v_0^2}{2\left(\frac{F_\mathrm{t_2}}{m}-g\sin\alpha\right)}.\]Dosadíme za Ft2 ze vztahu (25):
\[s_\mathrm{z_2}\,=\,\frac{v_0^2} {2\left(\frac{\frac{v_0^2m\cos\alpha}{2s_z}}{m}-g\sin\alpha\right)} \,=\,\frac{v_0^2}{2\left(\frac{v_0^2\cos\alpha}{2s_z}-g\sin\alpha\right)}\,,\] \[s_\mathrm{z_2}\,=\,\frac{s_\mathrm{z}v_0^2}{v_0^2\cos\alpha-2s_\mathrm{z}g\sin\alpha}.\tag{32}\]Do vztahu (32) dosadíme číselně:
\[s_\mathrm{z_2}\,=\,\frac{50\left(\frac{80}{3{,}6}\right)^2}{\left(\frac{80}{3{,}6}\right)^2 \cos 5^{\circ}\,-\,2\,\cdot50\cdot\,9{,}81\sin5^{\circ}}\,\mathrm{m},\] \[s_\mathrm{z_2}\,=\,\frac{50\,\cdot22{,}22^2}{22{,}22^2\,\cdot0{,}997\, -\,981\cdot \,0{,}087}\,\mathrm{m},\] \[s_\mathrm{z_2}\,=\,\frac{50{\cdot}493{,}72}{493{,}72{\cdot}0{,}997-85{,}35}\,\mathrm{m}\,=\, \frac{24\,612}{492{,}24\,-\,85{,}35}\,\mathrm{m}, \] \[s_\mathrm{z_2}\,=\,\frac{24\,612}{406{,}89}\,\mathrm{m}\,=\,60{,}49\,\mathrm{m}\,\dot=\,60{,}5\,\mathrm{m}.\]CELKOVÁ ODPOVĚĎ
Brzdná dráha pro auto jedoucí do kopce na stejné vozovce, která svírá s vodorovnou rovinou úhel α, je \[s_\mathrm{z_1}\,=\,\frac{s_\mathrm{z}v_0^2}{v_0^2\cos\alpha+2s_\mathrm{z}g\sin\alpha}\,\dot=\,42{,}6\,\textrm{m}.\]
Brzdná dráha pro auto jedoucí z kopce na stejné vozovce, která svírá s vodorovnou rovinou úhel α, je \[s_\mathrm{z_2}\,=\, \frac{s_\mathrm{z}v_0^2}{v_0^2\cos\alpha-2s_\mathrm{z}g\sin\alpha}\,\dot=\,60{,}5\,\textrm{m}.\]



