Nit navinutá na kladce
Úloha číslo: 532
Na obvodu kladky o hmotnosti 5 kg a průměru 30 cm jsou navinuty 4 závity režné nitě. Máme za 1 s nit odvinout. Jakou minimální konstantní silou musíme táhnout za nit?
Zápis:
m = 5 kg hmotnost kladky r = 15 cm poloměr kladky n = 4 počet navinutí nitě t = 1 s čas odvinutí F = ? (N) minimální síla, kterou musíme táhnout za nit Moment setrvačnosti:
Kladku můžeme považovat za válec o hmotnosti m a poloměru r. V tabulkách lze nalézt vztah pro moment setrvačnosti válce vzhledem ke geometrické ose:
\[J=\frac{1}{2} mr^2 \,.\tag{0}\](Odvození tohoto vztahu bude uvedeno v jedné z budoucích úloh.)
Rozbor
Úlohu lze řešit pomocí 2. věty impulsové (\(\vec{M}=\frac{d\vec{L}}{dt}\)), kterou je třeba napsat pro otáčející se kladku.
Druhou možností je využít zákon zachování energie. Práce, kterou konáme táhnutím za nit, se mění na pohybovou energii kladky.
Nápověda A1: 2. věta impulsová
Nakreslete si obrázek situace, vyznačte síly působící na kladku. Napište druhou větu impulsovou pro kladku.
Nápověda A2: 2. věta impulsová
Co můžete říci o úhlovém zrychlení kladky? Napište, jak se s časem mění úhel, o který se kladka otočí. Uvědomte si, že tento úhel znáte, máte-li zadaný počet odvinutých závitů nitě.
Nápověda B1: Zákon zachování energie
Napište, čemu je rovna práce, kterou vykonáme při tahu za nit. Uvědomte si, na co se spotřebovává.
Nápověda B2: Zákon zachování energie
Uvědomte si, jaký pohyb vykonává konec nitě, a vyjádřete jeho rychlost v okamžiku odmotání všech závitů.
Celkové řešení pomocí impulsové věty
Nakreslíme si obrázek situace a vyznačíme síly působící na kladku. Napíšeme druhou větu impulsovou pro kladku.
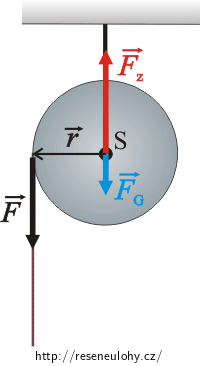
Na kladku působí tíhová síla Fg, závěs silou Fz a nit, za kterou táhneme, silou F.
Druhá impulsová věta říká:
\[\vec{M}=\frac{d\vec{L}}{dt}\,.\]V případě rotace tuhého tělesa kolem pevné osy platí:
\[L = J \omega\,,\] \[\vec{M}=\frac{d\vec{L}}{dt} = J\vec{\epsilon}\,,\]kde \(\vec{M}\) je výsledný moment sil působících na kladku vzhledem ke zvolenému bodu, \(\vec{L}\) je celkový moment hybnosti vzhledem k tomuto bodu, \(J\) moment setrvačnosti kladky vzhledem k pevné ose jdoucí zvoleným bodem a \(\vec{\epsilon}\) úhlové zrychlení kladky.
Pro výsledný moment působících sil vzhledem ke středu kladky S platí:
\[\vec{M}=\vec{r}\times\vec{F} = J\vec{\epsilon}\,.\]Přepíšeme skalárně a dosadíme za moment setrvačnosti:
\[M = rF = \frac{1}{2} mr^2\epsilon\,.\]Vyjádříme úhlové zrychlení kladky:
\[\epsilon =\frac{F}{\frac{1}{2} mr}\,.\tag{1}\]Úhlové zrychlení kladky je konstantní. Úhel, o který se za čas t otočí bod na obvodu kladky, můžeme napsat jako:
\[\alpha = \frac{1}{2}\epsilon t^2\,.\tag{2}\]Zároveň víme, že máme odvinout n závitů nitě. Kladka se tedy otočí o úhel:
\[\alpha = n 2\pi\,.\]Platí tedy (s použitím vztahu (2)):
\[\alpha = n 2\pi = \frac{1}{2}\epsilon t^2\,.\]Dosadíme za úhlové zrychlení ze vztahu (1):
\[n 2\pi = \frac{1}{2}(\frac{F}{\frac{1}{2} mr})t^2\,. \]Upravíme:
\[n 2\pi mr = Ft^2\,.\]Odtud:
\[F = \frac{2n\pi rm}{t^2}\,.\]Číselně:
\[F = \frac{2{\cdot}4\cdot\pi\cdot 0{,}15{\cdot} 5}{1^2}\,\mathrm{N} \dot{=}18{,}9\,\mathrm{N}\,.\]Celkové řešení pomocí zákona zachování energie
Práce konstantní síly působící ve směru pohybu je rovna
\[W=Fs\,,\]kde s je vzdálenost, kterou urazil konec nitě při rozmotávání.
Tato práce je v našem případě spotřebována na roztočení kladky, potažmo změnu její kinetické energie:
\[E=\frac{1}{2}J\omega^2=\frac{1}{2}(\frac{1}{2}mr^2)\omega^2= \frac{1}{4}mr^2(\frac{v}{r})^2=\frac{1}{4}mv^2\,,\]kde \(v\) je obvodová rychlost na konci roztáčení, tj. rychlost, kterou táhneme konec nitě v okamžiku rozmotání všech závitů.
Platí tedy:
\[Fs = \frac{1}{4}mv^2\,.\tag{3}\]Konec nitě koná rovnoměrně zrychlený přímočarý pohyb. Vzdálenost s, kterou urazí, spočítáme z množství nitě namotané na kladce: je to n-krát obvod kladky, kde n je počet závitů:
\[s=2n\pi r.\]K vyjádření hledané rychlosti v použijeme následující vztahy:
\(v=at\) a \(s=\frac{1}{2}at^2,\)
což lze upravit na
\[a=\frac{2s}{t^2}\,.\]Pro rychlost pak dostáváme:
\[v=at=\frac{2s}{t^2}t=\frac{2s}{t}\,.\]Dosadíme postupně do (3):
\[Fs=\frac{1}{4}m(\frac{2s}{t})^2\,,\] \[F=m\frac{s}{t^2}\,,\] \[F=\frac{2n\pi rm}{t^2}\,.\]Číselně:
\[F = \frac{2{\cdot}4\cdot\pi\cdot 0{,}15{\cdot} 5}{1^2}\,\mathrm{N} \dot{=}18{,}9\,\mathrm{N}\,.\]Odpověď
Musíme táhnout silou F:
\[F=\frac{2nm\pi r}{t^2}\,,\] \[F\dot{=}18{,}85\,\mathrm{N}\,.\]



