Dva kvádry na nakloněné rovině
Úloha číslo: 138
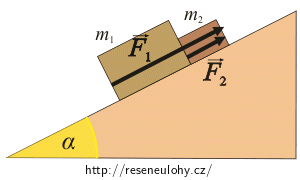
Na nakloněné rovině svírající s vodorovnou rovinou úhel α jsou dva kvádry o hmotnostech m1 a m2. Příslušné koeficienty smykového tření jsou f1 a f2. Na spodní kvádr působíme silou F1, jejíž směr je rovnoběžný s nakloněnou rovinou. Tento spodní kvádr před sebou vytlačuje kontaktní silou F2 druhý kvádr. Určete velikost síly F2.
Zápis
m1 hmotnost prvního (spodního) kvádru m2 hmotnost druhého (vrchního) kvádru f1 koeficient tření mezi prvním kvádrem a rovinou f2 koeficient tření mezi druhým kvádrem a rovinou α sklon roviny F1 velikost síly, kterou působíme na spodní kvádr F2 = ? velikost kontaktní síly, kterou spodní kvádr vytlačuje vrchní Nápověda 1 – síly působící na kvádry
Nakreslete si obrázek a v něm vyznačte, jaké síly působí na jednotlivé kvádry.
Nápověda 2 – pohybové rovnice
Napište pohybové rovnice pro jednotlivé kvádry, zvolte souřadný systém a přepište pohybové rovnice skalárně.
Nápověda 3 – třecí síly
Uvědomte si, na čem závisí velikost třecí síly a jak ji můžete vyjádřit.
Nápověda 4 – výpočet síly
Získali jste dvě rovnice o neznámých F2 a a, které je třeba vyřešit.
CELKOVÉ ŘEŠENÍ
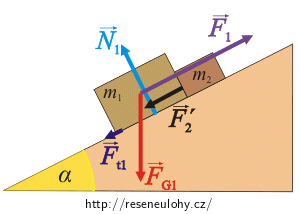
Nejprve nakreslíme do obrázku všechny síly působící na kvádry a napíšeme pro ně pohybové rovnice.
Síly působící na kvádr m1:
\(\vec{F}_\mathrm{G_1}\)…síla tíhová působící na kvádr m1,
\(\vec{F}_1\)…síla, kterou tlačíme na kvádr,
\(\vec{N}_{1}\)…síla, kterou tlačí na kvádr podložka,
\(\vec{F}_\mathrm{t_1}\)…síla třecí působící na kvádr m1,
\(\vec{F}_2\prime\)…síla, kterou tlačí kvádr m2 na kvádr m1.
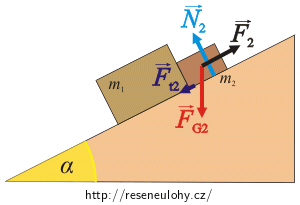
Síly působící na kvádr m2:
\(\vec{F}_\mathrm{G_2}\)…síla tíhová působící na kvádr m2,
\(\vec{F}_2\)…síla, kterou tlačí kvádr m1 na kvádr m2,
\(\vec{N}_{2}\)…síla, kterou tlačí na kvádr podložka,
\(\vec{F}_\mathrm{t_2}\)…síla třecí působící na kvádr m2.
Pohybové rovnice:
\[m_1:\qquad \vec{F}_1+\vec{N_1}+\vec{F}_\mathrm{G_1}+\vec{F}_\mathrm{t_1}+\vec{F}_{2}\prime=m_1\vec{a},\] \[m_2:\qquad \vec{F}_2+\vec{N_2}+\vec{F}_\mathrm{G_2}+\vec{F}_\mathrm{t_2}=m_2\vec{a}.\]Oba kvádry vyjíždějí se stejným zrychlením.
Abychom mohli pohybové rovnice přepsat skalárně, zvolíme si souřadný systém os x, y tak, že osu x zvolíme ve směru pohybu kvádrů. Osa y je kolmá na osu x. Síly FG1 a FG2 rozložíme na 2 složky do směru těchto os:
\[F_\mathrm{G_{1x}}=F_\mathrm{G_1}\sin\alpha,\] \[F_\mathrm{G_{1y}}=F_\mathrm{G_1}\cos\alpha.\]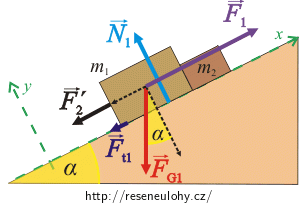
\[F_\mathrm{G_{2x}}=F_\mathrm{G_2}\sin\alpha,\] \[F_\mathrm{G_{2y}}=F_\mathrm{G_2}\cos\alpha.\]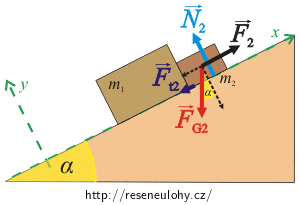
Pohybové rovnice přepíšeme skalárně:
Kvádr m1:
\[ x:\qquad F_1-F_\mathrm{G_1}\sin\alpha-F_\mathrm{t_1}-F_2\prime=m_1a,\tag{1}\] \[y:\qquad N_1-F_\mathrm{G_1}\cos\alpha=0.\tag{2}\]Kvádr m2:
\[x:\qquad F_2-F_\mathrm{G_2}\sin\alpha-F_\mathrm{t_2}=m_2a,\tag{3}\] \[y:\qquad N_2-F_\mathrm{G_2}\cos\alpha=0.\tag{4}\]Třecí síly:
Třecí síla působící na každý kvádr je úměrná tlakové síle, kterou kvádr působí na nakloněnou rovinu. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí nakloněná rovina na kvádr. Zapíšeme to rovnicí:
\[F_\mathrm{t_1}=f_1N_1,\] \[F_\mathrm{t_2}=f_2N_2.\]Síly N1 a N2 vyjádříme z rovnic (2) a (4):
\[N_1=F_\mathrm{G_1}\cos\alpha, \] \[N_2=F_\mathrm{G_2}\cos\alpha. \]Pro třecí síly platí:
\[F_\mathrm{t_1}=f_1F_\mathrm{G_1}\cos\alpha,\] \[F_\mathrm{t_2}=f_2F_\mathrm{G_2}\cos\alpha.\]Kvádr m1 působí silou \(\vec{F}_2\) na kvádr m2 a kvádr m2 zase naopak na kvádr m1 silou \(\vec{F}_2\prime\). Podle 3. Newtonova zákona platí pro velikosti sil:
\[|\vec{F}_2| = |\vec{F}_2\prime|.\]Dosadíme do rovnic (1) a (3) za třecí síly:
\[F_1-F_\mathrm{G_1}\sin\alpha-f_1F_\mathrm{G_1}\cos\alpha - F_2=m_1a,\tag{5}\] \[F_2-F_\mathrm{G_2}\sin\alpha-f_2F_\mathrm{G_2}\cos\alpha=m_2a.\tag{6}\]Výpočet síly F2:
Získali jsme 2 rovnice o neznámých F2 a a, které je třeba vyřešit.
Z rovnice (6) vyjádříme zrychlení:
\[a\,=\,\frac{F_2-F_\mathrm{G_2}\sin\alpha-f_2F_\mathrm{G_2}\cos\alpha}{m_2}.\tag{7}\]Zrychlení z rovnice (7) dosadíme do rovnice (5), rozepíšeme tíhové síly FG1 = m1g, FG2 = m2g a vyjádříme sílu F2:
\[F_1-m_1g\sin\alpha-f_1m_1g\cos\alpha - F_2=m_1\frac{F_2-m_2g\sin\alpha-f_2m_2g\cos\alpha}{m_2}.\]
Rovnici vynásobíme členem m2:
\[m_2F_1-m_2m_1g\sin\alpha-f_1m_2m_1g\cos\alpha-m_2F_2=\] \[m_1F_2-m_2m_1g\sin\alpha-f_2m_2m_1g\cos\alpha.\]Na jedné straně rovnice necháme členy s neznámou F2, na druhé straně členy zbývající:
\[m_2F_1-m_2m_1g\sin\alpha-f_1m_2m_1g\cos\alpha+m_2m_1g\sin\alpha+\] \[+f_2m_2m_1g\cos\alpha =m_1F_2+m_2F_2.\]Po úpravě dostáváme:
\[m_2F_1-f_1m_2m_1g\cos\alpha+f_2m_2m_1g\cos\alpha =\left(m_1+m_2\right)F_2.\]Vyjádříme neznámou F2:
\[F_2\,=\,\frac{m_2F_1+m_2m_1f_2g\cos\alpha-m_2m_1f_1g\cos\alpha}{m_1+m_2},\] \[F_2\,=\,\frac{m_2F_1+m_2m_1g\cos\alpha\left(f_2-f_1\right)}{m_1+m_2},\] \[F_2\,=\,\frac{m_2\left[F_1+m_1g\cos\alpha\left(f_2-f_1\right)\right]}{m_1+m_2}.\]CELKOVÁ ODPOVĚĎ
Velikost síly F2 působící na kvádr m2 je \[F_2\,=\,\frac{m_2\left[F_1+m_1g\cos\alpha\left(f_2-f_1\right)\right]}{m_1+m_2}.\]
