Nakloněná rovina - tři tělesa
Úloha číslo: 96
Vyobrazená soustava klouže dolů po nakloněné rovině. Určete velikost zrychlení soustavy a velikosti tahových sil provázků T1, T2. Koeficient smykového tření mezi bloky a nakloněnou rovinou je f. Moment setrvačnosti kladky a hmotnost provázku zanedbejte.
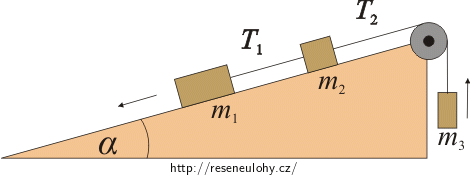
Zápis
m1 hmotnost prvního závaží m2 hmotnost druhého závaží m3 hmotnost třetího závaží f koeficient tření mezi závažími a rovinou α sklon roviny T1 = ? velikost tahové síly provázku mezi závažími m1 a m2 T2 = ? velikost tahové síly provázku mezi závažími m2 a m3 a = ? velikost zrychlení soustavy Nápověda 1 – pohybové rovnice
Nakreslete si obrázek, vyznačte v něm, jaké síly působí na jednotlivá závaží, a napište pro jednotlivá závaží pohybové rovnice.
Nápověda 2 – třecí síly
Uvědomte si, na čem závisí velikost třecích sil, a jak ji můžeme vyjádřit.
Nápověda 3 - velikost zrychlení a provázkových sil
Dostáváte 3 rovnice (8), (9), (10) o třech neznámých. Po jejich vyřešení dostanete velikost zrychlení a obou provázkových sil.
CELKOVÉ ŘEŠENÍ
Do obrázku nakreslíme všechny síly působící na jednotlivá závaží a napíšeme pro ně pohybové rovnice.
Síly působící na závaží:
Na první závaží m1 působí tyto síly:
\(\vec{F}_\mathrm{G1}\)…síla tíhová
\(\vec{N}_{1}\)…síla, kterou tlačí podložka
\(\vec{T}_{1}\)…tahová síla provázku
\(\vec{F}_\mathrm{t1}\)…síla třecí
Na druhé závaží m2 působí tyto síly:
\(\vec{F}_\mathrm{G2}\)…síla tíhová
\(\vec{N}_{2}\)…síla, kterou tlačí podložka
\(\vec{T}_{2}\)…tahová síla provázku
\(\vec{T}_{1}\prime\)…tahová síla provázku
\(\vec{F}_\mathrm{t2}\)…síla třecí
Na třetí závaží m3 působí tyto síly:
\(\vec{F}_\mathrm{G2}\)…síla tíhová
\(\vec{T}_{2}\prime\)…tahová síla provázku
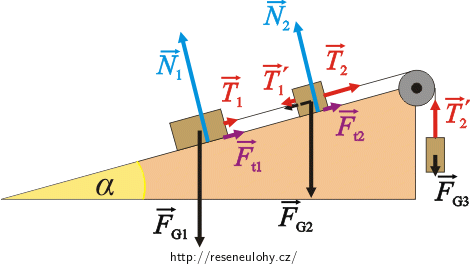
Pohybové rovnice pro jednotlivá závaží:
Všechna 3 závaží jsou propojena provázky, pohybují se se stejným zrychlením.
\[m_1:\qquad \vec{F}_\mathrm{G1} + \vec{N}_1 + \vec{F}_\mathrm{t1} + \vec{T}_1\,=\,m_1\vec{a},\]
\[m_2:\qquad \vec{F}_\mathrm{G2} + \vec{N}_2 + \vec{F}_\mathrm{t2} + \vec{T}_1\prime + \vec{T}_2\,=\,m_2\vec{a},\] \[m_3:\qquad \vec{F}_\mathrm{G3} + \vec{T}_2\prime\,=\,m_3\vec{a}.\]Abychom mohli pohybové rovnice přepsat skalárně, zvolíme si souřadný systém os x, y tak, že osu x zvolíme ve směru pohybu závaží. Osa y je kolmá na osu x.

Síly \(\vec{F}_\mathrm{G_1}\) a \(\vec{F}_\mathrm{G_2}\) rozložíme na 2 složky do směru těchto os:
\[F_\mathrm{{G1}_x}\,=\,F_\mathrm{G1}\sin\alpha,\] \[F_\mathrm{{G1}_y}\,=\,F_\mathrm{G1}\cos\alpha,\] \[F_\mathrm{{G2}_x}\,=\,F_\mathrm{G2}\sin\alpha,\] \[F_\mathrm{{G2}_y}\,=\,F_\mathrm{G2}\cos\alpha.\]Pohybové rovnice přepíšeme skalárně:
\[m_\mathrm{x1}:\qquad F_\mathrm{G1}sin\alpha - F_\mathrm{t1} - T_1\,=\,m_1a,\tag{1}\] \[m_\mathrm{x2}:\qquad F_\mathrm{G2}sin\alpha - F_\mathrm{t2} + T_1\prime - T_2\,=\,m_2a,\tag{2}\] \[m_\mathrm{x3}:\qquad -F_\mathrm{G3} + T_2\prime\,=\,m_3a,\tag{3}\] \[m_\mathrm{y_1}:\qquad N_1 - F_\mathrm{G1} cos\alpha \,=\, 0,\tag{4}\] \[m_\mathrm{y_2}:\qquad N_2 - F_\mathrm{G2} cos\alpha \,=\, 0.\tag{5}\]Ve směru osy y se závaží nepohybují, proto je zrychlení rovno nule.
Jelikož hmotnost kladky zanedbáváme, nemá žádný moment setrvačnosti a neovlivňuje provázkové síly. Závaží m3 působí prostřednictvím provázku na závaží m2 a závaží m2 zase naopak na závaží m3. Obdobně je tomu se závažími m1 a m2. Podle 3. Newtonova zákona platí pro velikosti sil:
\[|\vec{T}_1| \,=\, |\vec{T}_1\prime|,\] \[|\vec{T}_2| \,=\, |\vec{T}_2\prime|.\]Třecí síly:
Třecí síla působící na závaží je úměrná tlakové síle, kterou závaží působí na nakloněnou rovinu. Ta je podle 3. Newtonova zákona stejně velká jako síla, kterou tlačí nakloněná rovina na závaží. Zapíšeme to rovnicí:
\[F_\mathrm{t1}\,\,=\,\,fN_1,\] \[F_\mathrm{t2}\,=\,fN_2.\]Síly N1 a N2 vyjádříme z rovnic (4) a (5):
\[N_1\,=\,F_\mathrm{G1}\cos\alpha, \] \[N_2\,=\,F_\mathrm{G2}\cos\alpha. \]Pro třecí síly platí:
\[F_\mathrm{t1}\,=\,fF_\mathrm{G1}\cos\alpha,\] \[F_\mathrm{t2}\,=\,fF_\mathrm{G2}\cos\alpha.\]Dosadíme do pohybových rovnic (1) a (2):
\[m_\mathrm{x_1}:\qquad F_\mathrm{G1}\sin\alpha-fF_\mathrm{G1}\cos\alpha-T_1\,=\,m_1a,\tag{6}\] \[m_\mathrm{x_2}:\qquad F_\mathrm{G2}\sin\alpha-fF_\mathrm{G2}\cos\alpha+T_1-T_2\,=\,m_2a.\tag{7}\]Dosadíme za \(F_\mathrm{{G1}}\,=\,m_1g\), \(F_\mathrm{{G2}}\,=\,m_2g\) a \(F_\mathrm{G_3}\,=\,m_3g\) a přepíšeme rovnice (6), (7) a (3):
\[m_\mathrm{x_1}:\qquad m_1g\sin\alpha - m_1gf \cos\alpha-T_1\,=\,m_1a,\tag{8}\] \[m_\mathrm{x_2}:\qquad m_2g\sin\alpha - m_2gf \cos\alpha + T_1 - T_2\,=\,m_2a,\tag{9}\] \[m_\mathrm{x_3}:\qquad -m_3g + T_2\,=\,m_3a.\tag{10}\]Nejprve spočteme velikost zrychlení a:
Sečtením rovnic (8), (9) a (10) dostáváme:
\[m_1g\sin\alpha-m_1gf\cos\alpha+m_2g\sin\alpha-m_2gf\cos\alpha-m_3g\,=\,\]
\[\,=\,m_2a+m_3a+m_1a,\] \[a\,=\,\frac{m_1g\sin\alpha-m_1gf\cos\alpha+ m_2g\sin\alpha-m_2gf\cos\alpha-m_3g}{m_2+m_3+m_1},\] \[a\,=\,\frac{g\left[m_1(\sin\alpha-f\cos\alpha)+ m_2(\sin\alpha-f\cos\alpha)-m_3\right]}{m_2+m_3+m_1},\] \[a\,=\,\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}.\tag{11}\]Nyní spočteme velikost provázkové síly T1:
Dosadíme zrychlení ze vztahu (11) do rovnice (8):
\[m_1g\sin\alpha - m_1gf \cos\alpha-T_1\,=\,\] \[\,=\,m_1\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}.\]Vyjádříme T1 a upravíme:
\[T_1\,=\,m_1g\sin\alpha-m_1gf \cos\alpha-m_1\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1},\]
\[T_1\,=\,m_1g(\sin\alpha-f\cos\alpha)-\frac{m_1g(m_1+m_2)(\sin\alpha-f\cos\alpha)-m_1m_3g}{m_2+m_3+m_1}.\]
Převedeme na společného jmenovatele a upravíme:
\[T_1\,=\,\frac{m_1g(\sin\alpha-f\cos\alpha)\left[(m_2+m_3+m_1) -(m_2+m_1)\right]+m_3m_1g}{m_2+m_3+m_1},\] \[T_1\,=\,\frac{m_3m_1g\left(\sin\alpha-f\cos\alpha \right)+m_3m_1g}{m_2+m_3+m_1},\] \[T_1\,=\,\frac{m_1m_3g(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}.\tag{12}\]Nyní spočteme velikost provázkové síly T2:
T2 spočteme z rovnice (10):
\[T_2\,=\,m_3(a+g).\]Dosadíme zrychlení ze vztahu (11):
\[T_2\,=\,m_3\left[\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g} {m_2+m_3+m_1}+g \right].\]Převedeme na společného jmenovatele a upravíme:
\[T_2\,=\,m_3\left[\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g+(m_2+m_1)g+m_3g} {m_2+m_3+m_1}\right],\] \[T_2\,=\,\frac{m_3g(m_2+m_1)(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}.\tag{13}\]CELKOVÁ ODPOVĚĎ
Velikost zrychlení soustavy je
\[a\,=\,\frac{(m_1+m_2)g(\sin\alpha-f\cos\alpha)-m_3g}{m_2+m_3+m_1}\,.\]Velikost tahové síly provázku mezi závažími m1 a m2 je
\[T_1\,=\,\frac{m_1m_3g(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}\,.\]Velikost tahové síly provázku mezi závažími m2 a m3 je
\[T_2\,=\,\frac{m_3g(m_2+m_1)(1+\sin\alpha-f\cos\alpha)}{m_2+m_3+m_1}\,.\]






