Nůžky a zavěšená tyč
Úloha číslo: 1252
Tyč o délce \(3l\), jejíž hmotnost zanedbáváme, je zavěšena ve vodorovné poloze pomocí dvou vláken, upevněných na koncích tyče. Na tyči jsou nasazeny koule o hmotnostech \(m\) a \(2m\) tak, že jejich středy leží v jedné, resp. dvou třetinách délky tyče. Poloměry koulí jsou malé oproti délce tyče.
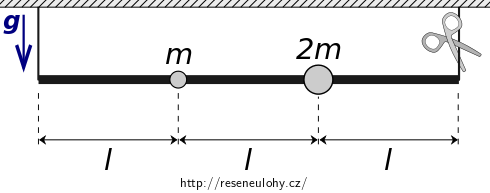
Spočítejte, jak se změní síla napínající vlákno na straně menší koule v okamžiku, kdy druhé vlákno přestřihneme?
Průpravná rukojeť
Při řešení úloh lze v některých případech tuhé těleso s výhodou nahradit soustavou hmotných bodů. V této úloze toho budeme využívat.První věta impulsová
Výslednice všech vnějších sil působících na soustavu hmotných bodů je rovna časové změně celkové hybnosti soustavy. Současně platí druhá rovnost, jakési zobecnění Newtonova zákona síly na soustavu hmotných bodů, kde \(\vec{a_\mathrm{T}}\) je zrychlení těžistě soustavy a \(m\) hmotnost soustavy:
\[\sum_{i=1}^{N}\vec{F}_i = \frac{\mathrm{d}\vec{p}}{\mathrm{d}t}= m\vec{a}_\mathrm{T}. \] Je-li zrychlení těžiště soustavy nulové (je v klidu nebo se pohybuje rovnoměrně přímočaře), z první věty impulsové plyne \[\sum_{i=1}^{N}\vec{F}_i = \vec{0}.\]Druhá věta impulsová
Druhá věta impulsová říká, že výslednice všech momentů vnějších sil na soustavu působících je rovna časové změně celkového momentu hybnosti soustavy. V případě rotace kolem pevné osy platí druhá rovnost, kde \(J\) je moment setrvačnosti vůči dané ose a \(\vec{\varepsilon}\) úhlové zrychlení. \[\sum_{i=1}^{N}\vec{M}_i = \frac{\mathrm{d}\vec{L}}{\mathrm{d}t}= J\vec{\varepsilon}. \]Vztah úhlových a obvodových veličin
Bod \(\mathrm{T}\) vykonává otáčivý pohyb kolem bodu \(\mathrm{O}\) tak, že \(|\mathrm{OT}| = \mathrm{konst.}\)
Jeho polohy v časech \(t\) a \(t + \mathrm{d}t\) jsou zakresleny v následujícím obrázku.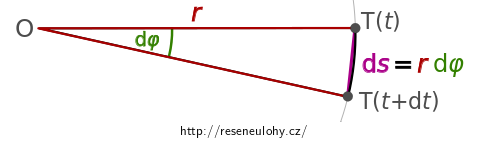
Elementární posunutí \(\mathrm{d}s\) na oblouku kružnice o poloměru \(r = |\mathrm{OT}|\) při otočení o elementární úhel \(\mathrm{d}\varphi\) (v radiánech!) je
\[\mathrm{d}s = r \mathrm{d} \varphi.\] Zajímá-li nás velikost zrychlení takového pohybu, které je druhou derivací dráhy podle času, lze užitím předešlého vztahu postupnými úpravami získat \[a = \frac{\mathrm{d}^2 s}{\mathrm{d}t^2} = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\mathrm{d}s}{\mathrm{d}t}\right) = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{r\mathrm{d}\varphi}{\mathrm{d}t}\right) = r\frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\mathrm{d}\varphi}{\mathrm{d}t}\right) = r \frac{\mathrm{d}^2 \varphi}{\mathrm{d}t^2} = r\varepsilon,\] tj. souvislost mezi obvodovým zrychlením na levé a úhlovým zrychlením na pravé straně.Poznámka: Všimněte si, že v průběhu úprav je poloměr \(r\) vytknut před derivaci. Tato úprava je možná, právě a jen tehdy, je-li \(r\) konstantní. V této úloze je poloha těžiště vůči ose otáčení konstantní, takže tento vztah bude možno použití.
Výpočet polohy těžiště
Jsou-li hmotné body \(m_i\) na přímce a \(x_i\) jejich souřadnice vůči bodu \(\mathrm{O}\), je souřadnice těžiště dána vztahem \[x_\mathrm{T} = \frac{\sum_{i=1}^N m_i x_i}{\sum_{i=1}^N m_i}.\]Moment setrvačnosti
Moment setrvačnosti je aditivní veličina. Máme-li soustavu hmotných bodů \(m_i\), jejichž vzdálenost od osy otáčení je \(\vec{r}_i\), je výsledný moment setrvačnosti vůči této ose \[J = \sum_{i=1}^N m_i r_i^2.\]Zápis
\(m, 2m\) hmotnosti koulí \(l\) vzdálenost sousedních koulí
\(\tilde T_1^\prime/ \tilde T_1 = \mathrm{?}\) poměr síly napínající vlákno po a před přestřihnutím vlákna Nápověda 1 – síla před přestřihnutím
Do obrázku zakreslete všechny síly, které na tyč s koulemi působí. Tyč s koulemi je před přestřihnutím v klidu – výslednice vektorů působících vnějších sil a jejich momentů je nutně rovna nule.
Zapište rovnice vyjadřující podmínky rovnováhy a vyjádřete sílu, kterou na tyč s koulemi působí levé vlákno.Nápověda 2 – síla po přestřihnutí
Po přestřihnutí pravého vlákna se začne soustava tvořená tyčí a koulemi otáčet kolem bodu \(\mathrm{O}\).
Zakreslete všechny vnější síly, které na soustavu působí. Pak rozepište pro soustavu impulsové věty, tj. vyjádřete pravé strany rovnic
\[M\vec{a_\mathrm{T}} = \sum_{i=1}^N \vec{F_i}, \qquad J\vec{\varepsilon} = \sum_{i=1}^N \vec{M_i}\]a přepište je do skalární podoby.
Nápověda 3 – síla po přestřihnutí
- Určete, jaký je moment setrvačnosti \(J\) soustavy vůči ose otáčení, považujeme-li koule vzhledem k malým poloměrům za hmotné body.
- Uvědomte si, jak závisí zrychlení těžiště \(a_\mathrm{t}\) na úhlovém zrychlení \(\varepsilon\).
- Vyjádřete souřadnici těžiště soustavy vůči bodu O.
Nalezněte velikost síly \(T_1^\prime\), kterou na tyč působí levé vlákno těsně po přestřihnutí vlákna pravého.
Nápověda 4 – změna síly v okamžiku přestřižení
Máme vyjádřené síly \(T_1\), \(T_1'\), které působí před a po přestřižení vlákna na tyč.
Jaké jsou ve stejných okamžicích síly \(\tilde T_1\), \(\tilde T_1'\) napínající vlákno? Jak se změní síla napínající levé vlákno při přestřižení pravého vlákna?
CELKOVÉ ŘEŠENÍ
Do obrázku zakreslíme všechny vnější síly, které na tyč s koulemi před přestřižením vlákna působí:- tíhové síly \(\vec{F_{\mathrm{G1}}}\), \(\vec{F_{\mathrm{G2}}}\) působící na koule o hmotnostech \(m\) a \(2m\),
- tahové síly \(\vec{T_1}\) a \(\vec{T_2}\), kterými na konce tyče působí vlákna.
- Tíhová síla působící na tyč je nulová, neboť její hmotnost zanedbáváme.
Tyč s koulemi je v klidu, výslednice vnějších sil i jejich momentů je nutně nulová, tj. \[ \vec{F_{\mathrm{G1}}} + \vec{F_{\mathrm{G2}}} + \vec{T_1} + \vec{T_2} = \vec{0}, \] \[ \vec{l}\times\vec{F_{\mathrm{G1}}} + 2\vec{l}\times\vec{F_{\mathrm{G2}}} + \vec{0} \times \vec{T_1} + 3\vec{l}\times\vec{T_2} = \vec{0}, \] kde momenty jsou vztaženy k levému konci tyče, tj. bodu \(\mathrm{O}\).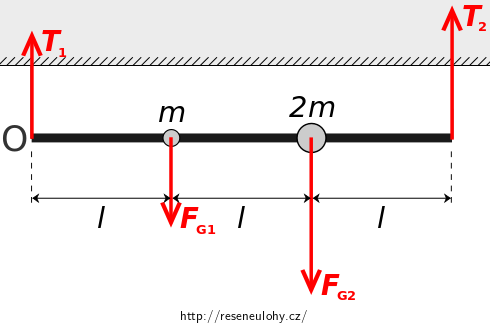
Rovnice přepíšeme do skalární podoby
\[ {F_{\mathrm{G1}}} + {F_{\mathrm{G2}}} - {T_1} - {T_2} = 0, \] \[ -{lF_{\mathrm{G1}}} - 2l{F_{\mathrm{G2}}} + 3l{T_2} = 0, \] kde velikosti momentů směřující před nákresnu jsou kladné, za nákresnu záporné.Dosazením za velikosti tíhových sil získáme rovnice
\[ mg + 2mg - {T_1} - {T_2} = 0, \tag{1}\] \[ -lmg - 4lmg + 3l{T_2} = 0. \tag{2}\]Druhou rovnici vydělíme l a upravíme:
\[3{T_2} = 5mg,\] \[T_2 = \frac{5}{3}mg.\]Z rovnice (1) vyjádříme hledané \(T_1\), do ní pak dosadíme za \(T_2\):
\[T_1 = 3mg - T_2,\] \[ T_1 = 3mg - \frac{5mg}{3} = \frac{4}{3}mg. \tag{A}\]
Do obrázku nyní zakreslíme všechny vnější síly, které na tyč s koulemi působí po přestřižení pravého vlákna:- tíhové síly \(\vec{F_{\mathrm{G1}}}\), \(\vec{F_{\mathrm{G2}}}\) působící na koule se nezmění,
- tahová síla \(\vec{T_2}\) s přestřihnutím vlákna přestane působit,
- tahová síla \(\vec{T_1}\) se změní na sílu \(\vec{T_1^\prime}\).
- Tíhová síla působící na tyč je opět nulová, neboť její hmotnost zanedbáváme.
Tyč se začne otáčet kolem bodu \(\mathrm{O}\).
Dle vět impulsových sestavíme pohybové rovnice: \[ \vec{F_{\mathrm{G1}}} + \vec{F_{\mathrm{G2}}} + \vec{T_1^\prime} = M\vec{a_\mathrm{T}}, \] \[ \vec{l}\times\vec{F_{\mathrm{G1}}} + 2\vec{l}\times\vec{F_{\mathrm{G2}}} + \vec{0} \times \vec{T_1^\prime} = J\vec{\varepsilon}, \] kde \(M\) je hmotnost soustavy, \(J\) moment setrvačnosti vůči ose otáčení a \(\varepsilon\) úhlové zrychlení. Momenty jsou opět vztaženy k levému konci tyče, tj. bodu \(\mathrm{O}\).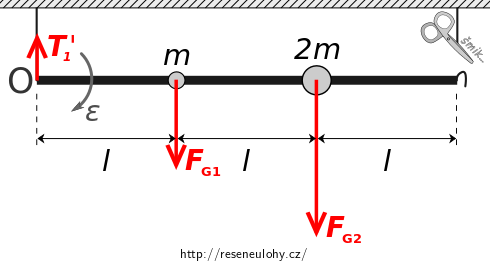
Rovnice přepíšeme do skalární podoby:
\[ {F_{\mathrm{G1}}} + {F_{\mathrm{G2}}} - {T_1^\prime} = Ma_\mathrm{T}, \] \[ -{lF_{\mathrm{G1}}} - 2l{F_{\mathrm{G2}}} = -J\varepsilon, \] kde velikosti momentů směřující před nákresnu jsou kladné, za nákresnu záporné.Dosazením za velikosti tíhových sil a hmotnosti soustavy \(M = 3m\) získáme rovnice:
\[ 3mg - T_1^\prime = 3m a_\mathrm{T}, \tag{3}\] \[ 5lmg = J\varepsilon. \tag{4}\] Moment setrvačnosti \(J\) soustavy vzhledem k ose procházející bodem \(\mathrm{O}\) s nahrazením koulí hmotnými body je \[ J = ml^2 + 2m(2l)^2 = 9ml^2. \tag{5}\] Koule jsou na tyči pevně přichycené. Těžiště je stejně jako osa otáčení neměnné. Vzdálenost těžiště od osy je tedy konstantní a zrychlení těžiště \(a_\mathrm{T}\) je tímto poloměrem otáčení vázáno vzhledem k úhlovému zrychlení \(\varepsilon\) vztahem \[a_\mathrm{T}=r_\mathrm{T} \varepsilon.\tag{6}\]Poloměr otáčení těziště \(r_\mathrm{T}\) je souřadnice těžiště vůči bodu \(\mathrm{O}\), tj.
\[r_\mathrm{T} = \frac{ml + 2m2l}{m+2m} = \frac{5}{3}l.\tag{7}\]Do rovnice (3) dosadíme za \(a_\mathrm{T}\) z (6), do které jsme za \(r_\mathrm{T}\) dosadili z (7). Do rovnice (4) dosadíme za \(J\) z (5):
\[3mg-T_1^\prime = 3m \frac{5}{3} l \varepsilon,\tag{8}\] \[5lmg = 9ml^2\varepsilon.\tag{9}\] Rovnice (8) a (9) vydělíme, tím vyloučíme \(\varepsilon\) a vyjádříme hledané \(T_1^\prime\): \[ \frac{3mg-T_1^\prime}{5lmg} = \frac{5}{9l} \] \[ \Longrightarrow T_1^\prime = \frac{2}{9}mg. \tag{B}\]
Levé vlákno působí na levý konec tyče silou \(T_1\) (resp. \(T_1^\prime\)), konec tyče na stejné vlákno působí silou \(\tilde T_1\) (resp. \(\tilde T_1^\prime\)), která napíná vlákno. Ze zákona akce a reakce pro velikosti sil platí: \[T_1 = \tilde T_1 \qquad a \qquad T_1 = \tilde T_1^\prime.\] Poměr sil napínajících vlákno je tedy \[\frac{\tilde T_1^\prime}{\tilde T_1} = \frac{T_1^\prime}{T_1} = \frac{\frac{2}{9}mg}{\frac{4}{3}mg} = \frac{1}{6},\] kde jsme užili výsledků (A) a (B).Odpověď
V okamžiku přestřižení se síla napínající vlákno na levém konci tyče zmenší šestkrát.



