Bedna na nakloněné rovině s kladkou
Úloha číslo: 95
Za jakou dobu sjede bedna o hmotnosti m1 délku s po nakloněné rovině s úhlem sklonu α, je-li bedna pomocí provazu a kladky spojena s kbelíkem o hmotnosti m2? Vzájemný poměr m1/m2 je takový, že pohyb probíhá po nakloněné rovině směrem dolů. Tření, moment setrvačnosti kladky a hmotnost provazu zanedbejte.

Zápis
m1 hmotnost bedny m2 hmotnost kbelíku s vzdálenost, kterou bedna ujede α sklon roviny t = ? čas, za který bedna urazí dráhu s Nápověda 1 – pohybové rovnice
Nakreslete si obrázek a vyznačte v něm všechny síly působící na bednu a kbelík. Napište pohybovou rovnici pro bednu a pro kbelík.
Nápověda 2 – zrychlení bedny
Z pohybových rovnic (4) a (5) vyjádřete zrychlení bedny.
Řešení k nápovědě 2 – zrychlení vozíku
Dostáváme soustavu dvou rovnic o dvou neznámých, po jejím vyřešení získáme zrychlení soustavy.
Sečteme-li obě rovnice (4) a (5), dostáváme:
\[m_1g \sin\alpha \,-\, m_2g\,=\,\left(m_1+m_2\right)a\,,\] \[a\,=\,\frac{\left(m_1 \sin\alpha \,-\, m_2\right)g}{m_1\,+\,m_2}.\tag{6}\]Vztah (6) udává velikost zrychlení, se kterým bedna sjíždí po nakloněné rovině.
Nápověda 3 – doba, za kterou bedna urazí dráhu s
Závisí zrychlení bedny na čase? O jaký typ pohybu jde? Jak můžete v tomto případě vyjádřit uraženou dráhu?
CELKOVÉ ŘEŠENÍ
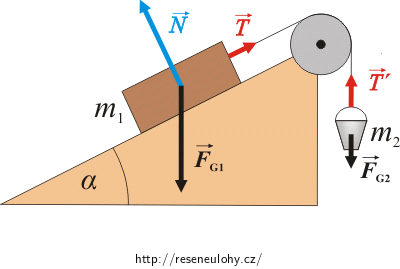
Síly působící na bednu a kbelík:
Na bednu působí tyto síly:
\(\vec{F}_\mathrm{G1}\)…síla tíhová
\(\vec{N}\)…tlaková síla podložky
\(\vec{T}\)…tahová síla provazu
Na kbelík působí tyto síly:
\(\vec{F}_\mathrm{G1}\)…síla tíhová
\(\vec{T^{'}}\)…tahová síla provazu
Pohybové rovnice:
Bedna i kbelík se pohybují se stejným zrychlením.
Pro bednu:
\[\vec{F}_\mathrm{G1}+\vec{N}+\vec{T}\,=\,m_1\vec{a}\]Pro kbelík:
\[\vec{F}_\mathrm{G2}+\vec{T^{'}}\,=\,m_2\vec{a}\]Abychom mohli pohybové rovnice přepsat skalárně, zvolíme si souřadný systém os x, y tak, že osu x zvolíme ve směru pohybu bedny (kbelíku) a osu y kolmo na osu x.
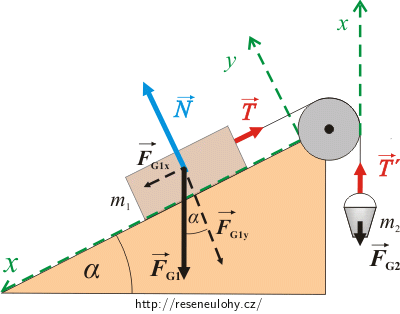
Sílu \(F_\mathrm{G1}\) rozložíme na 2 složky do směru těchto os:
\[F_\mathrm{{G1}_x}\,=\,F_\mathrm{G1}\sin\alpha,\] \[F_\mathrm{{G1}_y}\,=\,F_\mathrm{G1}\cos\alpha.\]Pohybové rovnice přepíšeme skalárně:
Pro bednu:
\[x:\qquad F_\mathrm{G1} sin\alpha - T \,=\, m_1a\tag{1}\] \[y:\qquad N - F_\mathrm{G1} cos\alpha \,=\, 0\tag{2}\]Ve směru osy y se bedna nepohybuje, proto je zrychlení rovno nule.
Pro kbelík:
\[x:\qquad T^{'} - F_\mathrm{G2} \,=\, m_2a\tag{3}\]Jelikož hmotnost kladky zanedbáváme, nemá žádný moment setrvačnosti a neovlivňuje provazové síly. Kbelík působí prostřednictvím provazu na bednu a bedna zase na kbelík. Podle 3. Newtonova zákona platí:
\[\left|\vec{T}\right|\,=\,\left|\vec{T^{'}}\right|\,.\]Dosadíme za \(F_\mathrm{G1}\,=\,m_1g\), \( F_\mathrm{G2}\,=\,m_2g\) a přepíšeme rovnice (1) a (3):
\[m_1g sin\alpha - T \,=\, m_1a,\tag{4}\] \[T - m_2g\,=\, m_2a.\tag{5}\]Dostáváme soustavu dvou rovnic o dvou neznámých, po jejím vyřešení získáme zrychlení soustavy.
Sečteme-li obě rovnice (4) a (5), dostáváme:
\[m_1g \sin\alpha \,-\, m_2g\,=\,\left(m_1+m_2\right)a\,,\] \[a\,=\,\frac{\left(m_1 \sin\alpha \,-\, m_2\right)g}{m_1\,+\,m_2}.\tag{6}\]Vztah (6) udává velikost zrychlení, se kterým bedna sjíždí po nakloněné rovině.
Výpočet času, za který bedna urazí dráhu s:
Ze vztahu (6) vidíme, že zrychlení bedny nezávisí na čase. Jde tedy o pohyb rovnoměrně zrychlený, pro nějž platí vztah pro uraženou dráhu s:
\[s\,=\,\frac{at^2}{2}\,.\tag{7}\]t… čas, za který ujede bedna dráhu s
Ze vztahu (7) vyjádříme čas t:
\[t\,=\, \sqrt{\frac{2s}{a}}\,.\tag{8}\]Do vztahu (8) dosadíme zrychlení ze vztahu (6):
\[t\,=\,\sqrt{\frac{2s\left(m_1\,+\,m_2\right)}{\left(m_1 \sin\alpha \,-\, m_2\right)g}}\,.\tag{9}\]CELKOVÁ ODPOVĚĎ
Bedna sjede délku s po nakloněné rovině za dobu \[t\,=\,\sqrt{\frac{2s\left(m_1\,+\,m_2\right)}{\left(m_1 \sin\alpha \,-\, m_2\right)g}}\,.\]




