Beruška na válci
Úloha číslo: 121
Válec o poloměru R a výšce h se otáčí rovnoměrně kolem vlastní osy ve směru otáčení hodinových ručiček tak, že vykoná jednu otočku za čas T. Po povrchové přímce válce slézá beruška stálou rychlostí v vzhledem k válci.
a) Určete průběh polohového vektoru berušky, byla-li v čase t = 0 s na horním okraji válce.
b) Určete průběh velikosti rychlosti berušky.
c) Určete závislost velikosti tečného a normálového zrychlení berušky na čase.
d) Jaká křivka je trajektorií pohybu? Určete její poloměr křivosti.
e) Jakou dráhu beruška opíše, než doleze až ke spodnímu okraji válce?
Řešte z pohledu pevného pozorovatele stojícího vedle válce.
Soustavu souřadnic volte tak, že osa z je osou válce, osy x a y leží v jeho dolní podstavě.
Nápověda 1 pro a): Obrázek situace
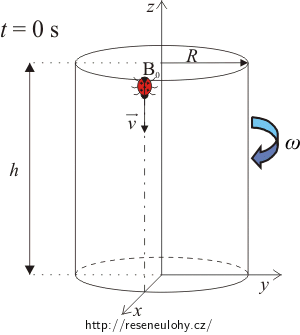
Počátek souřadné soustavy zvolte ve středu spodní podstavy válce a počáteční polohu berušky B0 na obvodě horní podstavy válce.
Nakreslete situaci pro čas t = 0 s a vyznačte polohu berušky B0.
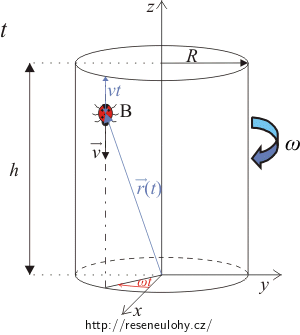
Pak nakreslete situaci pro čas t a vyznačte polohu berušky B, kam za čas t na válci popolezla.
Vyznačte do obrázku i polohový vektor berušky v čase t a jeho průmět do roviny xy.
Nápověda 2 pro a): Průběh polohového vektoru berušky
Pohyb berušky si rozložte na pohyb ve směru osy z a pohyb v rovině xy.
O jaké pohyby se jedná?
Zapište, jak se s časem budou měnit souřadnice x, y, z berušky, a pak s jejich pomocí vyjádřete polohový vektor.
Nápověda 3 pro b): Průběh velikosti rychlosti berušky
Vyjádřete si nejprve složky rychlosti vx, vy, vz. Jakým způsobem je získáte z parametrických rovnic ve směru souřadnicových os?
Pak zapište průběh velikosti rychlosti berušky.
Nápověda 4 pro c): Velikost tečného a normálového zrychlení berušky
Velikost tečného zrychlení snadno zjistíte, znáte-li velikost rychlosti berušky z předchozí nápovědy.
Pro velikost normálového zrychlení budete potřebovat kromě velikosti tečného také velikost celkového zrychlení berušky (to získáte opět ze složek ax, ay, az). Rozmyslete si, jaký mezi nimi platí vztah.
Nápověda 5 pro d): Trajektorie pohybu berušky, poloměr křivosti
Rozmyslete si, jaká křivka by byla trajektorií pohybu berušky, kdyby se válec otáčel a beruška by byla na válci v klidu. Pak k tomu připojte pohyb berušky.
Jaká křivka je trajektorií pohybu?
Pozn.: Uvědomte si, že úlohu řešíte z pohledu pevného pozorovatele stojícího vedle válce.
Jaký je vztah mezi poloměrem křivosti trajektorie, velikostí rychlosti a normálového zrychlení berušky?
Nápověda 6 pro e): Dráha berušky pro případ e)
Dráhu berušky snadno určíte pomocí velikosti rychlosti berušky, kterou znáte, a času, za který doleze odshora na spodní okraj válce. Ten si musíte vyjádřit. Uvědomte si, že znáte výšku válce a rychlost berušky vzhledem k válci.
CELKOVÉ ŘEŠENÍ
Obrázek 1:
Obrázek 2:
a) Pohyb rozložíme na pohyb rovnoměrný přímočarý s rychlostí o velikosti v (ve směru osy z) a pohyb po kružnici s úhlovou rychlostí \(\omega\,=\,\frac{2\pi}{T}\) (v rovině x, y):
\[x\,=\,R\cos\omega{t}\,=\,R\cos\frac{2\pi}{T}t\,,\] \[y\,=\,-R\sin\omega{t}\,=\,-R\sin\frac{2\pi}{T}t\,,\] \[z\,=\,h-vt\,,\] \[\vec{r}\left(t\right)\,=\, R\cos\frac{2\pi}{T}t \vec{\,i\,}-R\sin\frac{2\pi}{T}t\vec{\,j\,}+\left(h-vt\right)\vec{\,k\,}\,,\]kde \(\vec{\,i\,}\), \(\vec{\,j\,}\), \(\vec{\,k\,}\) jsou jednotkové vektory.
b) Složky rychlosti získáme derivací souřadnic podle času:
\[v_\mathrm{x}\,=\,\frac{\mathrm{d}x}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(R\cos\omega t\right)\,=\, -R\omega\sin\omega{t}\,=\,-R\frac{2\pi}{T}\sin\frac{2\pi}{T}t\,, \] \[v_\mathrm{y}\,=\,\frac{\mathrm{d}y}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\sin\omega t\right)\,=\, -R\omega\cos\omega{t}\,=\,-R\frac{2\pi}{T}\cos\frac{2\pi}{T}t\,, \] \[v_\mathrm{z}\,=\,\frac{\mathrm{d}z}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}(h-vt)\,=\, -v\,.\]Průběh velikosti rychlosti berušky je:
\[v_\mathrm{v}\,=\,\left|\vec{v}\left(t\right)\right|\,=\,\sqrt{v_\mathrm{x}^{2}+v_\mathrm{y}^{2}+v_\mathrm{z}^{2}}\,=\, \sqrt{R^{2}\omega^{2}\left(sin^{2}\omega{t}+ cos^{2}\omega{t}\right)+ v^{2}}\,,\] \[v_\mathrm{v}\,=\, \sqrt{v^{2}+R^{2}\omega^{2}} \,=\, \sqrt{v^{2}+R^{2}\left(\frac{2\pi}{T}\right)^{2}}\,=\,\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\,.\]c) Velikost tečného zrychlení at berušky:
\[a_\mathrm{t}\left(t\right)\,=\,\frac{\mathrm{d}v_\mathrm{v}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\sqrt{v^{2}+R^{2}\left(\frac{2\pi}{T}\right)^{2}}\,, \] \[a_\mathrm{t}\,=\,0\,.\]Vztah mezi velikostí tečného at, normálového an a celkového zrychlení a berušky je:
\[a\,=\,\sqrt{a_\mathrm{t}^{2}+ a_\mathrm{n}^{2}}\,,\] \[a_\mathrm{n}\,=\,\sqrt{a^{2}-a_\mathrm{t}^{2}}\,=\,a\,.\]Velikost celkového zrychlení berušky a:
\[a_\mathrm{x}\left(t\right)\,=\, \frac{\mathrm{d}v_\mathrm{x}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\omega\sin\omega t\right)\,=\,-R\omega^{2}\cos\omega{t}\,,\] \[a_\mathrm{x}\left(t\right)\,=\,-R\frac{4\pi^{2}}{T^{2}}\cos\frac{2\pi}{T}t \,,\] \[a_\mathrm{y}\left(t\right)\,=\, \frac{\mathrm{d}v_\mathrm{y}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-R\omega\cos\omega t\right)\,=\,R\omega^{2}\sin\omega{t}\,=\,R\frac{4\pi^{2}}{T^{2}}\sin\frac{2\pi}{T}t\,,\] \[a_\mathrm{z}\left(t\right)\,=\, \frac{\mathrm{d}v_\mathrm{z}}{\mathrm{d}t}\,=\, \frac{\mathrm{d}}{\mathrm{d}t}\left(-v\right)\,=\,0\,,\]
\[a\,=\,\sqrt{a_\mathrm{x}^{2}+a_\mathrm{y}^{2}+a_\mathrm{z}^{2}}\,=\,\sqrt{R^{2}\omega^{4}\cos^{2}\omega{t}+R^{2}\omega^{4}\sin^{2}\omega{t}+0}\,,\] \[a\,=\,R\omega^{2}\,=\,4R\frac{\pi^{2}}{T^{2}}\,.\]Velikost normálového zrychlení an berušky:
\[a_\mathrm{n} \,=\, a\, =\,R\omega^{2}\,=\,4R\frac{\pi^{2}}{T^{2}}\,.\]d) Trajektorie pohybu:
Beruška se pohybuje po šroubovici.
Poloměr křivosti ρ:
\[a_\mathrm{n}\,=\,\frac{v_\mathrm{v}^{2}}{\rho}\,.\]Tedy:
\[\rho\,=\,\frac{v_\mathrm{v}^{2}}{a_\mathrm{n}}\,,\] \[\rho\,=\,\frac{R^{2}\omega^{2}+v^{2}}{R\omega^{2}}\,,\] kde \(\omega\,=\,\frac{2\pi}{T}.\)Tedy:
\[\rho\,=\,\frac{R^{2}\frac{4\pi^{2}}{T^{2}}+v^{2}}{R\frac{4\pi^{2}}{T^{2}}}\,=\,R+\frac{v^{2}T^{2}}{4\pi^{2}R}\,.\]e) Dráha l:
Rychlost berušky vzhledem k okolí je konstantní, takže pro hledanou dráhu l platí:
\[l\,=\,v_\mathrm{v}t\,,\]kde
\[v_\mathrm{v}\, =\, \sqrt{(R^{2}\omega^{2}+v^{2})}\,,\] \[t\,=\,\frac{h}{v}\,,\] \[l\,=\,\left(\frac{h}{v}\right)\sqrt{\left(R^{2}\omega^{2}+v^{2}\right)}\,,\]kde \(\omega\,=\,\frac{2\pi}{T}\,.\)
Tedy:
\[l\,=\,\left(\frac{h}{v}\right)\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\,.\]Odpověď
a) Průběh polohového vektoru berušky je:
\[\vec{r}\left(t\right)\,=\, R\cos\frac{2\pi}{T}t \vec{\,i\,}-R\sin\frac{2\pi}{T}t\vec{\,j\,}+\left(h-vt\right)\vec{\,k\,}\,,\]kde \(\vec{\,i\,}\), \(\vec{\,j\,}\), \(\vec{\,k\,}\) jsou jednotkové vektory ve směru souřadnicových os.
b) Průběh velikosti rychlosti berušky je:
\[v_\mathrm{v}\,=\,\left|\vec{v}\left(t\right)\right|\,=\,\sqrt{v^{2}+R^{2}\omega^{2}}\,=\,\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\,.\]c) Velikost tečného zrychlení at berušky je:
\[a_\mathrm{t}\,=\,\frac{\mathrm{d}v_\mathrm{v}}{\mathrm{d}t}\,=\,0\,.\]Velikost normálového zrychlení an berušky je konstantní a na čase nezávisí:
\[a_\mathrm{n}\,=\,\sqrt{a^{2}-a_\mathrm{t}^{2}}\,=\,R\omega^{2}\,=\,4R\frac{\pi^{2}}{T^{2}}\,.\]d) Trajektorie pohybu:
Beruška se pohybuje po šroubovici.
Poloměr křivosti ρ je:
\[\rho\,=\,\frac{v_\mathrm{v}^{2}}{a_\mathrm{n}}\,,\] \[\rho\,=\,\frac{R^{2}\omega^{2}+v^{2}}{R\omega^{2}}\,=\,R+\frac{v^{2}T^{2}}{4\pi^{2}R}\,.\]e) Dráha l je:
\[l\,=\,\frac{h}{v}\sqrt{R^{2}\omega^{2}+v^{2}}\,=\,\frac{h}{v}\sqrt{4\pi^{2}\frac{R^{2}}{T^{2}}+v^{2}}\,.\]Vizualizace pohybu
Následující aplet slouží k vizualizaci pohybu berušky na válci. Polohu berušky udává polohový vektor \(\vec{r}_{(t)}\), který je znázorněn modře. Vektor rychlosti \(\vec{v}_{(t)}\) je znázorněn červeně a vektor zrychlení \(\vec{a}_{(t)}\) má zelenou barvu. Kliknutím na tlačítko „Zapnout animaci“ se spustí animace pohybu, opětovným kliknutím se animace zastaví. Kliknutím na tlačítko „Zobrazit stopu berušky“ se zapne, nebo vypne stopa bodu B. Obdobně tlačítko „Zobrazit trajektorii berušky“ vykreslí trajektorii bodu B. Tlačítko „Reset“ vrátí aplet do původního stavu.
Z apletu je dobře vidět, že trajektorií této berušky je šroubovice. Také můžeme pozorovat, že vektor zrychlení \(\vec{a}_{(t)}\) je vždy kolmý na vektor rychlosti \(\vec{v}_{(t)}\) a vždy míří kolmo k ose otáčení válce. Z toho můžeme usoudit, že velikost tečného zrychlení \(a_\mathrm{t}\) musí být nulová, pak musí nutně pro vektor normálového zrychlení platit: \(\vec{a}_\mathrm{n}=\vec{a}\). Velikost rychlosti tedy zůstává konstantní, ale směr rychlosti se neustále mění vlivem normálového zrychlení.