Pět částic
Úloha číslo: 1243
Na obrázku k zadání se nachází pět částic o hmotnostech \(m_{1}=m_{2}=m_{3}=m_{4}=3 \mathrm{kg}\), \(M_{5}=9 \mathrm{kg}\), délka \(l=2 \mathrm{cm}\) a úhel \(\alpha=30\mathrm{°}\).
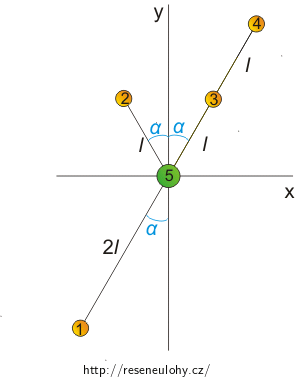
Jakou výslednou gravitační silou \(\vec{F_{5}}\) působí na částici \(5\) ostatní částice?
Zápis
\(m_{1}=m_{2}=m_{3}=m_{4}=3 \mathrm{kg}\) hmotnosti částic \(1{,} 2{,} 3\) a \(4\) \(M_{5}=9 \mathrm{kg}\) hmotnost částice \(5\) \(l=2 \mathrm{cm}\) vzdálenost částice \(5\) a \(2\), vzdálenost částice \(5\) a \(3\), vzdálenost částice \(3\) a \(4\), polovina vzdálenosti částice \(5\) a \(1\) \(\alpha=30\mathrm{°}\) úhel, který svírá přímka procházející částicemi \(1{,} 3{,} 4 \) a \(5\) s osou \(y\), úhel, který svírá přímka procházející částicemi \(2\) a \(5\) s osou \(y\)
Nápověda 1
Do obrázku zakreslete síly, které působí na částici \(5\).
Nápověda 2
Formulujte Newtonův gravitační zákon.
Nápověda 3
S využitím Newtonova gravitačního zákona napište vztahy pro velikosti sil \(F_{1}\), \(F_{2}\), \(F_{3}\) a \(F_{4}\).
Nápověda 4
Na základě obrázku (Síly působící na částici 5) a vztahů pro \(F_{1}\), \(F_{2}\), \(F_{3}\) a \(F_{4}\) určete velikost síly \(F_{5}\).
Celkové řešení
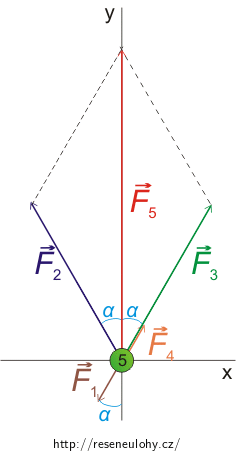
Síly působící na částici \(5\)
Na částici \(5\) působí částice \(1\) sílou \(\vec{F_{1}}\), částice \(2\) sílou \(\vec{F_{2}}\), částice \(3\) sílou \(\vec{F_{3}}\) a částice \(4\) sílou \(\vec{F_{4}}\). Celková síla působící na částici \(5\) je \(\vec{F_{5}}\).
Newtonův gravitační zákon
Dva hmotné body se navzájem přitahují stejně velkými gravitačními silami, navzájem opačného směru. Velikost gravitační síly \(F_\mathrm{g}\) je přímo úměrná součinu hmotností \(m_{1}\), \(m_{2}\) hmotných bodů a nepřímo úměrná druhé mocnině jejich vzdálenosti \(r\): \[F_\mathrm{g}=\kappa \frac{m_{1}m_{2}}{r^2},\] kde \(\kappa\) je gravitační konstanta.
Vztahy pro velikosti sil \(F_{1}\), \(F_{2}\), \(F_{3}\) a \(F_{4}\)
Částice \(1\) má hmotnost \(m_{1}\) a je od částice \(5\) o hmotnosti \(M_{5}\) vzdálena o \(2l\), velikost síly \(F_{1}\) je tedy rovna: \[F_{1}=\kappa \frac{m_{1}M_{5}}{\left(2l\right)^2}.\]
Částice \(2\) má hmotnost \(m_{2}\) a je od částice \(5\) o hmotnosti \(M_{5}\) vzdálena o \(l\), velikost síly \(F_{2}\) je tedy rovna: \[F_{2}=\kappa \frac{m_{2}M_{5}}{l^2}.\]
Částice \(3\) má hmotnost \(m_{3}\) a je od částice \(5\) o hmotnosti \(M_{5}\) vzdálena o \(l\), velikost síly \(F_{3}\) je tedy rovna: \[F_{3}=\kappa \frac{m_{3}M_{5}}{l^2}.\]
Částice \(4\) má hmotnost \(m_{4}\) a je od částice \(5\) o hmotnosti \(M_{5}\) vzdálena o \(2l\), velikost síly \(F_{4}\) je tedy rovna: \[F_{4}=\kappa \frac{m_{4}M_{5}}{\left(2l\right)^2}.\] Vidíme, že síla \(F_{1}\) má stejnou velikost jako síla \(F_{4}\) a síla \(F_{2}\) je rovna síle \(F_{3}\). Platí: \[F_{1}=F_{4}=\kappa \frac{m_{1}M_{5}}{\left(2l\right)^2},\tag{1}\] \[F_{2}=F_{3}=\kappa \frac{m_{2}M_{5}}{l^2}.\tag{2}\]
Určení velikosti síly \(F_{5}\) na základě obrázku (Síly působící na částici 5) a vztahů pro \(F_{1}\), \(F_{2}\), \(F_{3}\) a \(F_{4}\).
Síly \(\vec{F_{1}}\) a \(\vec{F_{4}}\) jsou stejné velikosti, ale mají opačné směry, proto se vyruší.
Síly \(\vec{F_{2}}\) a \(\vec{F_{3}}\) jsou stejné velikosti. Jejich x-ové složky mají opačný směr a vyruší se. Jejich y-ové složky mají stejný směr. Velikost výsledné gravitační síly \(F_{5}\) je dvojnásobkem y-ové složky \(F_{2}\) nebo \(F_{3}\): \[F_{5}=2F_{2}\cos{\alpha}=2F_{3}\cos{\alpha}.\]
Za \(F_{3}\) dosadíme dle (2): \[F_{5}=2\kappa \frac{m_{2}M_{5}}{l^2}\cos{\alpha}.\]
Číselné řešení:
Ze zadání víme:
\(m_{2}=3 \mathrm{kg}\),
\( M_{5}=9 \mathrm{kg}\),
\(l=2 \mathrm{cm}=0{,}02 \mathrm{m}\),
\(\alpha=30\mathrm{°}\).
V tabulkách dohledáme gravitační konstantu \(\kappa\):
\(\kappa \dot= 6{,}67\cdot{10}^{-11} \mathrm{\frac{m^3}{kg\cdot s^2}}\).
Dosadíme: \[F_{5}=2{\cdot} 6{,}67\cdot{10}^{-11} \frac{3{\cdot} 9}{0{,}02^2}\cos{30}\mathrm{°} \mathrm{N} \dot= 7{,}8 {\cdot} 10^{-6}\mathrm{N}= 7{,}8 \mathrm{μN}.\]
Odpověď
Výsledná gravitační síla \(\vec{F_{5}}\), kterou působí na částici \(5\) ostatní částice, má velikost:
\[F_{5}=2F_{2}\cos{\alpha}=2F_{3}\cos{\alpha}.\]
Ve zvoleném souřadném systému míří ve směru osy y.
Číselně:
\[F_{5} \dot= 7{,}8 {\cdot} 10^{-6}\mathrm{N}= 7{,}8 \mathrm{μN}.\]




