Letci a loping
Úloha číslo: 223
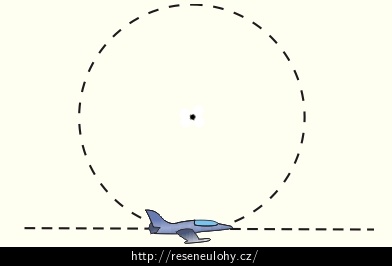
Formace tryskových letadel dělá během letecké přehlídky lopingy (viz obrázek). Jaký je minimální poloměr lopingu, jestliže letadlo v nejnižším bodě lopingu letí rychlostí 700 km·h−1 a přetížení působící na pilota v nejnižším bodě dráhy nesmí přesáhnout 6,0g?
Řešte situaci v nejnižším bodě lopingu z hlediska inerciálního i neinerciálního systému.
Zápis
amax = 6,0g maximální přetížení v = 700 km·h−1 rychlost letadla v nejnižší poloze lopingu r = ? (m) poloměr lopingu Z tabulek: g = 9,81 m·s−2 tíhové zrychlení Rozbor z hlediska inerciálního systému
Zřejmě intuitivně cítíme, že největší přetížení bude na pilota působit právě v nejnižší poloze lopingu. Víme, že právě zde na pilota nesmí působit přetížení větší než \(a_\mathrm{max}\), tedy zrychlení větší než \(a_\mathrm{max}\).
Odtud pro velikost síly, kterou působí sedačka na pilota (a tedy podle 3. Newtonova zákona i pilot na sedačku) platí, že nesmí být větší než \(ma_\mathrm{max}\).
Jde tedy o to, určit velikost síly, kterou sedačka na pilota působí.
Nápověda 1 – inerciální systém: síly
Jaké síly působí v nejnižším bodě na pilota z hlediska inerciálního systému, jaký mají tyto síly směr? Nakreslete si obrázek.
Nápověda 2 – inerciální systém: výslednice sil
Jaká je výslednice dvou zmíněných sil výše? Uvědomte si, že tato výslednice zřejmě „nutí“ letadlo i pilota k pohybu po kružnici. Jaká je velikost této výslednice?
Nápověda 3 – inerciální systém: velikost síly F
Vyjádřete ze vztahu (1) velikost síly \(\vec{F}\), kterou působí sedačka na pilota. Co po této síle (dle rozboru výše) požadujeme?
Rozbor z hlediska neinerciálního systému
Podíváme-li se na problém z hlediska neinerciálního systému, který rotuje spolu s letadlem, působí na letce setrvačná odstředivá síla \(\vec{F}_\mathrm{od}\), tíhová síla \(\vec{F}_\mathrm{G}\) a tlačí do něj sedačka silou \(\vec{F}\). Letec je vzhledem k tomuto systému v klidu, výslednice sil, které na něj působí, je tedy podle 1. Newtonova zákona rovna nule.
Pro velikost síly, kterou působí sedačka na pilota (a tedy podle 3. Newtonova zákona i pilot na sedačku), platí, že nesmí být větší než \(ma_\mathrm{max}\).
Jde tedy o to, určit velikost síly, kterou sedačka na pilota působí.
Nápověda 4 – neinerciální systém: síly
Nakreslete si obrázek znázorňující síly působící na pilota a zapište, co platí pro jejich výslednici.
Nápověda 5 – neinerciální systém: velikost síly F
Velikost síly \(\vec{F}\) vyjádřete pomocí známých vztahů pro tíhovou a odstředivou sílu. Jaká podmínka musí pro tuto velikost dle rozboru platit?
Celkové řešení
Z hlediska inerciálního systému:Z hlediska inerciálního systému působí na pilota v nejnižší poloze lopingu dvě síly:
a) Tíhová síla \(\vec{F}_\mathrm{G}\), mířící svisle dolů.
b) Reakční síla sedačky \(\vec{F}\), která míří opačným směrem, svisle vzhůru. Pro tuto sílu nám dává zadání omezení – nesmí být větší než \(ma_\mathrm{max}.\)
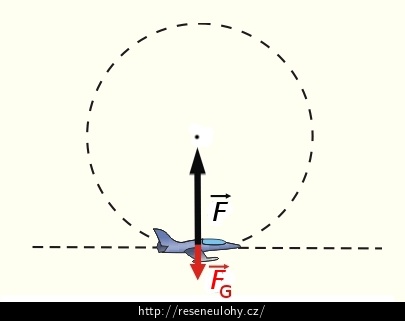
Protože pilot se s letadlem pohybuje po kružnici, jistě na něj působí dostředivá síla \(\vec{F}_\mathrm{d}\), která zakřivuje jeho trajektorii a míří do středu opisovaného lopingu. Tato dostředivá síla je výslednicí reakční síly sedačky a tíhové síly, tedy:
\[\vec{F}_\mathrm{d}\,=\,\vec{F}\,+\,\vec{F}_\mathrm{G}.\]Protože síly \(\vec{F}\) a \(\vec{F}_\mathrm{G}\) mají opačný směr, lze pro jejich velikosti psát:
\[F_\mathrm{d}\,=\,F\,-\,F_\mathrm{G}.\tag{1}\]Ze vztahu (1) dostáváme jednoduchou úpravou:
\[F\,=\,F_\mathrm{d}\,+\,F_\mathrm{G}.\]Ze znalosti vztahů pro dostředivou a tíhovou sílu můžeme psát:
\[F\,=\,m\frac{v^2}{r}\,+\,mg\,=\,m(\frac{v^2}{r}\,+\,g)\,,\]kde m je hmotnost pilota, v jeho rychlost v nejnižší poloze (zde celý problém řešíme), r poloměr opisovaného lopingu a g tíhové zrychlení.
Po této síle přitom požadujeme, aby síla byla menší nebo rovna \(ma_\mathrm{max}\), tedy:
\[F\,\leq\,ma_\mathrm{max},\] \[m(\frac{v^2}{r}\,+\,g)\,\leq\,ma_\mathrm{max}.\]Odtud dále plyne:
\[(\frac{v^2}{r}\,+\,g)\,\leq\,a_\mathrm{max},\] \[\frac{v^2}{r}\,\leq\,a_\mathrm{max}\,-\,g,\] \[r\,\geq\,\frac{v^2}{a_\mathrm{max}\,-\,g}.\]Číselně:
\[a_\mathrm{max}\,=\,6{,}0g\,=\,(6{,}0{\cdot}9{,}81)\,\mathrm{m{\cdot}s^{-2}}\,=\,58{,}86\,\mathrm{m{\cdot}s^{-2}},\] \[v\,=\,700\,\mathrm{km{\cdot}h^{-1}}\,\dot{=}\,194{,}4\,\mathrm{m{\cdot}s^{-1}},\] \[g\,=\,9{,}81\,\mathrm{m{\cdot}s^{-2}},\] \[r\,\geq\,\frac{v^2}{a_\mathrm{max}\,-\,g}\,=\,(\frac{194{,}4^2}{58{,}86\,-\,9{,}81})\,\mathrm{m}\,\dot{=}\,770\,\mathrm{m}.\]Poloměr lopingu musí být tedy minimálně 770 m.
Z hlediska neinerciálního systému:Z hlediska neinerciálního systému, který rotuje spolu s letadlem, působí na letce setrvačná odstředivá síla \(\vec{F}_\mathrm{od}\), tíhová síla \(\vec{F}_\mathrm{G}\) a tlačí do něj sedačka silou \(\vec{F}\). Letec je vzhledem k tomuto systému v klidu, výslednice sil, které na něj působí, je tedy podle 1. Newtonova zákona rovna nule:
\[\vec{F}\,+\,\vec{F}_\mathrm{G}\,+\,\vec{F}_\mathrm{od}\,=\,\vec{0}. \]Situaci v nejnižším bodě z hlediska neinerciální soustavy ukazuje obrázek níže:
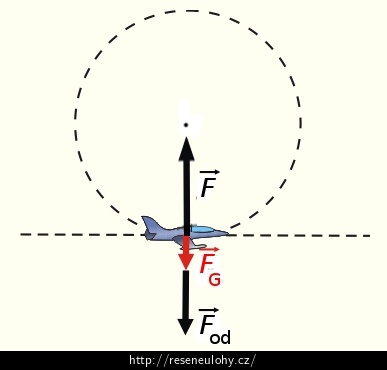
Protože tíhová a odstředivá síla mají opačný směr než síla F, kterou působí sedačka na pilota (a tedy podle 3. Newtonova zákona i pilot na sedačku), platí pro velikost síly F:
\[F\,=\,F_\mathrm{G}\,+\,F_\mathrm{od}.\]Přitom po této síle požadujeme, aby nebyla větší než \(ma_\mathrm{max}\).
S použitím známých vztahů pro odstředivou a tíhovou sílu lze psát:
\[F\,=\,F_\mathrm{G}\,+\,F_\mathrm{od}\,=\,mg\,+\,m\frac{v^2}{r}\,=\,m(g\,+\,\frac{v^2}{r}),\]kde m je hmotnost pilota, v jeho rychlost v nejnižší poloze (zde celý problém řešíme), r poloměr opisovaného lopingu a g tíhové zrychlení.
Tedy:
\[F\,\leq\,ma_\mathrm{max},\] \[m(g\,+\,\frac{v^2}{r})\,\leq\,ma_\mathrm{max},\] \[g\,+\,\frac{v^2}{r}\,\leq\,a_\mathrm{max},\] \[\frac{v^2}{r}\,\leq\,a_\mathrm{max}\,-\,g,\] \[r\,\geq\,\frac{v^2}{a_\mathrm{max}\,-\,g}.\]Dospěli jsme tedy ke stejnému vztahu jako při počítání v inerciálním systému.
Výsledek
Poloměr lopingu musí být minimálně \[r\,=\,\frac{v^2}{a_\mathrm{max}\,-\,g}\,\dot{=}\,770\,\mathrm{m}.\]




