Zubař
Úloha číslo: 915
Zubař zvedá pacientku o hmotnosti 60 kg na křesle, které má hmotnost 30 kg. Malý píst zvedacího zařízení má plochu o obsahu 5 cm2 a velký píst má plochu 200 cm2. Doktor tlačí na menší píst silou 20 N.
a) Zvedne doktor pacientku touto silou?
b) Jestliže nezvedne, urči, o kolik newtonů musí být větší síla, kterou by měl doktor působit na menší píst, aby pacientku zvedl.
Zápis
m1 = 60 kg hmotnost pacientky m2 = 30 kg hmotnost křesla S1 = 5 cm2 obsah plochy malého pístu S2 = 200 cm2 obsah plochy velkého pístu F1 = 20 N síla na malý píst Z tabulek: g = 10 N/kg číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu K části a: nápověda 1
Na jakém principu funguje zvedací zařízení zubařského křesla? A proč je tedy výhodné, aby pacientka s křeslem byla na pístu, který má větší obsah?
K části a: nápověda 2
Jaké síly působí na pacientku a křeslo a kterým působí směrem? Co musí platit pro působící síly, aby zubař pacientku s křeslem zvedl?
K části a: nápověda 3
Jak velká je gravitační síla, která působí na pacientku s křeslem?
K části a: nápověda 4
Kde se vezme síla působící na velký píst směrem nahoru?
K části a: nápověda 5
Vypočítejte velikost síly působící na velký píst.
K části a: nápověda 6
Porovnejte velikost síly F2 s velikostí gravitační síly působící na pacientku a křeslo a vytvořte závěr.
K části b: nápověda 1
Podívejte se na Nápovědu 2 v části a). Co musí platit pro velikost síly, kterou zubař musí tlačit na menší píst, aby pacientku zvedl?
K části b: nápověda 2
Vypočtěte velikost síly, kterou doktor musí tlačit na menší píst, aby pacientku zvedl a porovnejte s původní velikostí.
Poznámka
Na začátku musí doktor zatlačit o trochu více, aby křeslo s pacientkou rozjel, pak již stačí, aby byly síly vyrovnané.
Celkové řešení
Zvedací zařízení funguje na principu hydraulického lisu. Tedy malou silou (F1, viz obr.) působící na malý píst se přečerpává kapalina (zde např. olej) do většího válce a vyvolává se několikrát větší síla (F2, viz obr.) působící na velký píst. Je to proto, že tlak v kapalině, který vznikne působením vnější síly na povrch kapaliny v uzavřené nádobě, je v každém místě kapaliny stejný. A protože tlak kapaliny v nádobě vzniklý působením síly F na plochu o obsahu S je učen vztahem: \[p\,=\,\frac{F}{S},\tag{1}\]platí tedy:
\[p\,=\,\frac{F_1}{S_1}\,=\,\frac{F_2}{S_2}\]a je vidět, že na píst s větším obsahem musí působit kapalina větší silou, aby platilo, že tlak zůstává stejný.
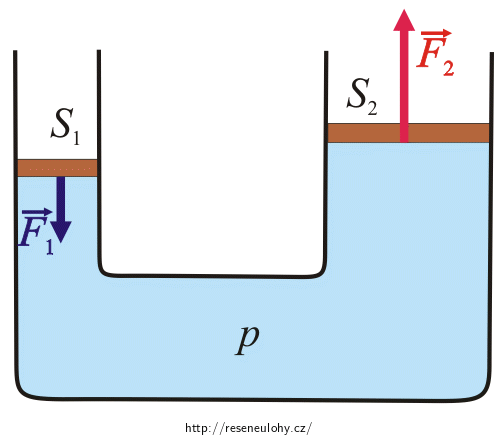
Proto doktorovi stačí na menší píst působit menší silou, aby větší píst zvedl pacientku s křeslem.
Část a)
Na pacientku a křeslo působí gravitační síla směrem dolů. Aby je šlo zvednout, musí na velký píst působit síla, která bude větší než gravitační a bude působit opačným směrem (nahoru).
Na pacientku působí gravitační síla Fg1. Její velikost vypočteme podle vzorce:
\[F_{g1}\,=\,m_1g\,.\tag{2}\]Také na křeslo působí gravitační síla o velikosti:
\[F_{g2}\,=\,m_2g\,,\tag{3}\]kde m1 je hmotnost pacientky, m2 hmotnost křesla a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu)
Výsledná gravitační síla je součtem těchto dvou sil, tedy:
\[F_g\,=\,F_{g1}\,+\,F_{g2}\,=\,(m_1\,+\,m_2)g\tag{4}\]a její velikost je po dosazení rovna Fg = 900 N.
Síla působící na velký píst směrem nahoru je způsobená tlakem, který vyvolá v kapalině doktor tím, že tlačí na malý píst silou 20 N. Pro určení její velikosti vyjdeme z rovnosti tlaku v celém objemu kapaliny (oleje). Musí platit, že tlak p vyvolaný silou doktora působící na malý píst, je všude v kapalině stejný. Tento tlak umíme vypočítat s využitím (1):
\[p\,=\,\frac{F_1}{S_1}\,.\tag{4}\]A protože víme, že tohle musí platit i pro druhý píst, tak:
\[p\,=\,\frac{F_2}{S_2}\,.\tag{6}\]Z tohoto vzorce umíme vypočítat sílu F2.
\[F_2\,=\,pS_2\,=\,\frac{F_1}{S_1}S_2.\tag{7}\]Dosadíme-li číselně, vyjde:
\[F_2\,=\,\frac{20}{5}\cdot200 \,\mathrm{N} = 800 \,\mathrm{N}\,.\]Protože gravitační síla působící na pacientku a křeslo směrem dolů je větší, než síla působící na ně směrem nahoru, zubař pacientku silou 20 N zvednout nedokáže.
Část b)
Z a) už víme, jaká gravitační síla působí na pacientku a křeslo směrem dolů. Aby je doktor zvedl, musí síla působící směrem nahoru být větší než tato síla. Dále víme, že tlak v celém objemu kapaliny se zachovává a platí pro něj (5), (6). Budeme vycházet ze situace, kdy by došlo k rovnosti sil působících na křeslo s pacientkou, tedy kdy Fg = F2n.
F2n je nová síla, s níž už doktor pacientku zvedne.
Velikost síly Fg jsme již vypočítali (900 N). Potřebujeme, aby síla F2n byla také aspoň 900 N (a jak jsme již řekli, budeme uvažovat tento krajní případ F2n = 900 N). Víme dál, že platí (5) a (6), takže i rovnost:
\[\frac{F_{1n}}{S_1}\,=\,\frac{F_{2n}}{S_2}\,. \tag{8}\]Z ní můžeme vyjádřit neznámou sílu, kterou musí doktor tlačit na menší píst:
\[F_{1n}\,=\,\frac{F_{2n}}{S_2}S_1\,. \tag{9}\]Číselně:
\[F_{1n}\,=\,\frac{900}{200}\cdot5 \,\mathrm{N} = 22{,}5 \,\mathrm{N}\,.\]Číselně dostáváme, že síla, kterou musí zubař tlačit na menší píst, je 22,5 N. Tedy o 2,5 N větší, než působil původně.
Poznámka: Na začátku musí doktor zatlačit o trochu více, aby křeslo s pacientkou rozjel, pak již stačí, aby byly síly vyrovnané.
Odpověď
a) Doktor pacientku nezvedne.
b) Doktor musí působit silou minimálně o 2,5 N větší, aby pacientku zvedl.
