Zalévání zahrady
Úloha číslo: 961
Honza napustil desetilitrovou konev za 20 sekund. Napouštěl ji na zahradě vodou z hadice. Hadice měla vnitřní průměr 19 mm a voda v ní tekla stálou rychlostí. Určete:
a) Jakou rychlostí během napouštění tekla voda v hadici?
b) Honza pak začal stříkat na brášku na druhý konec zahrady. Jakou rychlostí voda z hadice stříkala, když Honza polovinu průřezu hadice zacpal prstem? (Voda se nikde v hadici nehromadí.)
Zápis
V = 10 l = 0,01 m3 objem konve t = 20 s čas, za který Honza napustil konev d = 19 mm = 0,019 mm vnitřní průměr hadice v = ? rychlost vody při napouštění v1 = ? rychlost stříkající vody Nápověda 1 – k části a)
Jestliže voda teče hadicí stálou rychlostí v, co platí pro rychlost každé jednotlivé molekuly vody?
Nápověda 2 – k části a)
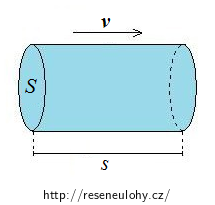
Jaké těleso tvoří voda, která proteče hadicí za 20 sekund? Napoví vám obrázek.
Nápověda 3 – k části a)
Jak určíme objem takového válce?
Nápověda 4 – k části a)
Jak určíme vzdálenost, o kterou se voda v hadici za 20 sekund posune? Uvědomte si, že se voda pohybuje rychlostí, která je stálá, nemění se. Jaký je to pohyb?
Nápověda 6 – k části a)
Co ještě potřebujeme zjistit, abychom ze vzorce (4) mohli vypočítat rychlost vody v hadici?
Nápověda 7 – k části a)
Jak určíte obsah S průřezu hadice? Vypočítejte ho.
Nápověda 8 – k části a)
Nyní už můžete dopočítat rychlost proudění vody v hadici podle (4), protože znáte všechny potřebné veličiny. Vypočtěte rychlost vody v hadici. (Nezapomeňte převést objem z litrů na metry krychlové.)
Nápověda 1 – k části b)
Co a jak se změnilo, když Honza polovinu průřezu hadice zacpal prstem?
Nápověda 2 – k části b)
Víme, že se voda nikde v hadici nehromadí. Co platí pro objem vody, která proteče za jednu sekundu různými místy hadice?
Nápověda 3 – k části b)
Víme, že objem vody proteklé za jednu sekundu musí být stejný pro různá místa hadice. Takže jak pro místo, kde ještě nebyla hadice ucpaná, tak pro místo, kde už byla polovina průřezu hadice ucpaná Honzovým prstem. V této části hadice se průřez změnil na poloviční. Co se ještě muselo v této části změnit? Využijte vzorec (1) a (2) z části a).
Nápověda 4 – k části b)
Jak se změní rychlost průtoku vody, když se hadice zúží? Využijte vzorec (4).
Nápověda 5 – k části b)
Jak se změní rychlost průtoku vody, když se průřez zmenší na polovinu?
Nápověda 6 – k části b)
Určete velikost nové rychlosti číselně.
Komentář
Část b) lze řešit (na úrovni SŠ) obecně pomocí rovnice kontinuity. Oběma průřezy musí za daný čas t protéct stejný objem vody. Platí tedy:
\[V = V_1\,,\] \[S{\cdot}v{\cdot}t\,=\,S_1{\cdot}v_1{\cdot}t\,,\] \[S{\cdot}v\,=\,S_1{\cdot}v_1\,.\]Odtud:
\[v_1\,=\,\frac {S{\cdot}v}{\frac{S}{2}}\,=\,2{\cdot}v\,.\]Celkové řešení
Řešení části a):Jestliže voda teče hadicí stálou rychlostí v, tak také každá molekula (část) vody se pohybuje touto rychlostí.
Voda, která proteče hadicí za 20 sekund, tvoří válec.

Tento válec má obsah podstavy S rovný obsahu průřezu hadice. Výška válce je rovna dráze s, kterou voda (vybraná molekula nebo část vody) urazí za těch 20 sekund.
Objem takového válce určíme podle vzorce:
\[V\,=\,S{\cdot}s\,,\tag{1}\]kde S je průřez hadice (resp. jeho obsah) a s je vzdálenost, o kterou se voda posune za 20 sekund.
Voda se pohybuje rovnoměrným pohybem, pro jeho dráhu platí:
\[s\,=\,v{\cdot}t\,,\tag{2}\]kde v je rychlost tohoto pohybu a t doba pohybu (v našem případě 20 s).
Dosazením (2) do (1) získáme:
\[V\,=\,S {\cdot} v{\cdot} t\,,\tag{3}\]kde S je průřez hadice (resp. jeho obsah), v je rychlost, kterou voda teče, a t doba pohybu vody (v našem případě 20 s).
Vyjádříme neznámou rychlost v:
\[v\,=\,\frac {V}{S{\cdot} t}\,,\tag{4}\]kde V je objem vody, která proteče hadicí za 20 sekund, S je průřez hadice (resp. jeho obsah) a t doba pohybu vody (v našem případě 20 s).
Abychom mohli rychlost vody dopočítat, potřebujeme zjistit ještě obsah S průřezu hadice.
Obsah průřezu hadice spočítáme jako obsah kruhu o známém průměru d:
\[S\,=\,\frac {\pi{\cdot} d^2}{4}\,.\tag{5}\]Číselně:
\[S\,=\,\frac {\pi{\cdot} 0{,}019^2}{4} \mathrm{m}^2\,\dot=\,0{,}00028\,\mathrm{m}^2\,.\]Teď už můžeme dosadit do (4) a dopočíst rychlost vody v hadici:
\[v\,=\,\frac {V}{S{\cdot} t}\,.\]Číselně:
\[v\,=\,\frac {0{,}01}{0{,}00028{\cdot} 20}\,\mathrm{m\cdot s^{-1}}\,\dot=\,1{,}8\,\mathrm{m\cdot s^{-1}}\,.\]Řešení části b):
Aby se voda v hadici nikde nehromadila, musí za jednu sekundu protéct různými místy hadice vždy stejný objem vody. To muselo platit jak v místě, kde ještě nebyla hadice ucpaná, tak i v místě, kde už byla část hadice ucpaná Honzovým prstem. Když Honza zacpal hadici prstem, zmenšil se v tom místě obsah jejího průřezu na poloviční.
Ze vzorce (1) je vidět, že aby objem proteklé vody zůstal zachován, tak se při změně průřezu S musí změnit také dráha s. Ta je určena vzorcem s = v·t .
Čas t se nemění. Aby se měnila dráha s, musí se měnit rychlost v.
Ze vzorce (4) je vidět, že když se zmenší obsah průřezu hadice S, zmenší se jmenovatel zlomku, takže dělíme menším číslem – rychlost se zvětší.
Dál je ze vztahu (4) vidět, že když se průřez zmenší na polovinu, budeme dělit polovičním číslem, dostaneme tedy dvakrát větší hodnotu rychlosti. Voda tedy v místě zúžení hadice prstem na polovinu poteče dvakrát větší rychlostí.
Když Honza polovinu průřezu hadice ucpal prstem, byla nová rychlost vody:
\[v_1\,=\,\frac{V}{S_1\cdot t}\,,\tag{6}\]kde S1 je polovina S z části a).
Číselně:
\[v\,=\,\frac {0{,}01}{0{,}00014{\cdot} 20}\,\mathrm{m\cdot s^{-1}}\,\dot=\,3{,}6\,\mathrm{m\cdot s^{-1}}\,.\]Odpověď
a)
\[v\,=\,\frac{V}{S\cdot t}\,\,\dot=\,1{,}8\,\mathrm{m\cdot s^{-1}}\]Během napouštění tekla voda v hadici rychlostí přibližně 1,8 m·s−1.
b)
\[v_1\,=\,\frac{V}{S_1\cdot t}\,\,\dot=\,3{,}6\,\mathrm{m\cdot s^{-1}}\]Když Honza polovinu průřezu hadice zacpal prstem, stříkala voda z hadice rychlostí přibližně 3,6 m·s−1.



