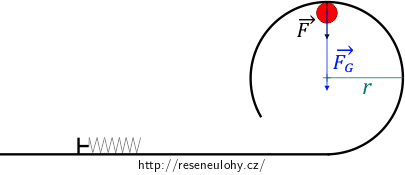
Kulička vystřelená na válcovou plochu
Úloha číslo: 2210
Kuličku můžeme vystřelovat pomocí stlačené pružiny po dráze zakončené válcovou plochou (viz obr. 1). Určete, o kolik centimetrů nejméně musíme stlačit pružinu tuhosti \(k\), aby kulička hmotnosti \(m\) projela celou kruhovou smyčku o poloměru \(r\). Tření, odpor vzduchu a moment setrvačnosti kuličky zanedbejte.
Řešte nejprve obecně, potom pro hodnoty \(k = 20\,\mathrm{Nm^{-1}},\, m = 10\,\mathrm{g},\, r = 10\,\mathrm{cm},\, g = 9{,}81\,\mathrm{ms^{-2}}.\)
Zápis úlohy, nákres situace
\(k = 20\,\mathrm{Nm^{-1}}\)…tuhost pružiny
\(m = 10\,\mathrm{g} = 0{,}01\,\mathrm{kg}\)…hmotnost kuličky
\(r = 10\,\mathrm{cm} = 0{,}1\,\mathrm{m}\)…poloměr válcové plochy
\(g = 9{,}81\,\mathrm{ms^{-2}}\)…gravitační zrychlení
\(x =\,?\,\)…nejmenší délka dostatečného stlačení pružiny

Rozbor
Budeme předpokládat, že veškerá potenciální energie pružnosti stlačené pružiny se při vystřelení předá kuličce. Kulička tím získá určitou kinetickou energii. Ta se při průjezdu válcovou plochou mění na potenciální. V nejvyšším bodě smyčky kulička nemůže mít nulovou rychlost, to by spadla. Musíme zjistit minimální rychlost, při které kulička ještě dráhu projede. Ta odpovídá minimálnímu stlačení pružiny. Rozmyslíme, jaké síly působí na kuličku a jak je to s jejich velikostí pro kritickou situaci. Z pohybové rovnice pak zjistíme minimální rychlost.
K řešení úlohy dále využijeme zákon zachování mechanické energie. Zvolíme hladinu nulové potenciální energie a dvě situace, ve kterých napíšeme, čemu je rovna mechanická energie kuličky. Z jejich rovnosti pak vyjádříme hledané stlačení pružiny. Jako první situaci zvolíme okamžik těsně poté, co se kulička odpoutá od pružiny. Jako druhou okamžik, kdy kulička projíždí nejvyšším bodem smyčky.
Nápověda 1
Rozmyslete si, jaké síly působí na kuličku v nejvyšším bodě smyčky a jaká je jejich velikost pro různé rychlosti kuličky. Co bude platit pro nejmenší rychlost \(v\), kterou se kulička může pohybovat v nejvyšším bodě smyčky, aby ještě nespadla?
Nápověda 2
Předpokládejte, že stlačená pružina předá veškerou svou energii kuličce. Připomeňte si vztah pro potenciální energii pružnosti pružiny. K dalšímu řešení využijte zákon zachování mechanické energie. Zvolte nulovou hladinu potenciální energie a zapište si, jaká je mechanická energie kuličky poté, co se odpoutá od pružiny, a v nejvyšším bodě smyčky.
Obecné řešení
Aby kulička ve smyčce nespadla, musí mít dostatečnou rychlost v nejvyšším bodě smyčky. Na kuličku v nejvyšším bodě působí tíhová síla \(F_\mathrm{G}\), jejíž velikost na rychlosti kuličky nezávisí, a tlačí do ní smyčka silou \(F\). Výslednice těchto sil uděluje kuličce příslušné dostředivé zrychlení \(a_\mathrm{d}\).
Pohybová rovnice pro kuličku v nejvyšším bodě je tedy:
\[ F_\mathrm{G} + F = ma_\mathrm{d} = m\frac{v^2}{r}, \]
kde \(v\) je rychlost, kterou se kulička pohybuje, a \(r\) je poloměr kruhové dráhy.
Pohybuje-li se kulička větší rychlostí, musí na ni smyčka zatlačit více, aby její trajektorii zakřivila. Při menší rychlosti stačí, aby tlačila méně. Minimální rychlost, a tedy i minimální stlačení pružiny, bude odpovídat situaci, kdy smyčka přestane do kuličky tlačit a síla \(F\) bude nulová. Platí tedy:
\[F_\mathrm{G} = ma_\mathrm{d} = m\frac{v_\mathrm{min}^2}{r},\] \[mg = m\frac{v_\mathrm{min}^{2}}{r}.\]Odtud vyjádříme nejmenší možnou rychlost kuličky
\[v_\mathrm{min} = \sqrt {gr}.\tag{1}\]
K řešení úlohy dále využijeme zákon zachování mechanické energie (ZZME). Porovnáme celkovou mechanickou energii kuličky poté, co se odpoutá od pružiny, a v nejvyšším bodě smyčky.
Předpokládáme, že při vystřelení pružina předá kuličce veškerou svou potenciální energii pružnosti \(E_\mathrm{pr}\), která závisí na délce stlačení pružiny \(x\) a její tuhosti \(k\). Počáteční kinetická energie kuličky \(E_\mathrm{k1}\)bude tedy rovna potenciální energii pružnosti pružiny.
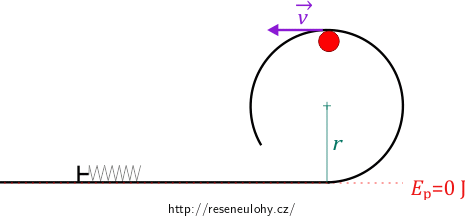
Pokud zvolíme nulovou hladinu potenciální energie \(E_\mathrm{p}\) v úrovni pružiny (a počáteční polohy kuličky), nachází se kulička při průchodu nejvyšším bodem smyčky ve výšce \(2r\) (viz obr). Má tedy nenulovou potenciální energii. Zároveň se pohybuje rychlostí \(v_\mathrm{min}\), má tedy i kinetickou energii \(E_\mathrm{k2}\). Podle ZZME platí:
\[ E_\mathrm{pr} = E_\mathrm{k1} = E_\mathrm{p} + E_\mathrm{k}, \]
\[ \frac{1}{2}kx^2 = 2mgr + \frac{1}{2}mv_\mathrm{min}^2. \]
Za rychlost \(v_\mathrm{min}\) dosadíme ze vztahu (1) a vyjádříme neznámou \(x\):
\[ \frac{1}{2}kx^2 = 2mgr + \frac{1}{2}m\sqrt {gr}^2, \]
\[ kx^2 = 4mgr + mgr, \]
\[ x = \sqrt {\frac{5mgr}{k}}. \tag{2}\]
Tím jsme určili nejmenší délku stlačení pružiny obecně.
Výpočet
Dosadíme do odvozeného vztahu (2) podle hodnot v zadání, které správně převedeme na základní jednotky:
\[ x = \sqrt {\frac{5 {\cdot} 0{,}01 {\cdot} 9{,}81 {\cdot} 0{,}1 }{20}} \,\mathrm {m} = 0{,}05\,\mathrm {m} = 5\,\mathrm {cm}. \]
Odpověď
Nejmenší stlačení pružiny je \(5\,\mathrm {cm}\), obecně jej určíme jako
\[ x = \sqrt {\frac{5mgr}{k}}. \]
K zamyšlení
A jak by to bylo ve skutečnosti? Kdybychom si takovou dráhu vyrobili, použili prvky s parametry podle zadání a experiment provedli přesně podle našich výpočtů, jaký by byl výsledek? Myslíte, že by kulička smyčkou projela, nebo by spadla?