Pračlověk a síly

Úloha číslo: 220

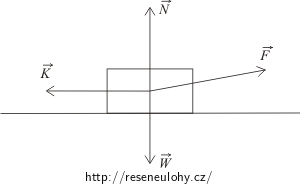
Pračlověk táhne kořist do své jeskyně konstantní rychlostí působením síly \(\vec{F}\) (viz obrázek). Táhne ji rovně po drsném vodorovném povrchu. Šipky na obrázku ukazují směr sil působících na kořist. Jaký platí vztah mezi velikostmi uvedených sil?

Nápověda 1 – význam jednotlivých sil
Interpretujte význam ostatních sil na obrázku a popište příčiny jejich vzniku.
Řešení k nápovědě 1
Síla \(\vec{K}\) vzniká v důsledku tření kořisti s drsným povrchem a působí proti směru pohybu.

Síla \(\vec{W}\) je síla tíhová, míří svisle dolů a jejím původcem je tíhové pole Země.

Silou \(\vec{N}\) tlačí povrch kolmo vzhůru na kořist (kořist spočívající na povrchu na něj kolmo dolů tlačí a podle 3. Newtonova zákona působí stejně velkou, opačně orientovanou silou i povrch na kořist).
Nápověda 2 – druh pohybu, 1. Newtonův zákon
Jakým pohybem se tažená kořist pohybuje? Jaká musí být při tomto pohybu podle 1. Newtonova zákona výslednice sil, které na kořist působí?
Řešení k nápovědě 2
Podle zadání je rychlost, kterou je kořist tažena, konstantní. Jde tedy o pohyb rovnoměrný a můžeme předpokládat, že také přímočarý. Má-li se ale těleso pohybovat rovnoměrným přímočarým pohybem, musí být dle 1. Newtonova zákona výslednice sil na něj působících nulová (nulový vektor), tedy:
\[\vec{K}\,+\,\vec{N}\,+\,\vec{W}\,+\,\vec{F}\,=\,\vec{o}.\]
Nápověda 3 – rozklad síly F
Rozložte sílu \(\vec{F}\) na vodorovnou složku (\(\vec{F}_1\)) a svislou složku (\(\vec{F}_2\)). Co nyní platí – opět podle 1. Newtonova zákona – pro síly rovnoběžné s povrchem a pro síly kolmé k povrchu?
Řešení k nápovědě 3
Rozklad síly \(\vec{F}\) na vodorovnou složku \(\vec{F}_1\) a svislou složku \(\vec{F}_2\) ukazuje obrázek níže:

Z něj je také patrné, že aby byla výslednice všech sil nulová, musí být nulová jak výslednice ve vodorovném, tak ve svislém směru, tedy:
\[\vec{K}\,+\,\vec{F}_1\,=\,\vec{o},\] \[\vec{N}\,+\vec{W}\,+\,\,\vec{F}_2\,=\,\vec{o}.\]
Přitom je vidět, že:

a) síla \(\vec{K}\) má opačný směr než síla \(\vec{F}_1,\)

b) síly \(\vec{F}_2\) a \(\vec{N}\) mají opačný směr než síla \(\vec{W}.\)

Odtud tedy pro velikosti sil (v zápisu je od vektorů odlišujeme tak, že již nepíšeme vektorové šipky) platí:

a) \[K\,=\,F_1,\tag{1}\]

b) \[N\,+\,F_2\,=\,W.\tag{2}\]
Nápověda 4
Rovnice (1) a (2) výše lze vlastně již považovat za formu výsledku, ale ještě by se nám líbilo, kdyby ve výsledku vystupovaly pouze síly ze zadání, tedy ne složky. Vyjádřete proto velikost složek \(F_1\), \(F_2\) pomocí velikosti síly \(F\). Dosaďte do rovnic (1) a (2) a vyjádřete nerovnostmi vztahy mezi silami ze zadání.
Řešení k nápovědě 4
Úhel mezi vektory \(\vec{F}\) a \(\vec{F}_1\) označme α. Potom pro velikosti složek síly \(\vec{F}\) platí:
\[F_1\,=\,F\cos{\alpha},\] \[F_2\,=\,F\sin{\alpha}.\]
Rovnice (1) a (2) lze nyní přepsat:
\[K\,=\,F\cos{\alpha},\] \[N\,+\,F\sin{\alpha}\,=\,W.\]
Protože zjevně \(0^{\circ}\,\lt\,\alpha\,\lt\,90^{\circ}\), nabývají obě goniometrické funkce kladných hodnot menších než 1 a platí:
\[K\,\lt\,F,\] \[N\,\lt\,W.\]
Celkové řešení
Podle zadání je rychlost, kterou je kořist tažena, konstantní. Jde tedy o pohyb rovnoměrný a můžeme předpokládat, že také přímočarý. Má-li se ale těleso pohybovat rovnoměrným přímočarým pohybem, musí být dle 1. Newtonova zákona výslednice sil na něj působících nulová (nulový vektor), tedy:
\[\vec{K}\,+\,\vec{N}\,+\,\vec{W}\,+\,\vec{F}\,=\,\vec{o}.\]
Sílu \(\vec{F}\) můžeme rozložit na vodorovnou složku \(\vec{F}_1\) a svislou složku \(\vec{F}_2\). Tento rozklad ukazuje obrázek níže:

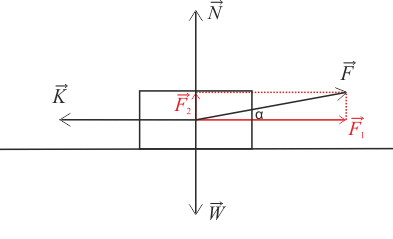
Z něj je také patrné, že aby byla výslednice všech sil nulová, musí být nulová jak výslednice ve vodorovném, tak ve svislém směru, tedy:
\[\vec{K}\,+\,\vec{F}_1\,=\,\vec{o},\] \[\vec{N}\,+\vec{W}\,+\,\,\vec{F}_2\,=\,\vec{o}.\]
Přitom je vidět, že:

a) síla \(\vec{K}\) má opačný směr než síla \(\vec{F}_1,\)

b) síly \(\vec{F}_2\) a \(\vec{N}\) mají opačný směr než síla \(\vec{W}\).

Odtud tedy pro velikosti sil (v zápisu je od vektorů odlišujeme tak, že již nepíšeme vektorové šipky) platí:

a) \[K\,=\,F_1,\tag{1}\]

b) \[N\,+\,F_2\,=\,W.\tag{2}\]

Na závěr vyjádříme velikost složek \(\vec{F}_1\) a \(\vec{F}_2\) pomocí velikosti síly \(\vec{F}\). Úhel mezi vektory \(\vec{F}\) a \(\vec{F}_1\) označme α. Potom pro velikosti složek síly \(\vec{F}\) platí:
\[F_1\,=\,F\cos{\alpha},\] \[F_2\,=\,F\sin{\alpha}.\]
Rovnice (1) a (2) lze nyní přepsat:
\[K\,=\,F\cos{\alpha},\] \[N\,+\,F\sin{\alpha}\,=\,W.\]
Protože zjevně \(0^\circ\,\lt\,\alpha\,\lt\,90^\circ\), nabývají obě goniometrické funkce kladných hodnot menších než 1 a platí:
\[K\,\lt\,F,\] \[N\,\lt\,W.\]
Výsledek
Pro síly ze zadání platí:
\[K\,\lt\,F,\] \[N\,\lt\,W.\]
Konkrétně:
\[K\,=\,F\cos{\alpha},\] \[N\,+\,F\sin{\alpha}\,=\,W.\]
Kde α je úhel mezi vektory \(\vec{F}\) a \(\vec{F}_1\), \(0^\circ\,\lt\,\alpha\,\lt\,90^\circ.\)