Ohyb nosníku
Úloha číslo: 2158
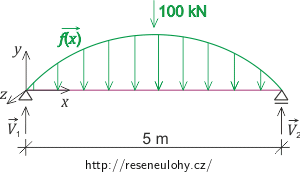
Na obrázku je ocelový nosník délky 5 m obdélníkového průřezu, kde vodorovný rozměr je 0,1 m a svislý 0,2 m. Modul pružnosti v tahu je 200 GPa. Nosník je po celé délce spojitě zatížen svisle dolů zatížením, jehož lineární hustota je ve tvaru funkce sinus v prvních dvou kvadrantech tak, že celkové zatížení je 100 kN. Zatížení míří k těžišti průřezu. Na oba jeho konce působí vazbové síly, při nichž je nosník v rovnováze. Důsledkem toho dojde k deformaci původně přímého tvaru nosníku. Určete funkci popisující podélný tvar nosníku po deformaci, tedy ohybový průběh. Vlastní tíhu nosníku zanedbejte.
Zápis
l = 5 m délka nosníku a = 0,1 m vodorovný rozměr průřezu b = 0,2 m svislý rozměr průřezu E = 200 GPa modul pružnosti v tahu F = 100 kN celkové zatížení y(x) = ? ohybový průběh Rozbor
Nejprve je třeba určit vazbové síly tak, aby nosník byl v rovnováze. Dále bude potřeba určit průběh momentů sil podél nosníku. Pro další postup se musí vypočítat kvadratický moment průřezu. Nakonec bude zbývat vyřešit diferenciální rovnici pro ohyb a u toho uvažovat vhodné počáteční podmínky.
Nápověda
Nejprve určete vazbové síly pro podmínku rovnováhy. Funkci lineární hustoty zatížení určete tak, aby jeho integrál přes celou délku byl roven celkovému zatížení. Dále bude potřeba určit průběh momentů sil podél nosníku. Odvoďte si pro něj pravidlo per partes. Jestliže si tento průběh vyjádříte v závislosti na x, pak si toto x nějak označte, aby se tato proměnná dále nepletla s proměnnou pro průběh deformace, tedy ohybu. V průběhu momentů uvažujte celkový moment od sil vždy před proměnnou. Pokračujte výpočtem kvadratického momentu průřezu. Nakonec použijte příslušnou diferenciální rovnici. V rovnici uvažujte počáteční podmínky. Počáteční podmínky plynou z poloh konců nosníku a ze symetrie, díky které dochází k největšímu ohybu uprostřed nosníku.
Řešení
Nejprve je třeba určit vazbové síly, aby nosník byl v rovnováze. To znamená, že musí být splněna rovnice:
\[V_1+V_2\,=\,F,\tag{1}\]kde V1 je vazbová síla na levém konci nosníku a V2 je vazbová síla na pravém konci nosníku. V rovnici (1) není zahrnuta vlastní tíha nosníku, kterou budeme uvažovat za zanedbatelnou. Ze symetrie je hned vidět, že platí:
\[V_1\,=\,V_2\,=\,\frac{F}{2}.\tag{2}\]Bude potřeba zjistit průběh lineární hustoty zatížení. Podle zadání je lineární hustota zatížení funkcí sinus na prvních dvou kvadrantech. Jedná se tedy o funkci:
\[f(x)\,=\,A\sin{(\frac{\pi x}{l})},\tag{3}\]kde A je pro nás zatím neznámá konstanta. Ovšem integrací (3) přes celou délku nosníku dostaneme celkové zatížení, takže platí:
\[F\,=\,\int_{0}^{l}A\sin{(\frac{\pi x}{l})}\mathrm{d}x\,=\,\frac{2Al}{\pi}.\tag{4}\]Ze (4) vyjádříme:
\[A\,=\,\frac{F\pi}{2l}\tag{5}\]a z (5) dosadíme do (3), takže vznikne:
\[f(x)\,=\,\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}.\tag{6}\]Dále budeme určovat průběh momentů, který bude funkcí závislou na x, avšak bude potřeba si tuto proměnnou označit například s čárkou. Tento průběh uvažuje pouze momentové síly před tím bodem nosníku, ve kterém moment počítáme. Kdybychom uvažovali momentové síly i za tímto bodem, pak by celkový moment byl samozřejmě nulový, protože nosník máme v rovnováze. K porozumění může posloužit obrázek.

Momentový průběh dle obrázku, kde nás zajímají červeně vyznačené síly, zapíšeme ve tvaru:
\[M(x')\,=\,-\frac{F}{2}x'+\left(\int_{0}^{x'}\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x\right)t(x'),\tag{7}\]kde t je vzdálenost mezi těžištěm na obrázku červeně vyznačené oblasti lineární hustoty zatížení a bodem, vůči kterému moment počítáme. To vypočítáme vztahem:
\[t(x')\,=\,x'-\frac{\int_{0}^{x'}x\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x}{\int_{0}^{x'}\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x}.\tag{8}\](8) dosadíme do (7), takže:
\[M(x')\,=\,-\frac{F}{2}x'+\left(\int_{0}^{x'}\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x\right)x'-\int_{0}^{x'}x\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x.\tag{9}\]Integrál z druhého členu v rovnici (9) je:
\[\int_{0}^{x'}\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x\,=\,-\frac{F}{2}\left(\cos{(\frac{\pi x'}{l})}-1\right).\tag{10}\]Dosazením (10) do (9) získáme:
\[M(x')\,=\,-\frac{F}{2}\cos{(\frac{\pi x'}{l})}x'-\int_{0}^{x'}x\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x.\tag{11}\]Nyní pomocí pravidla per partes (získá se tak, že se derivuje součin dvou funkcí a potom se zpětně integruje) upravíme druhý člen v (11), tedy:
\[\int_{0}^{x'}x\frac{F\pi}{2l}\sin{(\frac{\pi x}{l})}\mathrm{d}x\,=\,-\frac{F}{2}\cos{(\frac{\pi x'}{l})}x'+\frac{Fl}{2\pi}\sin{(\frac{\pi x'}{l})}.\tag{12}\]Dosazením (12) do (11) už konečně dostaneme:
\[M(x')\,=\,-\frac{Fl}{2\pi}\sin{(\frac{\pi x'}{l})}.\tag{13}\]Teď potřebujeme vypočítat kvadratický moment průřezu I. S ohledem na to, že průřez je obdélníkový, využijeme vztah:
\[I\,=\,\int_{-\frac{a}{2}}^{\frac{a}{2}}\int_{-\frac{b}{2}}^{\frac{b}{2}}y^2\mathrm{d}y\mathrm{d}z\,=\,\frac{ab^3}{12}.\tag{14}\]Můžeme už přejít k diferenciální rovnici pro ohyb:
\[\frac{\mathrm{d}^2y(x)}{\mathrm{d}x^2}\,=\,-\frac{M(x')}{EI}.\tag{15}\]Rovnici (15) najdete v běžně dostupné literatuře týkající se dané oblasti, ovšem je třeba dávat pozor na znaménko. To závisí nejen na orientaci os, ale i na tom, zda momentový průběh uvažujeme zleva doprava, či obráceně. Když zintegrujeme (15), dostaneme:
\[\frac{\mathrm{d}y(x)}{\mathrm{d}x}\,=\,-\frac{M(x')}{EI}x+B,\tag{16}\]kde B je konstanta. Jelikož je kvůli symetrii zřejmé, že k největšímu ohybu, tedy k extrému, dojde uprostřed nosníku, musí platit:
\[0\,=\,-\frac{M(x')}{EI}\frac{l}{2}+B,\]tedy:
\[B\,=\,\frac{M(x')}{EI}\frac{l}{2}.\tag{17}\]Dosazením (17) do (16) získáme:
\[\frac{\mathrm{d}y(x)}{\mathrm{d}x}\,=\,-\frac{M(x')}{EI}x+\frac{M(x')}{EI}\frac{l}{2}.\tag{18}\]Po integraci (18) je:
\[y(x)\,=\,-\frac{M(x')}{EI}\frac{x^2}{2}+\frac{M(x')}{EI}\frac{l}{2}x+C.\tag{19}\]Abychom vyjádřili konstantu C, stačí si uvědomit, že pro x rovno 0 nebo l kvůli vazbám na koncích k žádnému svislému posunutí nedojde, takže platí:
\[C\,=\,0.\tag{20}\]Rovnice popisující ohyb nosníku je:
\[y(x)\,=\,-\frac{M(x')}{EI}\frac{x^2}{2}+\frac{M(x')}{EI}\frac{l}{2}x\,=\,\frac{M(x')}{EI}\left(\frac{l}{2}x-\frac{x^2}{2}\right).\tag{21}\]Po dosazení ze (13) a (14) máme:
\[y(x)\,=\,-\frac{6Fl}{ab^{3}E\pi}\sin{(\frac{\pi x'}{l})}\left(\frac{l}{2}x-\frac{x^2}{2}\right).\tag{22}\]Záporné znaménko je dáno tím, že jsme si osu z orientovali směrem nahoru, zatímco nosník se prohýbá směrem dolů. Dále už nebude potřeba oddělovat x s čárkou od x bez čárky. Nyní už pouze číselně dosadíme do (22), nakonec tedy vyjde:
\[y(x)\,=\,-\frac{6{\cdot}100\cdot10^3{\cdot}5}{0{,}1{\cdot}0{,}2^{3}\cdot200{\cdot}10^9\cdot\pi}\sin{(\frac{\pi x}{5})}\left(\frac{5}{2}x-\frac{x^2}{2}\right)\mathrm{m}\doteq -6{\cdot}10^{-3}\sin{(\frac{\pi x}{5})}\left(\frac{5}{2}x-\frac{x^2}{2}\right)\mathrm{m}.\]Odpověď
Ohybový průběh nosníku je:
\[y(x)\doteq -6{\cdot}10^{-3}\sin{(\frac{\pi x}{5})}\left(\frac{5}{2}x-\frac{x^2}{2}\right)\mathrm{m}.\]

