Tyč opřená o schod
Úloha číslo: 525
Zápis
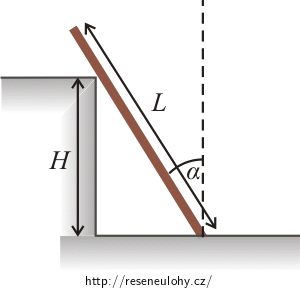
L délka tyče m hmotnost tyče H výška schodu α úhel, který svírá tyč se svislým směrem T = ? velikost třecí síly u podlahy ? velikost a směr dalších sil, kterými působí schod a podlaha na tyč Nápověda 1
Jaké síly působí na tyč? Zakreslete je do obrázku.Nápověda 2
Co platí pro síly a momenty sil, je-li tyč v rovnováze?Nápověda 3
Zapište si podmínky rovnováhy a přepište je skalárně.
Nápověda 4:
Vyjádřete vzdálenost R a z rovnic (1), (2) a (3) pak hledané síly.
Celkové řešení
Nakreslíme obrázek a vyznačíme působící síly.
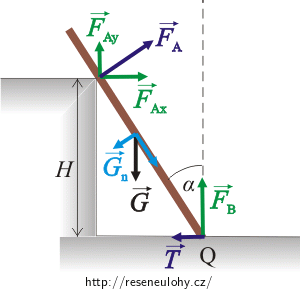
Na tyč působí v těžišti tíhová síla \(\vec{G} = m \vec{g}\).
Podlaha na tyč jednak tlačí kolmo vzhůru silou \(\vec{F}_\mathrm{B}\), jednak na ni směrem doleva působí třecí silou \(\vec{T}\), která brání sklouznutí. Schod tlačí silou \(\vec{F}_\mathrm{A}\) kolmo na tyč.
Působící síly udržují tyč v rovnováze. Znamená to, že výslednice sil působících na tyč musí být nulová a také výslednice momentů těchto sil musí být rovna nule (vzhledem k libovolnému bodu).
Výslednice sil je nulová:
\[\vec{F}_\mathrm{A}+\vec{F}_\mathrm{B}+\vec{G}+\vec{T} = \vec{0}\,.\]Zvolíme obvyklou soustavu souřadnic (x je kladné doprava, y je kladné nahoru) a přepíšeme skalárně:
\[ x:\hspace{50px} F_\mathrm{Ax} = T\,,\] \[y:\hspace{10px} F_\mathrm{Ay}+F_\mathrm{B} = G\,.\]Pro složky síly \(\vec{F}_\mathrm{A}\) platí:
\[F_\mathrm{Ax} = F_\mathrm{A} \cos \alpha\,,\] \[F_\mathrm{Ay} = F_\mathrm{A} \sin \alpha\,.\]A tedy:
\[ F_\mathrm{A} \cos \alpha = T\,,\tag{1}\] \[ F_\mathrm{A} \sin \alpha + F_\mathrm{B} = G\,.\tag{2}\]Výslednice momentů sil je vzhledem k libovolnému bodu nulová:
\[\vec{M}_\mathrm{G}+\vec{M}_\mathrm{A}+\vec{M}_\mathrm{B}+\vec{M}_\mathrm{T} = \vec{0}\,.\]Připomeňme si ještě vztah pro moment síly \(\vec{F}\) vzhledem k bodu O:
\[\vec{M} = \vec{r} \times \vec{F}\,.\]Pro velikost momentu platí: \(M = rF\sin \varphi\), kde \(\varphi\) je úhel, který svírají vektory \(\vec{r}\) a \(\vec{F}\).
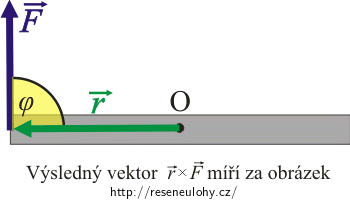
Směr momentu síly je kolmý na rovinu, ve které leží vektory \(\vec{r}\) a \(\vec{F}\). Orientace se určí pomocí pravidla pravé ruky: prsty dáme tak, aby směřovaly od \(\vec{r}\) k \(\vec{F}\), napnutý palec pak ukazuje směr vektoru \(\vec{M}\).
Momenty sil budeme určovat vůči bodu Q, kde tyč stojí na zemi. Tím vynulujeme momenty sil, které působí v daném bodě (\(\vec{r}_\mathrm{T} = \vec{0}\) a \(\vec{r}_\mathrm{B} = \vec{0}\)).
Zbývá:
\[ \vec{M}_\mathrm{G} + \vec{M}_\mathrm{A} = \vec{0}\,.\]Za záporný směr otáčení zvolíme směr otáčení hodinových ručiček, momenty sil mířící „za papír“ budeme uvažovat jako záporné. Pak
\[ M_\mathrm{G} - M_\mathrm{A} = 0\,.\]Pro velikosti momentů platí:
\[ \frac{L}{2} G \sin \alpha - RF_\mathrm{A} = 0\,,\tag{3}\]kde R je vzdálenost bodu Q od působiště síly \(\vec{F}_\mathrm{A}\).
Vzdálenost působiště síly FA od Q spočítáme z trojúhelníku, jehož strany tvoří podlaha, tyč a boční strana schodu. Úhel mezi schodem a tyčí je α, takže
\[R=\frac{H}{\cos \alpha}\,.\]Zbytek je jednoduchá matematika. Z (3) dostáváme:
\[F_\mathrm{A}=GL \frac{\sin \alpha} {2R}\,.\]Dosadíme za R:
\[F_\mathrm{A}=GL \frac{\sin \alpha \cos \alpha} {2H}\,.\]Z (1):
\[T= F_\mathrm{A} \cos \alpha = GL \frac{\sin \alpha \cos^2\alpha}{2H}\,.\]Zbývá síla FB, kterou získáme dosazením FA do (2):
\[F_\mathrm{B}=G -GL \frac{\sin^2\alpha \cos \alpha}{2H}\,.\]Výsledky lze ještě upravit pomocí \[\sin(2\alpha)=2 \sin \alpha \cos \alpha\,,\]
\[F_\mathrm{A}=GL \frac{\sin 2\alpha} {4H}\,,\] \[F_\mathrm{B}=G-GL \frac{\sin 2\alpha \sin \alpha} {4H}\,,\] \[T=GL \frac{\sin 2\alpha \cos \alpha} {4H}\,.\]Odpověď:
Pro velikosti působících sil platí:
\[F_\mathrm{A}=GL \frac{\sin 2\alpha} {4H}\,,\] \[F_\mathrm{B}=G-GL \frac{\sin 2\alpha \sin \alpha} {4H}\,.\] \[T=GL \frac{\sin 2\alpha \cos \alpha} {4H}\,.\]Směr těchto sil ukazuje obrázek.

Podobná úloha
Vyřešeno? Zkuste podobnou úlohu Opřený žebřík.




