Záhadný kov
Úloha číslo: 935
Při archeologických vykopávkách nalezl jeden archeolog úlomek neznámého kovu. Chtěl zjistit, o jaký kov se jedná. Zavěsil úlomek kovu na siloměr a zjistil, že ukazuje výchylku 0,91 N. Pak ponořil úlomek do vody. Siloměr ukázal 0,83 N. O jaký kov se jednalo?
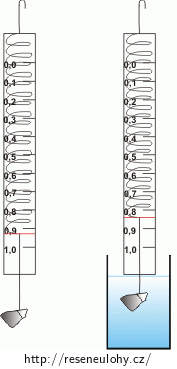
Nápověda 1
Jaká fyzikální veličina, kterou můžeme určit ze zadání, by nám pomohla zjistit, o jaký kov se jedná?
Nápověda 2
Rozmyslete si, jaké síly působí na úlomek zavěšený na siloměru ve vzduchu a ve vodě a co pro ně platí.
Nápověda 3
Vydělte rovnice (1), (2) a vyjádřete hustotu ρ.
Nápověda 4
Z tabulek či internetu zjistěte hustotu vody a vzduchu, dosaďte do vztahu (3) a číselně dopočítejte hustotu ρ. S pomocí tabulek či internetu určete, o jaký kov se jednalo.
Celkové řešení
Hledáme hustotu ρ kovu, ze kterého je úlomek.
Síly působící na úlomek ve vzduchu a ve vodě
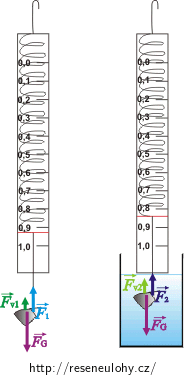
Ve vzduchu
Platí:
\[F_\mathrm{G}=F_{1}+F_\mathrm{v1}\,,\]kde FG je tíhová síla, F1 síla, kterou táhne siloměr, a Fv1 je vztlaková síla vzduchu.
Tedy:
\[mg=F_{1}+ V\rho_\mathrm{v} g\,,\]kde m je hmotnost úlomku, g tíhové zrychlení, V objem úlomku a ρv je hustota vzduchu.
Protože \(m=\rho V\), kde ρ je hustota úlomku, dostáváme:
\[\rho Vg=F_{1}+ V\rho_\mathrm{v} g\,.\]Vyjádříme F1:
\[F_{1}=Vg(\rho-\rho_\mathrm{v})\,.\tag{1}\]Ve vodě
Platí:
\[F_\mathrm{G}=F_{2}+F_\mathrm{v2}\,,\]kde F2 je síla, kterou táhne siloměr, a Fv2 je vztlaková síla vody.
Tedy:
\[mg=F_{2}+ V\rho_\mathrm{H_{2}O} g\,,\]kde ρH2O je hustota vody.
Protože \(m=\rho V\), dostáváme:
\[\rho Vg=F_{2}+ V\rho_\mathrm{H_{2}O} g\,.\]Vyjádříme F2:
\[F_{2}=Vg(\rho-\rho_\mathrm{H_{2}O})\,.\tag{2}\]Vydělení rovnic (1), (2) a vyjádření ρ
Vydělením rovnic (1), (2) dostáváme:
\[ \frac{F_{1}}{F_{2}}=\frac{Vg(\rho -\rho_\mathrm{v} )}{Vg(\rho-\rho_\mathrm{H_{2}O})}\,.\]Vykrátíme Vg a obě strany rovnice vynásobíme F2(ρ−ρH2O):
\[ F_{1}(\rho-\rho_\mathrm{H_{2}O})=F_{2}(\rho -\rho_\mathrm{v} )\,.\]Roznásobíme závorky, členy s ρ převedeme na levou stranu a zbylé členy na pravou stranu rovnice:
\[ F_{1}\rho-F_{2}\rho=F_{1}\rho_\mathrm{H_{2}O} -F_{2}\rho_\mathrm{v}\,.\]Vytkneme ρ a obě strany rovnice vydělíme (F1−F2):
\[\rho= \frac{F_{1}\rho_\mathrm{H_{2}O}-F_{2}\rho_\mathrm{v}}{F_{1}-F_{2}}\,.\tag{3}\]Číselné řešení
Ze zadání víme, že F1 = 0,91 N a F2 = 0,83 N.
Hustota vzduchu při 20 °C je podle tabulek: \(\rho_\mathrm{v} \dot= 1{,}2\,\mathrm{\frac{kg}{m^3}}\).
Hustota vody při 20 °C je podle tabulek: \(\rho_\mathrm{H_{2}O} \dot= 998\,\mathrm{\frac{kg}{m^3}}\).
Po dosazení do (3) získáme:
\[\rho= \frac{0{,}91{\cdot}998-0{,}83{\cdot}1{,}2}{0{,}91-0{,}83}\,\mathrm{\frac{kg}{m^3}} \dot = \frac{907}{0{,}08}\,\mathrm{\frac{kg}{m^3}} \dot = 11{,}3{\cdot}10^3\,\mathrm{\frac{kg}{m^3}}\,.\]V tabulkách můžeme dohledat, že hodnota \(\rho=11{,}3\cdot{10}^3\,\mathrm{{\frac{kg}{m^3}}}\) odpovídá olovu.
Odpověď
Hustota nalezeného úlomku je rovna: \[\rho= \frac{m_\mathrm{v}\rho_\mathrm{H_{2}O}-m_\mathrm{{H_{2}O}}\rho_\mathrm{v}}{m_\mathrm{v}-m_\mathrm{{H_{2}O}}} \dot = 11\cdot{10}^3\,\mathrm{\frac{kg}{m^3}}\,.\]
Tato hodnota odpovídá hustotě olova. Nalezený úlomek byl asi olověný.




