Pohyb daný graficky III
Úloha číslo: 135
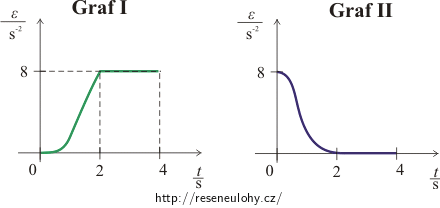
Kruhový kotouč se otáčí s úhlovým zrychlením ε, jehož závislost na čase je zadaná v grafech I a II. Bod A leží na okraji kotouče. Určete pro něj průběhy ε(t), ω(t), α(t) analyticky pro časový interval <0; 4s>.
V čase t = 0 s byl bod A v klidu a měl nulovou výchylku.
Graf I tvoří část paraboly a přímka, graf II sinusoida a přímka.
Poznámka: Parametrické rovnice by měly být zapsány ve tvaru např.:
\[y (t) \,=\, 1\,\mathrm{m}-2\,\mathrm{m\cdot s^{-1} }\cdot t.\]Pro zjednodušení zápisu jednotky ve vztazích nepíšeme.
Nápověda 1 pro graf č. I: Závislost ε(t)
Rozdělte si průběh ε(t) na dva intervaly.
Jaké funkce popisují na těchto intervalech průběh ε(t)?
Napište rovnice těchto funkcí. K tomu potřebujete alespoň dva body grafu, jejichž souřadnice znáte. Které to jsou?
Nápověda 2 pro graf č. I: Závislosti ω(t) a α(t)
Znáte závislost ε(t) úhlového zrychlení na čase. Jak odtud určíte závislost úhlové rychlosti na čase ω(t)? Postup je analogický jako u přímočarého pohybu.
Ze známé závislosti úhlové rychlosti na čase pak obdobným postupem určíte závislost úhlové výchylky na čase α(t) .
Nápověda 3 pro graf č. II: Závislost ε(t)
Postupujte podobně jako u grafu I. Rozdělte si průběh ε(t) na dva intervaly.
Jaké funkce popisují na těchto intervalech průběh ε(t)?
Napište rovnice těchto funkcí.
Nápověda 4 pro graf č. II: Závislosti ω(t) a α(t)
Znáte závislost ε(t) úhlového zrychlení na čase. Jak odtud určíte závislost úhlové rychlosti na čase ω(t)? Postup je analogický jako u přímočarého pohybu.
Ze známé závislosti úhlové rychlosti na čase pak obdobným postupem určíte závislost úhlové výchylky na čase α(t).
Postup je stejný jako u grafu I.
CELKOVÉ ŘEŠENÍ
Rozdělíme si v obou případech průběh \(\varepsilon(t) \) na dva intervaly,
interval <0 s; 2 s> a interval (2 s; 4 s>.
Graf č. I, interval <0 s; 2 s>:
Jedná se o graf funkce: \(\varepsilon (t) \,=\, at^{2}\)
(parabola procházející počátkem).
Bod [2; 8] leží na parabole, platí tedy:
\[8\,=\,a2^{2},\] \[a\,=\,2.\]Průběh funkce \(\varepsilon(t)\) je tedy: \(\varepsilon(t) \,=\, 2t^{2}.\)
Známe průběh funkce \(\varepsilon(t)\). Dále víme, že pro \(\omega(t)\) platí:
\[\omega(t)\,=\,\int{\varepsilon(t)}dt.\]Tedy:
\[\omega(t)\,=\, \int{2t^{2}}dt \,=\, 2\frac{t^{3}}{3}\,+\,C.\]Konstantu C určíme z počátečních podmínek:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \omega(0)\,=\,0,\] \[0\,=\,0\,+\,C,\] \[C\,=\,0,\]
\[\omega(t)\,=\,\frac{2}{3}t^3.\]Pro \(\alpha(t)\) platí:
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\,\int{\frac{2}{3}t^3}dt \,=\, \frac{2}{3}\,\frac{t^{4}}{4}\,+\,C.\]Konstantu C určíme z počátečních podmínek:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \alpha(0)\,=\,0,\] \[0\,=\,0\,+\,C,\] \[C\,=\,0,\]
\[\alpha(t)\,=\,\frac{t^{4}}{6}.\]Graf č. I, interval (2 s; 4 s>:
Průběh funkce \(\varepsilon(t)\) na tomto intervalu je: \(\varepsilon(t)\,=\,8.\)
Dále víme, že pro \(\omega(t)\) platí:
\[\omega(t)\,=\,\int{\varepsilon(t)}dt,\] \[\omega(t)\,=\,\int{8}dt\,=\, 8t\,+\,C.\]Známe průběh \(\omega(t)\) na intervalu <0 s; 2 s>, z něj dostáváme hodnotu \(\omega(2)\) v čase 2 s:
\[\omega(2)\,=\,\frac{2}{3}\cdot2^{3}\,=\,\frac{16}{3}.\]Pro konstantu C pak z počátečních podmínek platí:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \omega(2)\,=\,\frac{16}{3},\] \[\frac{16}{3}\,=\,8{\cdot}2\,+\,C,\] \[C\,=\,-\frac{32}{3},\]
\[\omega(t)\,=\,8t\,-\,\frac{32}{3}.\]Stejným způsobem pro \(\alpha(t)\):
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\, \int({8t\,-\,\frac{32}{3}})dt \,=\, 4t^{2}\,-\,\frac{32}{3}t\,+\,C.\]Známe průběh \(\alpha(t)\) na intervalu <0 s; 2 s>, z něj dostáváme hodnotu \(\alpha(2)\) v čase 2 s:
\[\alpha(2)\,=\,\frac{2^4}{6}\,=\,\frac{16}{6}\,=\,\frac{8}{3}.\]Pro konstantu C pak z počátečních podmínek platí:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \alpha(2)\,=\,\frac{8}{3},\] \[\frac{8}{3}\,=\,4{\cdot}2^{2}\,-\,\frac{32}{3}\cdot2\,+\,C,\] \[C\,=\,8,\]
\[\alpha(t)\,=\,4t^{2}\,-\,\frac{32}{3}t\,+\,8.\]II. Graf č. II, interval <0 s; 2 s>:
Postupujeme analogicky jako u grafu č. I.
Jedná se o graf funkce kosinus. Obecně je popsán rovnicí:
\[\varepsilon(t)\,=\,A\cos\frac{2\pi}{T}(t\,-\,C)\,+\,D,\]kde A je amplituda, T je perioda, C posunutí po vodorovné ose, D posunutí po svislé ose.
V našem konkrétním případě: A = 4 s−2, T = 4 s, C = 0, D = 4 s−2, a tedy:
\[\varepsilon(t)\,=\,=4\cos\frac{\pi}{2}t\,+\,4.\]Známe průběh funkce \(\varepsilon(t)\). Dále víme, že pro \(\omega(t)\) platí:
\[\omega(t)\,=\,\int{\varepsilon(t)}dt,\] \[\omega(t)\,=\, \int{(4\cos\frac{\pi}{2}t\,+\,4)}dt \,=\, \frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t\,+\,C.\]Konstantu C určíme z počátečních podmínek:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \omega(0)\,=\,0,\] \[0\,=\,\frac{8}{\pi}\sin0\,+\,0\,+\,C,\] \[C\,=\,0,\]
\[\omega(t)\,=\,\frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t.\]Pro \(\alpha(t)\) platí:
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\,\int{(\frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t)}dt \,=\, -\frac{16}{\pi^{2} }\cos\frac{\pi}{2}t\,+\,2t^{2}\,+\,C.\]Konstantu C určíme z počátečních podmínek:
\[t\,=\,0\,\mathrm{s}, \hspace{20px} \alpha(0)\,=\,0,\] \[0\,=\,-\frac{16}{\pi^{2} }\cos0\,+\,0\,+\,C,\] \[C\,=\,\frac{16}{\pi^{2} },\]
\[\alpha(t)\,=\,-\frac{16}{\pi^{2} }\cos\frac{\pi}{2}t\,+\,2t^{2}\,+\,\frac{16}{\pi^{2} }.\]Graf č. II, interval (2 s; 4 s>:
Známe průběh funkce \(\varepsilon(t)\) na tomto intervalu: \(\varepsilon(t)\,=\,0.\)
Dále víme, že pro \(\omega(t)\) platí:
\[\omega(t)\,=\,\int{\varepsilon(t)}dt,\] \[\omega(t) \,=\,\int{0}dt \,=\, C.\]Známe průběh \(\omega(t)\) na intervalu <0 s; 2 s>, z něj dostáváme hodnotu \(\omega(2)\) v čase 2 s:
\[\omega(2)\,=\,\frac{8}{\pi}\sin\frac{\pi}{2}2\,+\,4 {\cdot} 2\,=\,8.\]Pro konstantu C pak z počátečních podmínek platí:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \omega(2)\,=\, 8,\] \[C\,=\,8,\]
\[\omega(t)\,=\,8.\]Pro \(\alpha(t)\) platí:
\[\alpha(t)\,=\,\int{\omega(t)}dt,\] \[\alpha(t)\,=\,\int{8}dt\,=\,8t\,+\,C.\]Známe průběh \(\alpha(t)\) na intervalu <0 s; 2 s>, z něj dostáváme hodnotu \(\alpha(2)\) v čase 2 s:
\[\alpha(2)\,=\,-\frac{16}{\pi^{2}}\cos\frac{\pi}{2}2\,+\,2{\cdot} 2^{2}\,+\,\frac{16}{\pi^{2}}\,=\,\frac{32}{\pi^{2}}\,+\,8.\]Pro konstantu C pak z počátečních podmínek platí:
\[t\,=\,2\,\mathrm{s}, \hspace{20px} \alpha(2)\,=\,\frac{32}{\pi^{2}}\,+\,8,\] \[\frac{32}{\pi^{2}}\,+\,8\,=\,8 {\cdot} 2\,+\,C\,=\,16\,+\,C,\] \[C\,=\,\frac{32}{\pi^{2}}-8,\]
\[\alpha(t)\,=\,8t\,+\,\frac{32}{\pi^{2}}-8.\]Odpověď
Graf č. I, interval <0 s; 2 s>:
\[\varepsilon\,=\,2t^{2},\] \[\omega(t)\,=\,\frac{2}{3}t^3,\] \[\alpha(t)\,=\,\frac{t^{4}}{6}.\]Graf č. I, interval (2 s; 4 s>:
\[\varepsilon(t)\,=\,8,\] \[\omega(t)\,=\,8t\,-\,\frac{32}{3},\] \[\alpha(t)\,=\,4t^{2}\,-\,\frac{32}{3}t\,+\,8.\]Graf č. II, interval <0 s; 2 s>:
\[\varepsilon(t)\,=\,4\cos\frac{\pi}{2}t\,+\,4,\] \[\omega(t)\,=\,\frac{8}{\pi}\sin\frac{\pi}{2}t\,+\,4t,\] \[\alpha(t)\,=\,-\frac{16}{\pi^{2} }\cos\frac{\pi}{2}t\,+\,2t^{2}\,+\,\frac{16}{\pi^{2} }.\]Graf č. II, interval (2 s; 4 s>:
\[\varepsilon(t)\,=\,0,\] \[\omega(t)\,=\,8,\] \[\alpha(t)\,=\,8t\,+\,\frac{32}{\pi^{2}}-8.\]