Moment setrvačnosti obruče a disku

Úloha číslo: 556

Máme tenký disk a tenkou obruč.

A) Bez výpočtu odhadněte, zda bude mít při stejném poloměru, hmotnosti a poloze osy rotace větší moment setrvačnosti obruč nebo disk.

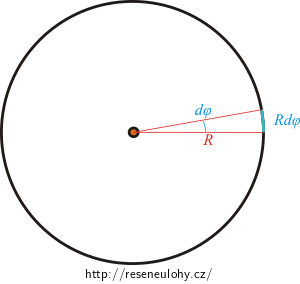
B) Určete moment setrvačnosti tenké obruče tvaru kružnice o poloměru R a hmotnosti m vzhledem k ose, která prochází kolmo jejím středem.

C) Určete moment setrvačnosti tenkého kruhového disku o poloměru R a hmotnosti m vzhledem k ose procházející kolmo jeho středem.

Nápověda A
Uvědomte si, na jakých veličinách a v kolikátých mocninách moment setrvačnosti tělesa závisí.
Řešení nápovědy A
Moment setrvačnosti závisí na rozložení hmoty vzhledem k ose rotace. Roste se čtvercem vzdálenosti od osy. Pokud tedy má disk a obruč stejnou hmotnost, pak má obruč větší moment setrvačnosti, protože celá její hmota je soustředěna na obvodu (není „plná“).
Nápověda 1B
Projděte si teorii vysvětlenou u příkladu Moment setrvačnosti tyče. Jak ji použijeme v tomto případě?
Řešení nápovědy 1B
Úlohu vyřešíme nejprve jednoduchou úvahou. Představme si, že obruč nasekáme na malé kousky délky ds a hmotnosti dm. Všechny tyto „kousky“ jsou stejně vzdálené od osy otáčení (vzdálenost R) a moment setrvačnosti každého z nich je roven:
\[ dJ_\mathrm{o} = dmR^2\,\]
(podle vztahu pro moment setrvačnosti hmotného bodu). Celkový moment setrvačnosti obruče pak dostaneme posčítáním momentů setrvačnosti všech kousků. Výsledek tedy bude:
\[J_\mathrm{o} = dm_1R^2 + dm_2R^2 + dm_3R^2 + ... =R^2(dm_1 + dm_2 + dm_3 + ...) = mR^2\,.\]
Tento výsledek ještě můžeme ověřit výpočtem.

Tenkou kružnicovou obruč můžeme uvažovat jako objekt charakterizovaný pouze svou délkou. Základní vztah využívající objemový integrál si upravíme:

\(J = \int_{V} \rho R^2 dV\)→ \(J_\mathrm{o} = \int \lambda R^2 ds,\)

přičemž meze integrálu budou tvořit počáteční a koncový bod křivky, λ je délková hustota a ds délka infinitezimálně malého kousku křivky.
Nápověda 2B
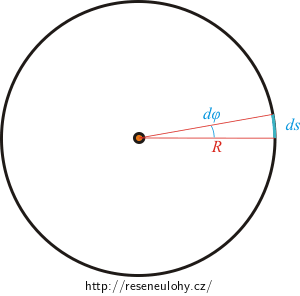
Rozmyslete si, jak bude vypadat konkrétní integrál. Jak vyjádříme délku malého kousku křivky ds, když známe poloměr kružnice a budeme uvažovat její část odpovídající nekonečně malému úhlu dφ? Neusnadní nám tento pohled určení mezí integrálu?
Řešení nápovědy 2B
Budeme-li úhel určovat v obloukové míře (tzn. v radiánech), pak pro jeho velikost platí:
\[\varphi = \frac{s}{R}\,,\]
kde s je délka vytnutého kružnicového oblouku a r poloměr kružnice.

Odtud pro nekonečně malý oblouček zjevně platí:
\[ds = Rd\varphi\,. \]

Budeme tedy integrovat přes úhel. Vzhledem k tomu, že má obruč tvar kružnice, budou integrální meze 0 a 2π (tj. integrál po celé délce kružnice).
\[J_\mathrm{o} = \int \lambda R^2 ds\,,\] \[J_\mathrm{o} = \int^{2\pi}_{0} \lambda R^2 Rd\varphi\,,\] \[J_\mathrm{o} = \int^{2\pi}_{0} \lambda R^3 d\varphi = \lambda R^3\left[\varphi\right]_{0}^{2\pi} = \lambda R^3 2\pi\,.\]
Připomeneme si vztahy pro délkovou hustotu pro případ kružnice:
\[\lambda = \frac{m}{o} = \frac{m}{2\pi R}\,,\] \[m = 2\pi\lambda R\,.\]
A odtud:
\[J_\mathrm{o} = mR^2\,.\]
Nápověda 1C
Jak se bude lišit výpočet momentu setrvačnosti disku a obruče? Nepomohou nám nějak výsledky předchozí části?
Řešení nápovědy 1C
Na disk by se šlo dívat jako na těleso vzniklé spojením nekonečného množství tenkých „obrouček“ postupně vyplňujících celý poloměr.

Zkuste v duchu těchto přiblížení pozměnit úvahu z předcházející části.
Nápověda 2C
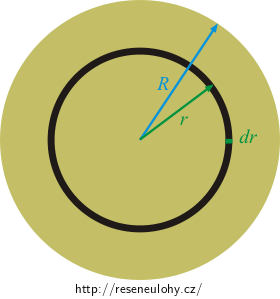
Vyjádřete moment setrvačnosti jedné „obroučky“. Využijte přitom výsledek z předchozí části.

Celkový moment setrvačnosti disku pak spočítáte sečtením příspěvků od všech „obrouček“ – neboli integrací.
Řešení nápovědy nápovědy 2C
Moment setrvačnosti jedné „obroučky“ je:
\[dJ_\mathrm{d} = dmr^2\,.\]
Kde r je poloměr a dm hmotnost „obroučky“:
\[dm = \sigma 2\pi r dr\,.\]
σ je plošná hustota, pro kterou v případě disku platí:
\[\sigma = \frac{m}{S} = \frac{m}{\pi R^2}\,.\]
Pak:
\[dJ_\mathrm{d} = 2\pi \sigma r^3 dr\,.\]
Celkový moment setrvačnosti disku získáme posčítáním momentů setrvačnosti všech obrouček:
\[J_\mathrm{d} = \int dJ_\mathrm{d} = \int_{0}^{R} 2\pi \sigma r^3 dr = 2\pi \sigma \left[\frac{r^4}{4}\right]_{0}^{R} = \frac{1}{2}\pi \sigma R^4\,.\]
Dosadíme za plošnou hustotu:
\[J_\mathrm{d} = \frac{1}{2}\pi\frac{m}{\pi R^2}R^4 = \frac{1}{2} mR^2\,.\]
Další možné řešení C
Úlohu lze také velmi jednoduše řešit převedením na dvojný integrál v polárních souřadnicích:
\[J_\mathrm{d} = \int_{S} \sigma r^2 dS\,.\]

\[dS = rd \varphi dr\,,\] \[J_\mathrm{d} = \int_{0}^{2\pi} \int_{0}^{R} \sigma r^3 dr d \varphi = \frac{1}{2}\pi \sigma R^4 = \frac{1}{2}m R^2\,.\]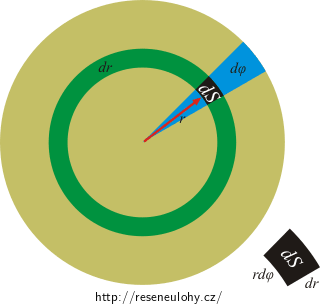
Odpověď
I bez výpočtu lze určit, že moment setrvačnosti obruče bude díky rozložení hmoty vzhledem k ose rotace větší než moment setrvačnosti disku.

Moment setrvačnosti tenké obruče o hmotnosti m a poloměru R vzhledem k ose procházející jejím středem je:
\[J_\mathrm{o} = mR^2\,.\]
Moment setrvačnosti disku o hmotnosti m a poloměru R vzhledem k ose procházející jeho středem je:
\[J_\mathrm{d} = \frac{1}{2} mR^2\,.\]