Snášení letadla
Úloha číslo: 211
Letadlo letí stálou rychlostí v přímo na sever. Náhle ze západu začne foukat vítr, jehož rychlost se rovnoměrně zvyšuje z počáteční hodnoty 0 m·s-1 na konečnou hodnotu 10 m·s-1, které dosáhne za 1 h. O jakou vzdálenost směrem na východ bude letadlo sneseno během této hodiny, pokud pilot neopraví kurz?
Zápis
w1 = 0 m·s-1 počáteční rychlost větru w2 = 10 m·s-1 konečná rychlost větru T = 1 h doba unášení s = ? (m) vzdálenost, o kterou bude letadlo uneseno na východ Nápověda 1 - druh pohybu
Předpokládejme, že letadlo je v každém okamžiku unášeno takovou rychlostí, jakou právě vane vítr. Jaký druh pohybu z hlediska rychlosti letadlo ve směru ze západu na východ vykonává? Závisí tento pohyb nějak na rychlosti letadla v?
Nápověda 2 - dráha pohybu
Jak lze určit dráhu tohoto pohybu?
Nápověda 3 - vztah pro zrychlení
Ve vztahu (1) známe čas (t = T), zbývá určit zrychlení a. Vzpomenete si, jak je definováno?
Nápověda 4
Zkombinujte vztahy (1) a (2) a vypočítejte dráhu uraženou ve směru ze západu na východ.
Celkové řešení
Ve směru ze západu na východ rychlost větru (a tedy i letadla) rovnoměrně roste – jde tedy o rovnoměrně zrychlený pohyb.
Dráha s rovnoměrně zrychleného pohybu je dána vztahem:
\[s\,=\,\frac{1}{2}at^2\,,\tag{1}\]
kde a je zrychlení a t = T doba zrychleného pohybu.
Zrychlení a definujeme jako:
\[a\,=\,\frac{{\Delta}v}{{\Delta}t}\,,\tag{2}\]
kde Δv je změna rychlosti za čas Δt.
Vyjádření zrychlení ze vztahu (2) dosadíme do rovnice (1):
\[s\,=\,\frac{1}{2}aT^2\,=\,\frac{1}{2}\frac{{\Delta}v}{{\Delta}t}T^2.\]V našem případě je zjevně doba zrychlování Δt = T = 1 h a změna rychlosti Δv = w2 − w1. Tedy:
\[s\,=\,\frac{1}{2}\frac{w_2\,-\,w_1}{t}T^2\,=\,\frac{1}{2}(w_2\,-\,w_1)T\,.\]Číselně:
\[w_1\,=\,0\,\mathrm{m{\cdot}s^{-1}},\] \[w_2\,=\,10\,\mathrm{m{\cdot}s^{-1}},\] \[T\,=\,1\,\mathrm{h}\,=\,3600\,\mathrm{s},\]\[s\,=\,\frac{1}{2}(w_2\,-\,w_1)T\,=\,(\frac{1}{2}{\cdot}(10\,-\,0){\cdot}3600)\,\mathrm{m}\,=\,18000\,\mathrm{m}\,=\,18\,\mathrm{km}.\]
Letadlo bude ve směru na východ sneseno o 18 km.
Alternativní řešení 1
Úlohu lze řešit také pomocí grafu závislosti rychlosti w na čase t. Pro rovnoměrně zrychlený pohyb je grafem této závislosti přímka určená v našem případě body A, B. Jejich souřadnice ze zadání známe:
\[A\,=\,[t_1\,=\,0\,\mathrm{s};\,w_1\,=\,0\,\mathrm{m{\cdot}s^{-1}}],\] \[B\,=\,[t_2\,=\,3600\,\mathrm{s};\,w_2\,=\,10\,\mathrm{m{\cdot}s^{-1}}].\]Vyneseme body A, B do grafu a spojíme je. Hledaná dráha je rovna obsahu plochy pod grafem, tedy pod úsečkou AB. Úloha se tak redukuje na výpočet obsahu pravoúhlého trojúhelníka, který má strany Δw = 10 m·s−1 a Δt = 3600 s.
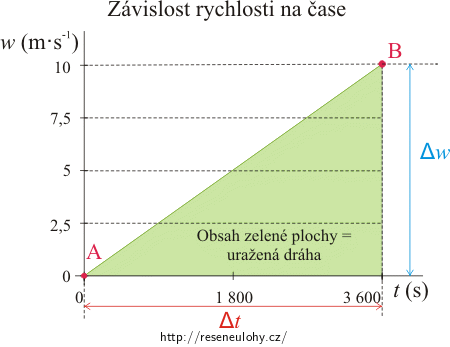
Zjevně platí:
\[s\,=\,\frac{1}{2}{\Delta}w{\Delta}t\,=\,(\frac{1}{2}{\cdot}10{\cdot}3600)\,\mathrm{m}\,=\,18000\,\mathrm{m}\,=\,18\,\mathrm{km}.\]Alternativní řešení 2
Pro milovníky integrování nabízíme ještě jeden způsob. Podobně jako v Alternativním řešení 1 sestrojíme závislost rychlosti na čase a vyjádříme předpis této přímé úměrnosti:
\[w(t)\,=\,k{\cdot}t\,,\] kde k je směrnice přímky, jež je grafem. Číselnou hodnotu směrnice vypočítáme jako: \[\{k\}\,=\,\frac{\{{\Delta}w\}}{\{{\Delta}t\}}\,=\,\frac{10}{3600}\,=\,\frac{1}{360}\,.\]Tedy:
\[\{w(t)\}\,=\,\frac{1}{360}{\cdot}\{t\}\,.\]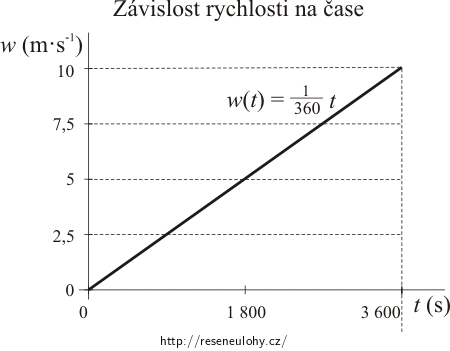
Pro získání dráhy nyní zintegrujeme vztah pro rychlost v mezích 0 s až 3600 s:
\[s\,=\int_0^{T} w(t)dt\,=\int_0^{T} k{\cdot}t dt\,=\, k\left[\frac{t^2}{2}\right]_{0}^{T}\,=\,\frac{1}{2}{\cdot} k{\cdot}T^2\,.\]
Číselně:
\[s \,=\,\frac{1}{2}{\cdot}\frac{1}{360}{\cdot}3600^2\,\mathrm{m} \,=\,18000\,\mathrm{m}\,=\,18\,\mathrm{km}\,.\]
Výsledek
\[s\,=\,\frac{1}{2}(w_2\,-\,w_1)T\,=\,18\,\mathrm{km}\]
Pokud pilot neopraví kurz, bude letadlo sneseno za 1 hodinu o 18 km na východ.




