Kulička plovoucí ve rtuti
Úloha číslo: 793
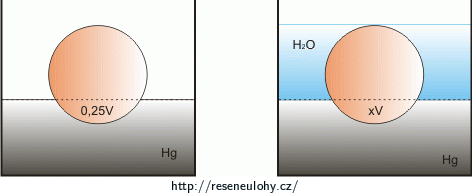
Homogenní kulička plave ve rtuti tak, že je v ní ponořena čtvrtina jejího objemu. Na rtuť nalijeme vodu tak, aby byla ponořená celá kulička. Jaká část objemu kuličky bude v tomto případě ponořená ve rtuti?
Na základě úvahy nejprve řekněte, zda bude menší či větší než v předchozím případě, a pak to spočítejte.
Nápověda 1
Jaké síly působí na kuličku v obou případech? Nakreslete je do obrázku.
Nápověda 2
Kulička je v obou případech v rovnováze. Co v této situaci platí pro působící síly?
Nápověda 3
Jak vypočítáme velikost tíhové síly působící na kuličku, vztlakové síly rtuti a vztlakové síly vody?
Nápověda 4
Víme, jaké síly působí na kuličku a jak vypočítáme jejich velikosti. Dosaďte do vztahů (1) a (2) za velikosti sil a vyjádřete hledaný objem.
Nápověda 5
Našli jsme \(x\), pro které platí:
\(x=\frac{\frac{1}{4}\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}}{\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}}. \)
V tabulkách dohledejte potřebné hodnoty a číselně dopočítejte \(x\).
Celkové řešení
Nakreslíme si síly působící na kuličku.
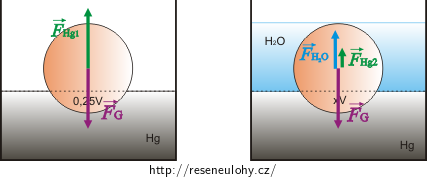
V prvním případě působí na kuličku tíhová síla a vztlaková síla rtuti. Ve druhém případě na ni navíc působí vztlaková síla vody.
Pro tíhovou sílu \(F_\mathrm{G}\) v obou případech platí vztah:
\[F_\mathrm{G}=mg\,,\tag{1}\]kde \(m\) je hmotnost kuličky a \(g\) je tíhové zrychlení.
Obecně pro vztlakovou sílu \(F_\mathrm{vz}\) platí vztah:
\[F_\mathrm{vz}=V_\mathrm{pct}\rho_\mathrm{kap}g\,,\]
kde \(V_\mathrm{pct}\) je objem ponořené části tělesa a \(\rho_\mathrm{kap}\) je hustota kapaliny.
Pro vztlakovou sílu rtuti v prvním případě \(F_\mathrm{Hg_{1}}\) bude \(V_\mathrm{pct}=\frac{1}{4}V\) a \(\rho_\mathrm{kap}=\rho_\mathrm{Hg}\), kde \(V\) je objem kuličky a \(\rho_\mathrm{Hg}\) je hustota rtuti. Tedy platí vztah:
\[F_\mathrm{Hg_{1}}=\frac{1}{4}V\rho_\mathrm{Hg}g\,.\tag{2}\]
Pro vztlakovou sílu rtuti ve druhém případě \(F_\mathrm{Hg_{2}}\) bude \(V_\mathrm{pct}=xV\) a \(\rho_\mathrm{kap}=\rho_\mathrm{Hg}\), kde \(x\) je část jejího objemu, která je ponořená ve rtuti. Tedy platí vztah:
\[F_\mathrm{Hg_{2}}=xV\rho_\mathrm{Hg}g\,.\tag{3}\]
Pro vztlakovou sílu vody \(F_\mathrm{H_{2}O}\) bude \(V_\mathrm{pct}=V-xV\) a \(\rho_{kap}=\rho_\mathrm{H_{2}O}\), kde \(\rho_\mathrm{H_{2}O}\) je hustota vody. Tedy platí vztah:
\[F_\mathrm{H_{2}O}=(V-xV)\rho_\mathrm{H_{2}O}g\,.\tag{4}\]
Kulička je v obou případech v rovnováze, proto je výsledná síla působící na kuličku nulová. Z toho důvodu se v prvním případě velikost tíhové síly působící na kuličku musí rovnat velikosti vztlakové síly rtuti. Podobně ve druhém případě se velikost tíhové síly působící na kuličku musí rovnat součtu velikostí vztlakových sil rtuti a vody.
V prvním případě se velikost tíhové síly působící na kuličku rovná velikosti vztlakové síly rtuti:
\[F_\mathrm{G}=F_\mathrm{Hg_{1}}.\]
Podle (1) a (2) dostáváme:
\[mg=\frac{1}{4}V\rho_\mathrm{Hg}g\,.\]
\(g\) vykrátíme a \(m\) rozepíšeme dle vztahu \(m=\rho_\mathrm{k}V\), kde \(\rho_\mathrm{k}\) je hustota kuličky:
\[\rho_\mathrm{k}V=\frac{1}{4}V\rho_\mathrm{Hg}.\]
\(V\) vykrátíme a dostaneme:
\[\rho_\mathrm{k}=\frac{1}{4}\rho_\mathrm{Hg}.\tag{5}\]
Ve druhém případě se velikost tíhové síly působící na kuličku rovná součtu velikostí vztlakových sil rtuti a vody:
\[F_\mathrm{G}=F_\mathrm{Hg_{2}}+F_\mathrm{H_{2}O}.\]
Dle (1), (3) a (4) dostáváme:
\[mg=xV\rho_\mathrm{Hg}g+(V-xV)\rho_\mathrm{H_{2}O}g.\]
\(g\) vykrátíme, \(m\) rozepíšeme dle vztahu \(m=\rho_\mathrm{k}V\) a ze závorky vytkneme \(V\):
\[\rho_\mathrm{k}V=xV\rho_\mathrm{Hg}+V(1-x)\rho_\mathrm{H_{2}O}.\]
\(V\) vykrátíme a dle (5) rozepíšeme \(\rho_\mathrm{k}\):
\[\frac{1}{4}\rho_\mathrm{Hg}=x\rho_\mathrm{Hg}+(1-x)\rho_\mathrm{H_{2}O}.\]
Roznásobíme závorku a vytkneme x:
\[\frac{1}{4}\rho_\mathrm{Hg}=x(\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O})+\rho_\mathrm{H_{2}O}.\]
Obě strany rovnice upravíme tak, že od nich odečteme \(\rho_\mathrm{H_{2}O}\) a vydělíme je výrazem \(\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}\). Tím získáme \(x\):
\[x=\frac{\frac{1}{4}\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}}{\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}}. \]
Číselné řešení
V tabulkách dohledáme následující dvě hodnoty:
\[\rho_\mathrm{Hg}=13 600 \mathrm{\frac{kg}{m^3}}\,,\]
\[\rho_\mathrm{H_{2}O}= 1 000 \mathrm{\frac{kg}{m^3}}\,,\]
které dosadíme do vztahu pro \(x\):
\[x=\frac{\frac{1}{4}{\cdot}13600-1000}{13600-1000} \dot= 0{,}19\,.\]
Odpověď
Ve druhém případě je ve rtuti ponořena část objemu \(x=\frac{\frac{1}{4}\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}}{\rho_\mathrm{Hg}-\rho_\mathrm{H_{2}O}} \dot=0{,}19\), což je 19 % objemu kuličky.





