Kosmická sonda
Úloha číslo: 145
Kosmická sonda pohybující se rychlostí o velikosti v0 za letu exploduje a rozpadne se na 3 části o stejné hmotnosti. Jedna část pokračuje v letu původním směrem, zbývající dvě v různých směrech, které svírají s původním směrem úhel 60° a −60°. Energie vyvinutá při explozi je dvakrát tak velká jako kinetická energie, kterou měla sonda bezprostředně před explozí. Určete velikost rychlosti a kinetickou energii jednotlivých částí bezprostředně po explozi.
Zápis
m hmotnost sondy m/3 hmotnost jednotlivých částí sondy v0 velikost rychlosti sondy před explozí α = 60° úhel vychýlení 1. a 3. části sondy v1 = ? velikost rychlosti 1. části sondy těsně po explozi v2 = ? velikost rychlosti 2. části sondy těsně po explozi v3 = ? velikost rychlosti 3. části sondy těsně po explozi Ek1 = ? kinetická energie 1. části sondy těsně po explozi Ek2 = ? kinetická energie 2. části sondy těsně po explozi Ek3 = ? kinetická energie 3. části sondy těsně po explozi Rozbor
Při řešení úlohy využijeme zákon zachování hybnosti (ZZH) a energie (ZZE).
Nápověda 1 - ZZH
Nakreslete si obrázek a zvolte vhodně soustavu souřadnic. Rozepište si zákon zachování hybnosti pro naši situaci.
Nápověda 2 - ZZE
Napište si zákon zachování energie pro naši konkrétní situaci. Uvědomte si, jaká je celková energie sondy při explozi a jaká bezprostředně po jejím rozpadu. Vyjádřete vztahy pro rychlosti jednotlivých části.
Nápověda 3 - kinetická energie části sondy
Vyjádřete si vztahy pro kinetickou energii jednotlivých částí sondy a dosaďte za příslušné rychlosti.
Celkové řešení
Při řešení úlohy využijeme zákon zachování hybnosti (ZZH) a energie (ZZE).
Nakreslíme obrázek situace:
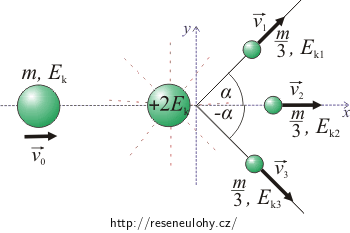
\(m\)…hmotnost sondy,
\(v_0\)…rychlost sondy před explozí,
\(v_1\)…rychlost 1. části sondy těsně po explozi,
\(v_2\)…rychlost 2. části sondy těsně po explozi,
\(v_3\)…rychlost 3. části sondy těsně po explozi,
\(\alpha\)…úhel vychýlení 1. a 3. části sondy.
Soustavu souřadnic volíme tak, že osa x má směr pohybu sondy před explozí a osa y je na ni kolmá.
ZZH: Celková hybnost soustavy se zachovává.
\[\vec{p}\,=\,\vec{p_1}+\vec{p_2}+\vec{p_3}\]\(\vec{p}\)…vektor hybnosti sondy před explozí
\(\vec{p_1}\)…vektor hybnosti 1. části sondy těsně po explozi
\(\vec{p_2}\)…vektor hybnosti 2. části sondy těsně po explozi
\(\vec{p_3}\)…vektor hybnosti 3. části sondy těsně po explozi
\[m\vec{v_0}\,=\,\frac{m}{3}\vec{v_1}+\frac{m}{3}\vec{v_2}+\frac{m}{3}\vec{v_3}\]Skalárně:
x-ová složka:
\[mv_0\,=\,\frac{1}{3}mv_1\cos\alpha + \frac{1}{3}mv_2 + \frac{1}{3}mv_3\cos\left(-\alpha\right),\] \[cos\left(-\alpha\right)\,=\, cos\alpha,\] \[mv_0\,=\,\frac{1}{3}mv_1\cos\alpha + \frac{1}{3}mv_2 + \frac{1}{3}mv_3\cos\alpha.\tag{1}\]y-ová složka:
\[0\,=\,\frac{1}{3}mv_1\sin\alpha + \frac{1}{3}mv_3\sin\left(-\alpha\right),\] \[sin\left(-\alpha\right)\,=\, - sin\alpha,\] \[0\,=\,\frac{1}{3}mv_1\sin\alpha - \frac{1}{3}mv_3\sin\alpha.\tag{2}\]Ze vztahu (2) vyjádříme rychlost 1. části sondy \(v_1\):
\[v_1\sin\alpha\,=\,v_3\sin\alpha,\] \[v_1\,=\,v_3.\tag{3}\]Dosadíme do vztahu (1):
\[mv_0\,=\,2\frac{1}{3}mv_1\cos\alpha + \frac{1}{3}mv_2.\]Odtud vyjádříme rychlost 2. části sondy těsně po srážce:
\[v_2\,=\,3v_0-2v_1\cos\alpha.\tag{4}\]ZZE: Součet kinetické energie sondy před explozí a energie vyvinuté při explozi je roven součtu kinetické energie jednotlivých části sondy po explozi:
\[\mathrm{ZZE:} \hspace{15px} E_\mathrm{k}+ 2E_\mathrm{k}\,=\,E_\mathrm{k1}+E_\mathrm{k2}+E_\mathrm{k3}\]\(E_\mathrm{k}\)…počáteční kinetická energie sondy
\(2E_\mathrm{k}\)…energie vyvinutá při explozi
\(E_\mathrm{k1}\)…kinetická energie 1. části sondy těsně po explozi
\(E_\mathrm{k2}\)…kinetická energie 2. části sondy těsně po explozi
\(E_\mathrm{k3}\)…kinetická energie 3. části sondy těsně po explozi
\[\frac{1}{2}mv_0^2+2\frac{1}{2}mv_0^2\,=\,\frac{1}{2}\frac{m}{3}v_1^2+\frac{1}{2}\frac{m}{3}v_2^2+\frac{1}{2}\frac{m}{3}v_3^2\] \[\frac{3}{2}mv_0^2\,=\,\frac{1}{6}mv_1^2+\frac{1}{6}mv_2^2+\frac{1}{6}mv_3^2.\]Rovnici vydělíme hmotností m a vynásobíme šesti:
\[9v_0^2\,=\,v_1^2+v_2^2+v_3^2.\]Za rychlost v3 dosadíme ze vztahu (3):
\[9v_0^2=2v_1^2+v_2^2.\]Za rychlost v2 dosadíme ze vztahu (4):
\[9v_0^2=\,2v_1^2+\left(3v_0-2v_1\cos\alpha\right)^2=\,2v_1^2+9v_0^2-12v_0v_1\cos \alpha +4v_1^2\cos ^2\alpha.\]
Rovnici upravíme a vyjádříme rychlost v1:
\[2v_1^2\left(1+2\cos^2 \alpha\right) \,=\, 12v_0v_1\cos \alpha,\] \[v_1\left(1+2\cos^2 \alpha\right) \,=\, 6v_0\cos \alpha,\] \[v_1\,=\,v_3\,=\,\frac{6v_0\cos \alpha}{1+2\cos^2 \alpha},\] \[\cos \alpha\,=\,\cos 60^{\circ}\,=\,\frac{1}{2},\] \[v_1\,=\,v_3\,=\,\frac{3v_0}{1+\frac{1}{2}}\,=\,2v_0.\]Dosazením do vztahu (4) získáme rychlost v2:
\[v_2\,=\,3v_0-\frac{12v_0\cos^2 \alpha}{1+2\cos^2 \alpha}\,=\,\frac{3v_0\left(1+2\cos^2 \alpha -4\cos^2 \alpha\right)}{1+2\cos^2 \alpha}\,=\,\frac{3v_0\left(1-2\cos^2 \alpha\right)}{1+2\cos^2 \alpha},\]
\[\cos \alpha\,=\,\cos 60^{\circ}\,=\,\frac{1}{2},\] \[v_2\,=\,\frac{3v_0\left(1-\frac{1}{2}\right)}{1+\frac{1}{2}}\,=\,v_0.\]Vyjádříme kinetickou energii jednotlivých částí sondy a dosadíme za příslušné rychlosti.
Kinetická energie 1. a 3. části sondy:
\[E_\mathrm{k1}\,=\,E_\mathrm{k3}\,=\,\frac{1}{6}mv_1^2,\] \[E_\mathrm{k1}\,=\,\frac{1}{6}m\frac{36v_0^2\cos^2\alpha}{\left(1+2\cos^2\alpha\right)^2}\,=\,6mv_0^2\frac{\cos^2\alpha}{\left(1+2\cos^2\alpha\right)^2},\] \[\cos \alpha\,=\,\cos 60^{\circ}\,=\,\frac{1}{2},\] \[E_\mathrm{k1}\,=\,6mv_0^2\frac{\frac{1}{4}}{\left(1+\frac{1}{2}\right)^2}\,=\,\frac{6}{9}mv_0^2,\] \[E_\mathrm{k1}\,=\,E_\mathrm{k3}\,=\,\frac{2}{3}mv_0^2\,=\,\frac{4}{3}E_\mathrm{k}.\]Kinetická energie 2. části sondy:
\[E_\mathrm{k2}\,=\,\frac{1}{6}mv_2^2,\] \[E_\mathrm{k2}\,=\,\frac{1}{6}m\frac{9v_0^2\left(1-2\cos^2\alpha\right)^2}{\left(1+2\cos^2\alpha\right)^2}\,=\,3\frac{mv_0^2}{2}\frac{\left(1-2\cos^2\alpha\right)^2}{\left(1+2\cos^2\alpha\right)^2},\] \[\cos \alpha\,=\,\cos 60^{\circ}\,=\,\frac{1}{2},\] \[E_\mathrm{k2}\,=\,3\frac{mv_0^2}{2}\frac{\left(1-\frac{1}{2}\right)^2}{\left(1+\frac{1}{2}\right)^2}\,=\,\frac{3}{2}mv_0^2\cdot\frac{4}{4{\cdot}9},\] \[E_\mathrm{k2}\,=\,\frac{mv_0^2}{6}\,=\,\frac{1}{3}E_\mathrm{k}.\]Odpověď:
Velikost rychlosti 1. a 3. části sondy bezprostředně po explozi je \[v_1\,=\,v_3\,=\,\frac{6v_0\cos\alpha}{1+2\cos^2\alpha}\,=\,2v_0.\]
Velikost rychlosti 2. části bezprostředně po explozi je \[v_2\,=\,\frac {3v_0\left(1-2\cos^2\alpha\right)}{1+2\cos^2\alpha}\,=\,v_0.\]
Kinetická energie 1. a 3. části sondy bezprostředně po explozi je \[E_\mathrm{k1}\,=\,E_\mathrm{k3}\,=\,6m\frac{v_0^2\cos^2\alpha}{\left(1+2\cos^2\alpha\right)^2}\,=\,\frac{2}{3}mv_0^2\,=\,\frac{4}{3}E_\mathrm{k}.\]
Kinetická energie 2. části sondy bezprostředně po explozi je \[E_\mathrm{k2}\,=\,\frac{3}{2}m\frac{v_0^2\left(1-\cos^2\alpha\right)^2}{\left(1+2\cos^2\alpha\right)^2}\,=\,\frac{mv_0^2}{6}\,=\,\frac{1}{3}E_\mathrm{k}.\]
Odpověď
Velikost rychlosti 1. a 3. části sondy bezprostředně po explozi je \[v_1\,=\,v_3\,=\,\frac{6v_0\cos\alpha}{1+2\cos^2\alpha}\,=\,2v_0.\]
Velikost rychlosti 2. části bezprostředně po explozi je \[v_2\,=\,\frac {3v_0\left(1-2\cos^2\alpha\right)}{1+2\cos^2\alpha}\,=\,v_0.\]
Kinetická energie 1. a 3. části sondy bezprostředně po explozi je \[E_\mathrm{k1}\,=\,E_\mathrm{k3}\,=\,6m\frac{v_0^2\cos^2\alpha}{\left(1+2\cos^2\alpha\right)^2}\,=\,\frac{2}{3}mv_0^2\,=\,\frac{4}{3}E_\mathrm{k}.\]
Kinetická energie 2. části sondy bezprostředně po explozi je \[E_\mathrm{k2}\,=\,\frac{3}{2}m\frac{v_0^2\left(1-\cos^2\alpha\right)^2}{\left(1+2\cos^2\alpha\right)^2}\,=\,\frac{mv_0^2}{6}\,=\,\frac{1}{3}E_\mathrm{k}.\]





