Kyvadlo na kolotoči
Úloha číslo: 481
Na kolotoči je ve vzdálenosti 2 metry od osy otáčení pověšeno půlkilogramové závaží na závěsu délky 1 metr, které je vychýleno o úhel velikosti 10° z rovnovážné polohy. Jaká je oběžná doba kolotoče?
Řešte z hlediska inerciálního systému i z hlediska neinerciální soustavy kolotoče.
Zápis
r = 2 m vzdálenost závěsu od osy kolotoče l = 1 m délka závěsu α = 10° odchylka závěsu od svislého směru m = 0,5 kg hmotnost závaží T = ? (s) oběžná doba kolotoče Z tabulek: g = 9,81 m·s−2 tíhové zrychlení Nápověda 1: Náčrtek z pohledu inerciálního a neinerciálního systému
Udělejte si dva náčrtky. Do jednoho zakreslete síly působící na závaží z pohledu inerciálního pozorovatele, který stojí vedle kolotoče.
Do druhého vyznačte síly působící na závaží z pohledu neinerciálního pozorovatele, který se otáčí spolu s kolotočem.
Rozmyslete si, jak se od sebe budou oba pohledy lišit a jak se vzhledem k jednotlivým pozorovatelům závaží pohybuje. Budou všechny síly vypadat v obou případech stejně? Bude jich stejný počet?
Nápověda 2: Pohybová rovnice z pohledu inerciálního pozorovatele
Shrňte do vektorové rovnice, co platí pro síly působící na závaží z pohledu inerciálního pozorovatele.
Zvolte souřadnou soustavu a přepište rovnici skalárně. Vyjádřete hledanou oběžnou dobu.
Nápověda 3: Pohybová rovnice z pohledu neinerciálního pozorovatele
Shrňte do vektorové rovnice, co platí pro síly působící na závaží z pohledu neinerciálního pozorovatele.
Čemu se musí rovnat součet všech sil, pokud je závaží vzhledem k pozorovateli v klidu?
Zvolte souřadnou soustavu a přepište rovnici skalárně. Vyjádřete hledanou oběžnou dobu.
Odpověď
Pro inerciální i neinerciální soustavu dostáváme:
\[ T = 2\pi \sqrt{\frac{r + l\sin\alpha}{g \tan{\alpha}}}.\]Oběžná doba kyvadla je 7 s.
Celkové řešení
a) Řešení z pohledu inerciálního pozorovatele stojícího vedle kolotoče
Z pohledu inerciálního pozorovatele stojícího vedle kolotoče vykonává závaží rovnoměrný pohyb po kružnici.
Jaké síly na závaží působí?
Závaží drží na kolotoči vlákno, jehož silové působení je vyjádřeno jeho tahem \(\vec{F}_\mathrm{T}\).
Samozřejmě působí tíhová síla \(\vec{F}_\mathrm{G}\).
Jejich složením dostáváme sílu \(\vec{F}_\mathrm{d}\), která směřuje do středu otáčení a zakřivuje pohyb závaží.
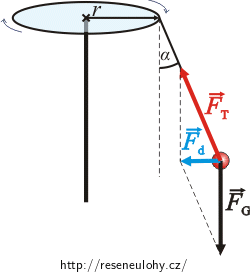
Pro výslednici sil platí:
\[\vec{F}_\mathrm{T} + \vec{F}_\mathrm{G} = \vec{F}_\mathrm{d} = m\vec{a}_\mathrm{n},\]kde \(\vec{F}_\mathrm{T}\) je tah provázku, \(\vec{F}_\mathrm{G}\) je tíhová síla, \(\vec{F}_\mathrm{d}\) je jejich výslednice a \(\vec{a}_\mathrm{n}\) dostředivé zrychlení.
Přepíšeme vektorovou rovnici skalárně do směru osy x a osy y (orientace viz obrázek):
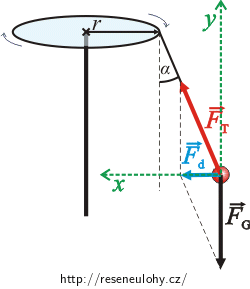
Vodorovný směr (osa x):
\[{F}_\mathrm{T} \mathrm{sin}\alpha= m{a}_\mathrm{n}.\]Kolmý směr (osa y):
\[{F}_\mathrm{T} \mathrm{cos}\alpha = mg.\]Vyjádříme-li z druhé rovnice FT a dosadíme-li do první, dostáváme:
\[mg \mathrm{tg}\alpha = m{a}_\mathrm{n},\] \[g \mathrm{tg}\alpha = {a}_\mathrm{n}.\]Pro pohyb po kružnici o poloměru ρ s využitím vztahů pro převod obvodové a úhlové rychlosti platí
\[{a}_\mathrm{n} = \frac{v^2}{\rho} = \omega^2\rho.\]Dosadíme:
\[g \mathrm{tg}\alpha = \omega^2\rho.\]Připomeňme si vztah mezi úhlovou rychlostí ω a periodou pohybu po kružnici T:
\[\omega = \frac{2\pi}{T}.\]Pak:
\[g \mathrm{tg}\alpha = \frac{4\pi^2}{T^2} \rho.\]Odtud:
\[ T^2 = 4\pi^2\frac{\rho}{g \mathrm{tg}{\alpha}},\] \[ T = 2\pi \sqrt{\frac{\rho}{g \mathrm{tg}{\alpha}}}.\]Poloměr kružnice ρ, po které závaží obíhá, je dán součtem vzdálenosti upevnění závěsu r od osy kolotoče a vzdálenosti rα vzniklé vykývnutím závaží délky l ze svislé klidové polohy o úhel α.
Platí tedy:
\[\rho = r+r_\alpha = r + l\sin\alpha.\]Odtud dostáváme výsledný vztah:
\[ T = 2\pi \sqrt{\frac{r + l\sin\alpha}{g \mathrm{tg}{\alpha}}}.\]Číselně:
\[ T = 2\pi \sqrt{\frac{2 + 1 \mathrm{sin}10^{\circ}}{9{,}81 \mathrm{tg}10^{\circ}}}\,\mathrm{s} = 7\,\mathrm{s}.\]b) Řešení z pohledu neinerciálního pozorovatele otáčejícího se spolu s kolotočem
Z pohledu neinerciálního pozorovatele otáčejícího se spolu s kolotočem je závaží v klidu.
Jaké síly na závaží působí?
Tah vlákna \(\vec{F}_\mathrm{T}\)
Tíhová síla \(\vec{F}_\mathrm{G}\)
To jsou reálné síly, kde najdeme dva původce, kteří na sebe vzájemně působí (vlákno–závaží; Země–závaží). Má-li být výslednice sil nulová, musíme přidat ještě sílu, která účinky tíhové síly a tahu vlákna kompenzuje: setrvačnou odstředivou sílu \(\vec{F}_\mathrm{od}\) (u této síly najdeme jen na co působí, ale „pachatele“ nikoliv).
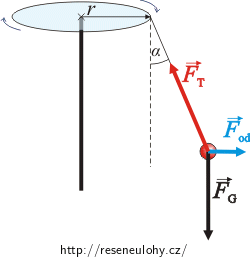
Jak bylo výše řečeno, je závaží z pohledu neinerciálního pozorovatele otáčejícího se spolu s kolotočem v klidu. Výslednice sil na ně působících musí být tedy rovna nule:
\[\sum{\vec{F}} = 0.\]Dosadíme-li síly známé z náčrtku, tedy tah vlákna \(\vec{F}_\mathrm{T}\), tíhovou sílu \(\vec{F}_\mathrm{G}\) a setrvačnou odstředivou sílu \(\vec{F}_\mathrm{od}\), dostáváme vektorovou rovnici:
\[\vec{F}_\mathrm{T} + \vec{F}_\mathrm{G} + \vec{F}_\mathrm{od} = 0.\]Přepíšeme ji skalárně. Souřadný systém volíme podle obrázku.
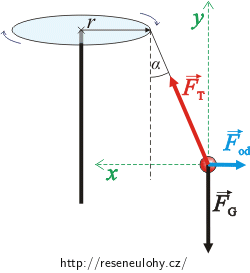
Vodorovný směr (osa x):
\[{F}_\mathrm{T}\sin\alpha = {F}_\mathrm{od}.\]Svislý směr (osa y):
\[{F}_\mathrm{T}\cos\alpha = mg.\]Po úpravě a dosazení z druhé rovnice za FT do první dostáváme:
\[mg \mathrm{tg}\alpha = {F}_\mathrm{od}.\]Připomeňme si vztahy pro setrvačnou odstředivou sílu působící při pohybu po kružnici o poloměru ρ v závislosti na úhlové rychlosti ω a vztah mezi úhlovou rychlostí a periodou pohybu T:
\[{F}_\mathrm{od} = m\omega^2\rho,\] \[\omega = \frac{2\pi}{T}.\]Dosadíme do předchozí rovnice:
\[mg \mathrm{tg}\alpha = m\omega^2\rho,\] \[g \mathrm{tg}\alpha = \omega^2\rho,\] \[g \mathrm{tg}\alpha = \frac{4\pi^2}{T^2} \rho.\]Odtud:
\[ T^2 = 4\pi^2\frac{\rho}{g \mathrm{tg}{\alpha}},\] \[ T = 2\pi \sqrt{\frac{\rho}{g \mathrm{tg}{\alpha}}}.\]Poloměr kružnice ρ, po které závaží obíhá, je dán součtem vzdálenosti upevnění závěsu r od osy kolotoče a vzdálenosti rα vzniklé vykývnutím závaží délky l ze svislé klidové polohy o úhel α.
Platí tedy:
\[\rho = r+r_\alpha = r + l\sin\alpha.\]Odtud dostáváme výsledný vztah:
\[ T = 2\pi \sqrt{\frac{r + l\sin\alpha}{g \mathrm{tg}{\alpha}}}.\]Číselně:
\[ T = 2\pi \sqrt{\frac{2 + 1 \mathrm{sin}10^{\circ}}{9{,}81 \mathrm{tg}10^{\circ}}}\,\mathrm{s} = 7\,\mathrm{s}.\]



