Tyč na půlválci
Úloha číslo: 1251
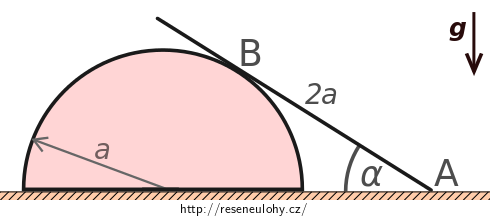
Homogenní tyč délky \(2a\) se opírá koncem \(\mathrm{A}\) o hladkou podlahu. Kromě toho se ještě opírá o válcovou plochu kruhového průřezu o poloměru \(a\) (viz obr.).
V bodě \(\mathrm{B}\) na tyč také působí třecí síla \(T\), která zabraňuje sklouznutí.
Jaká je její velikost, svírá-li tyč s podlahou úhel \(\alpha\)?
Jaký kritický úhel může tyč svírat s podlahou, aby ještě nesklouzla, je-li \(f\) koeficient tření mezi tyčí a válcovou plochou?
Rozbor
Tyč je o válcovou plochu opřená a je v klidu. To znamená, že součet na ni působících sil i jejich momentů musí být nutně nulový. Podmínky statické rovnováhy tělesa lze zapsat vektorovými rovnicemi \[\sum_{i=1}^n \vec{F_i} = \vec{0} \quad \wedge \quad \sum_{i=1}^n \vec{M_i} = \vec{0}. \tag{i}\] Moment \(\vec{M_i}\) síly \(\vec{F_i}\) je dán vektorovým součinem \[\vec{M_i} = \vec{r_i}\times \vec{F_i},\] kde \(\vec{r_i}\) je vektor s počátkem v libovolně zvoleném vztažném bodě a koncem v působišti vektoru síly \(\vec{F_i}\).Vzhledem k tomu, že všechny síly leží v jedné rovině, budou výsledné vektorové součiny představující momenty těchto sil ležet v jedné přímce.
Tření v bodě \(\mathrm{A}\) vzhledem k hladké podlaze zanedbáváme.
Třecí síla působící mezi tyčí a válcovou plochou kompenzuje opačnou, stejně velkou sílu, která se snaží o sklouznutí tyče. Bude-li se tato síla zvětšovat, bude stejně růst i třecí síla a to až k dosažení maximální hodnoty statického tření, dané součinitelem statického tření \(f\) a normálovou silou \(N\) pomocí vztahu
\[F{_t}_\mathrm{max} = f N,\] \[ \mathrm{tj.}\quad F_t \le f N.\tag{ii}\] V naší úloze hledáme kritický úhel, při které tyč ještě nespadne, tj. budeme hledat úhel, kdy odpovídající třecí síla potřebná k udržení rovnováhy vyhovuje rovnici (ii).Zápis
\(a\) poloměr válcové plochy \(2a\) délka homogenní tyče \(\alpha\) úhel, který svírá tyč s podložkou \(f\) součinitel klidového tření v \(\mathrm{B}\)
\(T = \mathrm{?}\) velikost třecí síly v \(\mathrm{B}\) \(\alpha^\prime = \mathrm{?}\) kritický úhel pro dané \(f\) Nápověda 1 – působící síly
Zakreslete do obrázku všechny síly, které na tyč působí.
Dbejte na správné určení jejich působišť. V případě tíhové síly si uvědomte, že tyč je homogenní. Kromě třecí a tíhové síly neopomeňte, že na tyč působí reakčními silami jak podložka, tak opěrný válec.
Nápověda 2 – zavedení soustavy souřadnic
Pokuste se vhodně zavést kartézskou soustavu souřadnic \({Oxy}\).
Nápověda 3 – podmínky rovnováhy
Čemu musí být rovna výslednice všech sil a výslednice všech momentů sil působících na tyč, je-li tyč v klidu, tj. neposouvá se, neotáčí se?
Zapište vektorově rovnice vyjadřující podmínky statické rovnováhy.
Nápověda 4 – skalární rovnice, třecí síla
Vektorové rovnice přepište do skalární podoby. Ze vzniklé soustavy tří skalárních rovnic o třech neznámých vyjádřete neznámou třecí sílu \(T\).
Nápověda 5 – kritický úhel
Uvažujte prvotní situaci, kdy je tyč v klidu.
Sklouznutí tyče zamezuje třecí síla v bodě \(\mathrm{B}\). Budeme-li nyní konec tyče \(\mathrm{A}\) posouvat směrem vlevo, bude se zvětšovat úhel \(\alpha\) a s ním i požadavek na velikost třecí síly v bodě styku tyče s válcovou plochou. Statická třecí síla mezi tyčí a plochou je však omezena maximální hodnotou, která je dána součinitelem statického tření a přítlačnou silou.
Pokuste se užitím znalosti závislostí \(T(\alpha)\) (T) a \(R_2(\alpha)\) (II) určit maximální úhel \(\alpha\), při kterém tyč ještě nesklouzne.
Poznámka
V řešení nápovědy 3 jsme došli k následující podmínce pro úhel \(\alpha\):
\[ \alpha \le \mathrm{arctg}\, f. \]Tedy, že tyč nesklouzne, bude-li s podlahou svírat úhel menší než \(\mathrm{arctg}\, f\).
Nesmíme zapomenout, že toto řešení vychází z pohybových rovnic řešených pro případ, že v bodě \(\mathrm{B}\) je pravý úhel. Ten je tam pouze tehdy, je-li tyč opřená tečně. Případ nejmenšího úhlu, při kterém je tyč ještě tečnou, zachycuje následující obrázek.
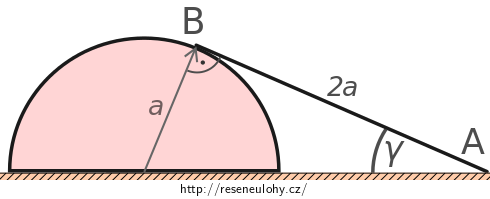
Pro minimální úhel \(\gamma\), při kterém je tyč ještě tečnou, platí
\[\mathrm{tg}\, \gamma = \frac{a}{2a} = \frac{1}{2} \quad \Longrightarrow \quad \gamma = \mathrm{arctg}\,\frac{1}{2} .\]Svůj závěr tedy upřesníme. Tyč nepodklouzne pro úhel \(\alpha\), který splňuje podmínku
\[\mathrm{arctg}\, \frac{1}{2} \le \alpha \le \mathrm{arctg}\, f.\]Z této podmínky je zřejmé, že nebude-li součinitel \(f\) dostatečně velký, tj. pokud
\[\mathrm{arctg}\, f \lt \mathrm{arctg}\, \frac{1}{2},\]nebude existovat žádná tečná poloha opření tyče, při které by tyč nepodklouzla.
Pro zjištění chování pro úhly \(\alpha \lt \mathrm{arctg}\,\frac{1}{2}\) bychom museli vytvořit nové rovnice statické rovnováhy.
V zadání je však řečeno, že tyč je tečně opřena (nepodkluzuje). To znamená, že existuje minimálně jedna poloha tečného opěru. Musí tedy existovat mezní úhel, při kterém tyč ještě nepodklouzne. Je dán vztahem \[\alpha' = \mathrm{arctg}\, f,\] přičemž při větších úhlech tyč již sklouzne.CELKOVÉ ŘEŠENÍ
Do obrázku zakreslíme všechny síly, které na tyč působí.Síly působící na tyč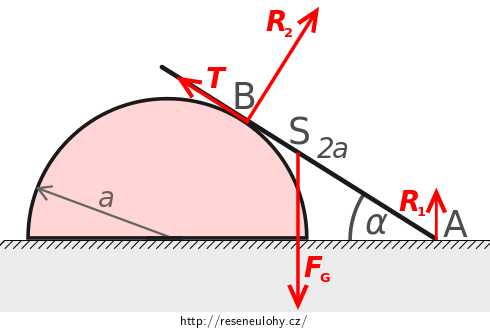
Protože je tyč homogenní, působí na ni tíhová síla \(\vec{F_\mathrm{G}}\) v jejím těžišti, které odpovídá geometrickému středu tyče. Síla směřuje svisle dolů.
Třecí síla \(\vec{T}\) působí v místě dotyku tyče a válcové plochy v tečném směru, je orientována proti zamýšlenému pohybu tyče.
V místech dotyku tyče s podložkou a válcovou plochou působí na tyč v normálovém směru k dotyčným plochám reakční síly \(\vec{R_1}\) a \(\vec{R_2}\).
Soustavu souřadnic můžeme zavést dle následujícího obrázku.
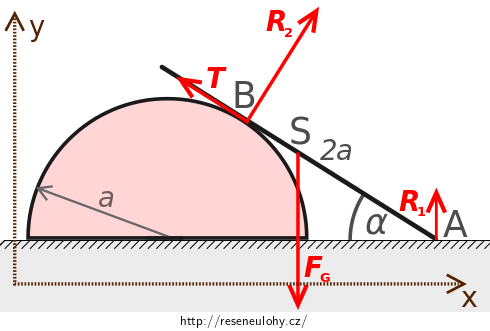
Podmínky rovnováhy
Tyč není v žádném směru urychlována. Výslednice všech sil působících na tyč je nutně nulová. Tedy
\[\vec{T\,}+\vec{F_\mathrm{G}} + \vec{R_1} + \vec{R_2} = \vec{0}.\tag{1}\]Tyč se neroztáčí. Výslednice všech na tyč působících momentů sil je nutně nulová. Momentová věta vzhledem k bodu \(\mathrm{A}\) má tvar
\[\overset{\longrightarrow}{\mathrm{AB}}\times\vec{T\,} + \overset{\longrightarrow}{\mathrm{AS}}\times\vec{F_\mathrm{G}} + \vec{0}\times\vec{R_1} + \overset{\longrightarrow}{\mathrm{AB}}\times\vec{R_2} = \vec{0}.\tag{2}\]Rozklad sil do směrů soustavy souřadnic
Z obrázku jsou zřejmé souřadnice vektorů sil vůči zavedené soustavě \(Oxy\): \[\vec{T\,} = \left(-T\cos{\alpha}\,,\,T\sin{\alpha} \right),\qquad \vec{F_\mathrm{G}} = \left(0\,,\,-F_\mathrm{G}\right),\] \[\vec{R_1} = \left(0\,,\,R_1\right), \qquad \vec{R_2} = \left(R_2\sin{\alpha}\,,\,R_2\cos{\alpha}\right).\] Vektory dosadíme do rovnice (1), získáme vektorovou rovnici: \[ \left(-T\cos{\alpha}\,,\,T\sin{\alpha} \right) + \left(0\,,\,-F_\mathrm{G}\right) + \left(0\,,\,R_1\right)+ \left(R_2\sin{\alpha}\,,\,R_2\cos{\alpha}\right) = (0\,,\,0), \] která v sobě skrývá pro složky dvě skalární rovnice: \[ \begin{eqnarray} R_2\sin\alpha - T\cos \alpha & = & 0~, \tag{3} \\ R_1 - F_\mathrm{G} + R_2\cos\alpha + T\sin\alpha & = & 0~.\tag{4} \end{eqnarray} \]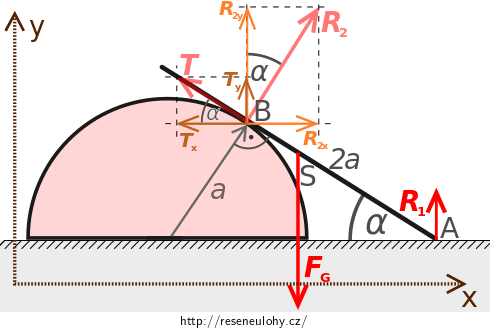
Výsledné vektory všech vektorových součinů v rovnici (2) leží na přímce, lze tedy sčítat jejich velikosti opatřené znaménkem dle směru. Než napíšeme momentovou rovnici skalárně, vyjádříme si velikosti jednotlivých vektorových součinů:
\[ \begin{eqnarray} |\overset{\longrightarrow}{AB}\times \overset{\rightarrow}{T}| & = & |\overset{\longrightarrow}{AB}| |\overset{\rightarrow}{T\,}|\,\sin{0}=0~,\\ |\overset{\longrightarrow}{AS}\times \overset{\rightarrow}{F_\mathrm{G}}| & = & |\overset{\longrightarrow}{AS}| |\overset{\rightarrow}{F_\mathrm{G}}|\,\sin{\left(90^\mathrm{\circ} - \alpha \right)}=a\,F_\mathrm{G}\cos\alpha \quad~\odot~,\\ |\overset{\rightarrow}{\,0}\times \overset{\rightarrow}{R_1}| & =& 0~,\\ |\overset{\longrightarrow}{AB}\times \overset{\longrightarrow}{R_2}|&=& |\overset{\longrightarrow}{AB}| |\overset{\longrightarrow}{R_2}|\,\sin{90^\mathrm{\circ}}=a\,\mathrm{cotg}\,{\alpha}\,R_2 {\cdot} 1 = a\, R_2\mathrm{cotg}\,\alpha \quad~\otimes~. \end{eqnarray} \] Poslední vyjádření má omezenou platnost, viz poznámka.Velikosti součinů jsou označeny
\(\odot\) směřuje-li vektorový součin před nákresnu,\(\otimes\) směřuje-li vektorový součin za nákresnu.Přihlédneme k orientaci vektorových součinů a opatříme jejich velikosti znaménkem. Rovnice (2) tak přejde ve skalární rovnici:
\[ \begin{eqnarray} a F_\mathrm{G}\cos\alpha - aR_2\mathrm{cotg}\,\alpha & = & 0~ \qquad |\cdot {a}^{-1},\\ F_\mathrm{G}\cos\alpha - R_2\mathrm{cotg}\,\alpha & = & 0~. \tag{5} \end{eqnarray} \]Rovnice (3), (4) a (5) jsou tři rovnice o třech neznámých \(R_1, R_2\) a \(T\). Hledáme pouze velikost třecí síly – postačí nám proto nalézt neznámou \(T\).
Z rovnice (3) vyjádříme \(R_2\):
\[R_2 = T\frac{\cos \alpha}{\sin\alpha} = T\mathrm{cotg}\,\alpha~.\tag{I}\]Z rovnice (5) vyjádříme \(R_2\):
\[R_2 = F_\mathrm{G}\frac{\cos\alpha}{\mathrm{cotg}\, \alpha} = F_\mathrm{G} \sin\alpha~. \tag{II}\]Vyloučením \(R_2\) z rovnic (I) a (II) získáme rovnost, odkud snadno vyjádříme hledané \(T\):
\[ \begin{eqnarray} T\mathrm{cotg}\, \alpha &=& F_\mathrm{G} \sin\alpha,\\ \quad & \Rightarrow & T = F_\mathrm{G} \frac{\sin\alpha}{\mathrm{cotg}\, \alpha} = F_\mathrm{G} \mathrm{tg}\, \alpha \sin\alpha. \tag{T} \end{eqnarray} \]
Kritický úhel Při řešení předpokládáme, že pro dané \(f\) existuje rozsah úhlů \(\alpha\), při kterých je možné bez podklouznutí tyč tečně opřít.Velikost statické třecí síly je limitována její maximální hodnotou, která závisí na součiniteli smykového tření pro styčné plochy a přítlačné síle, tj.
\[T \le fR_2.\] Dosazením požadované velikosti třecí síly (T) a přítlačné síly (II) v závislosti na úhlu \(\alpha\) získáme \[ \begin{eqnarray} F_\mathrm{G} \mathrm{tg}\, \alpha \sin \alpha &\le& f F_\mathrm{G} \sin \alpha\quad|\cdot {\left(F_\mathrm{G} \sin \alpha\right)}^{-1}\\ \mathrm{tg}\, \alpha &\le& f\\ \\ & \Longrightarrow & \alpha \le \mathrm{arctg}\, f. \end{eqnarray} \] Mezním úhlem, při kterém tyč ještě nesklouzne, je úhel \[\alpha' = \mathrm{arctg}\, f,\] při větších úhlech tyč sklouzne.Odpověď
Velikost třecí síly při tečném opření tyče délky \(2a\) a hmotnosti \(m\) o válcovou plochu s poloměrem \(a\) je dána vztahem \(T = F_\mathrm{G} \mathrm{tg}\, \alpha \sin \alpha,\)
kde \(\alpha\) je odchylka tyče od vodorovné roviny.-
Odchylku \(\alpha\) tyče od vodorovné podložky lze zvětšovat až do mezní hodnoty \(\alpha' = \mathrm{arctg}\, f\). Po jejím překročení dojde k proklouznutí tyče.
Odkaz na podobné úlohy
Pokud jste nalezli zalíbení v opřených homogenních tyčích o různá tělesa nebo si chcete tento typ příkladů procvičit, můžete zkusit vyřešit některou z následujících, neméně zajímavých úloh



