Vytékání vody z nádoby (aneb když vyndáme špunt)
Úloha číslo: 1154
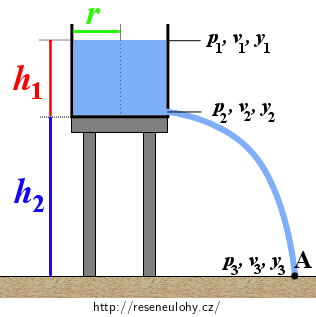
Válcová nádrž o poloměru 90 centimetrů stojí na podstavci vysokém 6 metrů a je do výšky 3 metry naplněna vodou. U dna je nádrž utěsněna zátkou o plošném obsahu 6,3 cm2. Určete:
- Jakou rychlostí dopadne proud vody na zem, když zátku odstraníme.
- Jak dlouho potrvá, než se nádoba zcela vyprázdní.
Zápis
r = 0,90 m poloměr válcové nádrže h1 = 3 m výška hladiny vody v nádrži h2 = 6 m výška podstavce S2 = 6,3 cm2 obsah plochy zátky v3 = ? rychlost, s jakou dopadne proud vody na zem t = ? čas, za který se nádrž zcela vyprázdní Rozbor
K řešení 1. části úlohy můžeme využít Bernoulliho rovnici. Buď ji lze napsat pro situaci u hladiny a u země, nebo pro situaci u hladiny a u dna nádoby – v tomto případě musíme ještě ke zjištění rychlosti dopadu na zem použít poznatky o vodorovném vrhu.
Ve 2. části úlohy použijeme rovnici kontinuity – za jednotku času poklesne objem vody v nádrži o to, co z ní vyteče. Musíme si ale uvědomit, že rychlost výtoku ani poklesu hladiny vody není konstantní, ale záleží na výšce hladiny v nádrži. Budeme proto pracovat s poklesy o velmi malou výšku dh za kratičký čas dt, během kterého budeme považovat výtokovou rychlost za konstantní. Celkový čas pak získáme integrací příslušné rovnice.
Nápověda 1 – k části a.
Vyjděme ze skutečnosti, že v okamžiku odstranění zátky začíná voda z nádrže proudit. Která rovnice popisující proudění by nám mohla pomoci při výpočtu rychlosti?
Nápověda 2 - k části a.
Nyní rozepište Bernoulliho rovnici pro:
- vodní hladinu,
- bod A, kde proud vody dopadá na zem (zde také volte nulové y).
Které členy z rovnice vymizí? Ze zbylých členů již přímo vyjádřete hledanou rychlost v3 a číselně dopočtěte.
Nápověda 3 – k části b.
Vyjděte z jednoduché úvahy, která říká, že za jednotku času se zmenší objem vody v nádrži právě o objem, který vyteče ven. Napište pro tuto situaci rovnici kontinuity.
Nápověda 4 – k části b.
Zamyslete se nad tím, zda jsou rychlosti vystupující v rovnici kontinuity stálé či ne a jak se s tím vypořádat. Obě rychlosti pak vyjádřete.
Nápověda 5 – k části b.
Nyní dosaďte ze vztahů (8) a (10) do rovnice kontinuity (7) a vyřešte vzniklou diferenciální rovnici se separovanými proměnnými. Integrací ve správných mezích dostanete celkový čas vyprazdňování nádrže t.
Celkové řešení
Část a:
Protože po odstranění zátky začíná voda proudit, využijeme k řešení naší úlohy Bernoulliho rovnici. Pro ustálené proudění má tato rovnice následující tvar:
\[p\,+\,y{\varrho}g\,+\,\frac{1}{2}{\varrho}v^2\,=\,c\,\,(c\,=\,konst.), \tag{1}\]kde p je vnější tlak, y výška nad zvolenou nulovou hladinou, ρ hustota proudící kapaliny (plynu), g tíhové zrychlení a v rychlost proudění. Bernoulliho rovnice je důsledkem zákona zachování energie, a tak lze první člen nalevo interpretovat jako potenciální tlakovou energii, druhý jako potenciální tíhovou energii a třetí jako kinetickou energii, vše vztaženo na jednotkový objem proudící kapaliny (plynu). Součet těchto „objemových hustot energie“ zůstává roven konstantě c.
Vyjádříme levou stranu rovnice (1) pro:
- vodní hladinu (veličiny s indexem 1),
- bod A (veličiny s indexem 3).
Protože obě tyto levé strany jsou rovny konstantě c, lze je položit do rovnosti:
\[p_1\,+\,y_1{\varrho}g\,+\,\frac{1}{2}{\varrho}v_1^2\,=\,p_3\,+\,y_3{\varrho}g\,+\,\frac{1}{2}{\varrho}v_3^2,\tag{2}\]kde ρ je hustota vody. Pojďme nyní diskutovat některé veličiny ze vztahu (2):
- Vnější tlak, který v obou případech působí, je roven pouze atmosférickému tlaku: \[p_1\,=\,p_3\,=\,p_\mathrm{a}.\tag{3}\] (Zanedbáváme rozdíl atmosférického tlaku mezi hladinou vody a bodem A, jeho velikost je o několik řádů menší než další hodnoty ve vztahu (2).)
- Bod A leží v nulové výšce, proto je: \[y_3\,=\,0.\tag{4}\]
- Hladina má vzhledem ke zvolené nulové hladině výšku: \[y_1\,=\,h_1\,+\,h_2.\tag{5}\]
- U hladiny se voda v okamžiku uvolnění zátky téměř nepohybuje, tedy: \[v_1\,=\,0.\tag{6}\]
Dosazením vztahů (3) až (6) do rovnice (2) dostáváme:
\[p_\mathrm{a}\,+\,(h_1\,+\,h_2){\varrho}g\,=\,p_\mathrm{a}\,+\,\frac{1}{2}{\varrho}v_3^2\,\Rightarrow\,v_3\,=\,\sqrt{2g(h_1\,+\,h_2)}.\]Číselně:
\[v_3\,=\,\sqrt{2{\cdot}9{,}81{\cdot}(3\,+\,6)}\,\mathrm{m}{\cdot}\mathrm{s^{-1}}\,=\,13{,}3\,\mathrm{m}{\cdot}\mathrm{s^{-1}}.\]Část b:
Vyjdeme z jednoduché úvahy, která říká, že za jednotku času se zmenší objem vody v nádrži právě o objem, který vyteče ven. To vede přímo k myšlence využít při výpočtu rovnici kontinuity ve tvaru:
\[S_1v_1\,=\,S_2v_2,\tag{7}\]kde S1 je plošný obsah kruhové podstavy nádrže, v1 rychlost poklesu hladiny, S2 plošný obsah zátky a v2 rychlost vody vytékající otvorem po zátce ven. Z pouhého náhledu je ale patrné, že rychlosti v1, v2 nejsou během vyprazdňování nádrže konstantní. Čím bude hladina v nádrži níže, tím pomaleji bude voda ven vytékat, což zpětně zpomalí další pokles hladiny. V rovnici kontinuity se tedy budeme muset zaměřit na pokles hladiny o infinitezimální element dh za čas dt, pro který bude výtoková rychlost v2 při dané výšce hladiny h konstantní:
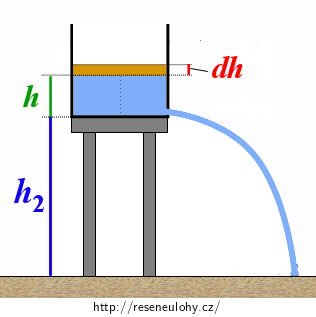
Protože rychlost poklesu hladiny v1 je infinitezimálně malá, lze pro ni psát:
\[v_1\,=\,-\frac{\mathrm{d}h}{\mathrm{d}t}.\tag{8}\]Znaménko minus vstupuje do výrazu výše proto, že rychlost v1 je samozřejmě kladná, ale výška hladiny klesá, tedy derivaci dh/dt je záporná. Výtokovou rychlost v2 určíme pomocí Bernoulliho rovnice, kterou napíšeme pro hladinu vody v aktuální výšce h a pro otvor po zátce. Opět předpokládáme, že při hladině se voda nepohybuje, infinitezimální pokles hladiny zde vzhledem k velikosti výtokové rychlosti můžeme zanedbat. Platí tedy:
\[p_\mathrm{a}\,+\,(h_2\,+\,h){\varrho}g\,=\,p_\mathrm{a}\,+\,h_2{\varrho}g\,+\,\frac{1}{2}{\varrho}v_2^2.\tag{9}\]Odtud dostáváme:
\[v_2\,=\,\sqrt{2gh}.\tag{10}\]Dosazením vztahů (8) a (10) do rovnice kontinuity (7) dostáváme:
\[-\frac{\mathrm{d}h}{\sqrt{h}}\,=\,{\sqrt{2g}}\frac{S_2}{S_1}\mathrm{d}t.\]Což je lineární diferenciální rovnice s konstantními koeficienty, jejíž proměnné lze separovat:
\[-\frac{\mathrm{d}h}{\sqrt{h}}\,=\,{\sqrt{2g}}\frac{S_2}{S_1}\mathrm{d}t.\]Celou rovnici zintegrujeme v příslušných mezích:
\[-\int_{h_1}^0\frac{\mathrm{d}h}{\sqrt{h}}\,=\,\int_0^t{\sqrt{2g}}\frac{S_2}{S_1}\mathrm{d}t.\tag{12}\]Pro celkovou dobu vyprazdňování nádoby tedy dostáváme:
\[2\sqrt{h_1}\,=\,{\sqrt{2g}}\frac{S_2}{S_1}t\,\Rightarrow\,t\,=\,\frac{S_1}{S_2}\sqrt{\frac{2h_1}{g}}.\tag{13}\]Za obsah S1 dosadíme obsah kruhu o poloměru r a číselně vyjádříme:
\[t\,=\,\frac{{\pi}{\cdot}0{,}9^2}{6{,}3{\cdot}10^{-4}}\sqrt{\frac{2{\cdot}3}{9{,}81}}\,\mathrm{s}\,\dot=\,3160\,\mathrm{s}\,\dot=\,52{,}7\,\mathrm{min}.\]Alternativní řešení části a.
Část a) můžeme vyřešit také pomocí znalostí o vodorovném vrhu. Stejným postupem jako v části b), tj. Bernoulliho rovnicí, určíme výtokovou rychlost z nádrže v2, která je těsně po vyjmutí zátky rovna:
\[v_2\,=\,\sqrt{2gh_1}.\]Tato rychlost má v místě, kde opouští nádobu, směr kolmý na její stěnu, jde tedy vlastně o vodorovnou složku vx rychlosti vodorovného vrhu, která se během vrhu nemění:
\[v_\mathrm{x}\,=\,v_2.\]Svislou komponentu vy určíme z kinematického popisu volného pádu z výšky h2:
\[v_\mathrm{y}\,=\,gt\,=\,g\sqrt{\frac{2h_2}{g}}\,=\,\sqrt{2gh_2}.\]Pro celkovou velikost rychlosti dopadu proudu vody v3 pak platí:
\[v\,=\,\sqrt{v_\mathrm{x}^2\,+\,v_\mathrm{y}^2}\,=\,\sqrt{2g(h1\,+\,h_2)},\]což je tvar shodný s výrazem získaným již dříve uvedeným postupem.
Odpověď
Rychlost proudu vody, se kterou po vyjmutí zátky dopadne na zem, je přibližně 13,3 m·s−1. Celá nádrž se vyprázdní za 52,7 minuty.




