Krasobruslaři
Úloha číslo: 84
Dvojici krasobruslařů tvoří partner o hmotnosti 75 kg a partnerka o hmotnosti 50 kg. Oba stojí na ledě těsně za sebou, partnerka vpředu a partner vzadu. Nyní se partner rukama opře o záda partnerky a stálou silou o velikosti 120 N ji odstrkuje po dobu 0,50 s. Žádný z bruslařů se nebrání pohybu, tření zanedbejte.
a) Určete velikost vzájemné rychlosti bruslařů po odstrčení.
b) Určete práci vykonanou partnery během odstrkování.
c) Nyní si partneři vymění role. To znamená, že partnerka stojí za partnerem a působí na záda partnera stejně velkou silou a po stejnou dobu. Jak se změní výsledky úloh a), b)?
d) Nyní opět stojí partner za partnerkou jako v původním zadání, ale je opřen zezadu o mantinel. Jak se změní výsledek úloh a), b)?
Zápis
m1 = 75 kg hmotnost partnera m2 = 50 kg hmotnost partnerky F = 120 N síla, kterou partner odstrkuje partnerku Δt = 0,50 s doba, po kterou partner odstrkuje partnerku v = ? m·s−1 vzájemná rychlost bruslařů po odstrčení W = ? J práce vykonaná partnery Nápověda a – Vzájemná rychlost krasobruslařů
Nakreslete si obrázek. Zjistěte, jakou rychlost bude mít po odstrčení každý z partnerů. Využijte k tomu vztah, který platí mezi impulsem síly a změnou hybnosti.
Nápověda b – vykonaná práce
Vykonaná práce je rovna energii, kterou bruslaři získají při uvedení do pohybu. Jaká je to energie? Vyjádřete ji pomocí vzorce.
Nápověda c – vyměněné role
Uvědomte si, co říká třetí Newtonův zákon.
Nápověda d – mantinel
Nakreslete si obrázek. Jak se změní hybnost partnera, jestliže je opřený o mantinel?
Číselný výpočet
Je dáno:
\[m_1\,=\,75 \,\mathrm {kg}\] \[m_2\,=\,50 \,\mathrm {kg}\] \[F\,=\,120 \,\mathrm {N}\] \[\mathrm{\Delta} t\,=\,0{,}50 \,\mathrm {s}\]
a) Hledáme:
\[v\,=\,?\] \[v\,=\,\frac{m_1+m_2}{m_1m_2}\,F\,\mathrm{\Delta} t\,=\,\frac{75+50}{75{\cdot}50}120{\cdot}0{,}5\,\mathrm{m \cdot s^{-1}}\] \[v\,=\,2\,\mathrm{m \cdot s^{-1}}\]b) Hledáme:
\[W\,=\,?\] \[W\,=\,\frac{m_1+m_2}{2m_1m_2}\,F^2\,(\mathrm{\Delta} t)^2\,=\,\frac{75+50}{2{\cdot}75\cdot50}\,120^2\,\cdot0{,}5^2\,\mathrm{J}\] \[W\,=\,60\,\mathrm{J}\]c) Výsledky úloh a), b) se nezmění.
d) Hledáme:
\[v^{'}\,=\,?\] \[W^{'}\,=\,?\] \[v^{'}\,=\,\frac{F\mathrm{\Delta} t}{m_2}\,=\,\frac{120{\cdot}0{,}5}{75}\mathrm{m \cdot s^{-1}}\] \[v^{'}\,=\,1{,}2\,\mathrm{m \cdot s^{-1}}\] \[W^{'}\,=\,\frac{F^2(\mathrm{\Delta} t)^2}{2m_2}\,=\,\frac{120^2{\cdot}0{,}5^2}{2{\cdot}75}\,\mathrm{J}\] \[W^{'}\,=\,36\,\mathrm{J}\]Odpověď
a) Velikost vzájemné rychlosti krasobruslařů je \[v\,=\,\frac{m_1+m_2}{m_1m_2}F\mathrm{\Delta} t\,=\,2\,\mathrm{m \cdot s^{-1}}.\]
b) Práce vykonaná partnery během odstrkování je \[W\,=\,\frac{m_1+m_2}{2m_1m_2}F^2(\mathrm{\Delta} t)^2\,=\,60\,\mathrm{J}.\]
c) Výsledky úloh a), b) se nezmění.
d) Velikost vzájemné rychlosti v případě, že partner je opřen zezadu o mantinel, je \[v^{'}\,=\,\frac{F\mathrm{\Delta} t}{m_2}\,=\,1{,}2\,\mathrm{m \cdot s^{-1}}.\]
Vykonaná práce je v tomto případě rovna \[W^{'}\,=\,\frac{F^2(\mathrm{\Delta} t)^2}{2m_2}\,=\,36\,\mathrm{J}.\]
Celkové řešení bodu a) – hybnost krasobruslařů

m1…hmotnost partnera
m2…hmotnost partnerky
Impuls síly je roven časové změně hybnosti. V našem případě je působící síla konstantní a působí ve směru posunutí partnerů, takže vztah můžeme napsat ve tvaru:
\[F\mathrm{\Delta} t\,=\,\mathrm{\Delta} p\,.\]Pro partnerku tedy platí:
\[F\mathrm{\Delta} t\,=\, p_2-p_0\,.\]F…síla, kterou partner působí na partnerku
p2…hybnost partnerky po odstrčení
p0…počáteční hybnost partnerky (p0 = 0)
\[F\mathrm{\Delta} t\,=\,m_2v_2\]v2…rychlost partnerky po odstrčení
Odsud si vyjádříme rychlost partnerky v2:
\[v_2\,=\,\frac{F\mathrm{\Delta} t}{m_2}\,.\tag{1}\]Velikost síly, kterou působí partnerka na partnera, je podle třetího Newtonova zákona stejně velká jako velikost síly, kterou působí on na ni, a je tedy rovna F.
Pro partnera platí:
\[F\mathrm{\Delta} t\,=\, p_1-p_0^{'}\,.\]F…síla, kterou partnerka působí na partnera
p1…hybnost partnera po odstrčení
\(p_0^{'}\)…počáteční hybnost partnera (\(p_0^{'}\) = 0)
\[F\mathrm{\Delta} t\,=\,m_1v_1\]v…rychlost partnera po odstrčení
Odsud si vyjádříme rychlost partnera v1:
\[v_1\,=\,\frac{F\mathrm{\Delta} t}{m_1}\,.\tag{2}\]Vzájemná rychlost krasobruslařů je rovná součtu rychlosti partnera a partnerky.
\[v\,=\,v_1+v_2\,.\]\(v\)…vzájemná rychlost krasobruslařů
Dosazením za rychlosti v1, v2 ze vztahů (1),(2) dostaneme:
\[v\,=\,\frac{F\mathrm{\Delta} t}{m_1}\,+\,\frac{F\mathrm{\Delta} t}{m_2},\] \[v\,=\,\frac{m_1\,+\,m_2}{m_1 m_2}\,F\mathrm{\Delta} t,\] \[v\,=\,\frac{75+50}{75{\cdot}50}\,120\,\cdot0{,}5\,\mathrm{m \cdot s^{-1}},\] \[v\,=\,2\,\mathrm{m \cdot s^{-1}}.\]Odpověď: Velikost vzájemné rychlosti krasobruslařů je \[v\,=\,\frac{m_1+m_2}{m_1m_2}F\mathrm{\Delta} t \,=\, 2\,\mathrm{m \cdot s^{-1}}.\]
Celkové řešení bodu b) – vykonaná práce
Při uvedení do pohybu vzroste kinetická energie každého krasobruslaře. Vykonaná práce je rovna součtu kinetických energií obou krasobruslařů. (Případné změny vnitřní energie neuvažujeme.)
\[W\,=\,E_\mathrm{k1}+E_\mathrm{k2}\,.\]W… vykonaná práce
Ek1… kinetická energie partnera
Ek2… kinetická energie partnerky
\[W\,=\,\frac{1}{2}\,m_1v_1^2\,+\,\frac{1}{2}\,m_2v_2^2\]Za rychlosti v1 a v2 dosadíme ze vztahů (1) a (2):
\[W\,=\,\frac{1}{2}m_1\frac{F^2(\mathrm{\Delta} t)^2}{m_1^2}\,+\,\frac{1}{2}m_2\frac{F^2(\mathrm{\Delta} t)^2}{m_2^2},\] \[W\,=\,\frac{1}{2}\,F^2 \left(\mathrm{\Delta} t\right)^2\,\frac{\left(m_1+m_2\right)}{m_1m_2},\] \[W\,=\,\frac{75+50}{2{\cdot}75\cdot50}\,120^2\,\cdot0{,}5^2\,\mathrm{J},\] \[W=60\,\mathrm{J}.\]Poznámka:
Vykonanou práci lze určit i pomocí druhého Newtonova zákona a užitím vztahu pro dráhu rovnoměrně zrychleného pohybu.
Partnerka se během působení síly pohybuje s konstantním zrychlením o velikosti:
\[a_2\,=\,\frac{F}{m_2}\,.\tag{i}\]a2… zrychlení partnerky
Rovnoměrně zrychleným pohybem tak urazí dráhu:
\[s_2\,=\,\frac{1}{2}a_2(\mathrm{\Delta} t)^2\,.\tag{ii}\]s2… dráha, o kterou se partnerka posune vzhledem k ledu
Za zrychlení a2 dosadíme ze vztahu (i):
\[s_2\,=\,\frac{1}{2}\frac{F}{m_2}(\mathrm{\Delta} t)^2\,.\]Během odstrkování působí partnerka na partnera také silou o velikosti F.
Partner se pohybuje se zrychlením:
\[a_1\,=\,\frac{F}{m_1}\,.\tag{iii}\]a1… zrychlení partnera
Rovnomerně zrychleným pohybem urazí dráhu:
\[s_1\,=\,\frac{1}{2}a_1(\mathrm{\Delta} t)^2\,.\tag{iv}\]s1… dráha, o kterou se partner posune vzhledem k ledu
Za zrychlení a1 dosadíme ze vztahu (iii):
\[s_1\,=\,\frac{1}{2}\frac{F}{m_1}(\mathrm{\Delta} t)^2\,.\]Celková práce vykonaná partnery bude rovna:
\[W\,=\,Fs_1\,+\,Fs_2,\] \[W\,=\,F\,\frac{1}{2}\,\frac{F}{m_1}\,\left(\mathrm{\Delta} t\right)^2\,+\,F\,\frac{1}{2}\,\frac{F}{m_2}(\mathrm{\Delta} t)^2,\] \[W\,=\,\frac{F^2}{2m_1}\,(\mathrm{\Delta} t)^2\,+\,\frac{F^2}{2m_2}\,\left(\mathrm{\Delta} t\right)^2,\] \[W\,=\,\frac{m_1+m_2}{2m_1m_2}\,F^2\,\left(\mathrm{\Delta} t\right)^2,\] \[W\,=\,\frac{75+50}{2{\cdot}75\cdot50}\,120^2\,\cdot0{,}5^2\,\mathrm{J},\] \[W\,=\,60\,\mathrm{J}.\]Odpověď: Celková práce vykonaná partnery během odstrkování je \[W\,=\,\frac{m_1+m_2}{2m_1m_2}\,F^2\,(\mathrm{\Delta} t)^2\,=\,60\,\mathrm{J}.\]
Celkové řešení bodu c) – vyměněné role
Třetí Newtonův zákon říká, že působení těles (v našem případě krasobruslařů) je vzájemné. Bude-li odstrkovat partnerka partnera sílou F, bude přitom partner na partnerku působit stejně velkou silou opačného směru a výsledný efekt bude stejný. Výsledky úloh a), b) se tedy nezmění.
Odpověď: Výsledky úloh a), b) se nezmění.
Celkové řešení bodu d) – mantinel
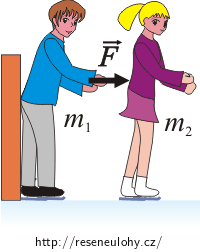
Partner působící sílou F po dobu Δt na partnerku (která byla na počátku v klidu), jí udělí hybnost o velikosti
\[p_2\,=\,F\mathrm{\Delta} t\,,\]ale sám zůstane na místě. Vzájemná rychlost bude rovna rychlosti partnerky.
\[m_2v_2\,\,=\,\,F\mathrm{\Delta} t\] \[v_2\,=\, \frac{F\mathrm{\Delta} t}{m_2}\] \[v^{'}\,=\,v_2\,=\,\frac{F\mathrm{\Delta} t}{m_2}\] \[v^{'}\,=\,\frac{120{\cdot}0{,}5}{75}\mathrm{ms^{-1}}\] \[v^{'}\,=\,1{,}2\,\mathrm{ms^{-1}}\]Vykonaná práce je rovna kinetické energii partnerky:
\[W^{'}\,=\,\frac{1}{2}m_2v_2^2\] \[W^{'}\,=\,\frac{1}{2}m_2\frac{F^2\left(\mathrm{\Delta} t\right)^2}{m_2^2}\,=\,\frac{F^2\left(\mathrm{\Delta} t\right)^2}{2m_2}\] \[W^{'}\,=\,\frac{120^2{\cdot}0{,}5^2}{2{\cdot}75}\mathrm{J}\] \[W^{'}\,=\,36\,\mathrm{J}\]Odpověď:
Velikost vzájemné rychlosti v případě, že partner je opřen zezadu o mantinel, je \(v^{'}\,=\,\frac{F\mathrm{\Delta} t}{m_2}\,=\,1{,}2\,\mathrm{ms^{-1}}\).
Vykonaná práce je rovna \(W^{'}\,=\,\frac{F^2\left(\mathrm{\Delta t}\right)^2}{2m_2}=36\,\mathrm{J}\).



