Bedna na nakloněné rovině s kladkou II
Úloha číslo: 1139
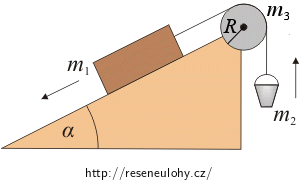
Za jakou dobu sjede bedna o hmotnosti m1 délku s po nakloněné rovině s úhlem sklonu α, je-li bedna pomocí provazu a kladky spojena s kbelíkem o hmotnosti m2? Vzájemný poměr m1/m2 je takový, že pohyb probíhá po nakloněné rovině směrem dolů. Tření a hmotnost provazu zanedbejte. Kladku považujte za homogenní válec o hmotnosti m3 a poloměru R.
Komentář
Seznamte se s řešením úlohy Bedna na nakloněné rovině s kladkou, která řeší zcela stejný problém, pouze se v ní zanedbává moment setrvačnosti kladky.
Nápověda 1
Jak se změní postup ukázaný v úloze Bedna na nakloněné rovině s kladkou, jestliže budeme uvažovat nenulový moment setrvačnosti kladky? Změní se tím nějak silové působení? Všechny působící síly zakreslete do obrázku a sestavte pohybové rovnice pro bednu, kyblík a kladku.
Nápověda 2
Vyjádřete v rovnici (3) výsledný moment sil působících na kladku vzhledem k jejímu středu. Rovnici pak přepište skalárně a dosaďte za moment setrvačnosti i úhlové zrychlení tak, aby v ní vystupovalo zrychlení bedny a.
Nápověda 3
Všechny pohybové rovnice sečtěte a vyjádřete z nich zrychlení a.
Nápověda 4
O jaký typ pohybu jde? Dopočítejte z kinematiky tohoto druhu pohybu čas, který potřebuje bedna na uražení dráhy s.
Celkové řešení
Na úvod si nakreslíme obrázek a znázorníme síly působící v naší situaci:
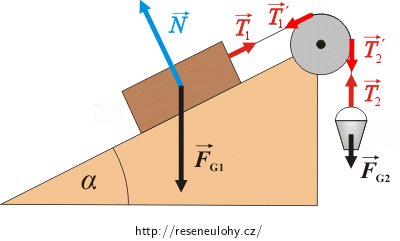
Pro velikosti sil roztáčejících kladku platí:
\[T'_1\,=\,T_1,\] \[T'_2\,=\,T_2.\]Aby se kladka roztáčela, je ale zřejmé, že:
\[T_1\,\neq\,T_2.\]Pohybové rovnice pro bednu a kyblík budou téměř stejné jako v úloze Bedna na nakloněné rovině s kladkou, pouze namísto síly T v nich v případě bedny vystupuje síla T1 a v případě kyblíku síla T2:
\[m_1gsin{\alpha}\,-\,T_1\,=\,m_1a,\tag{1}\] \[T_2\,-\,m_2g\,=\,m_2a,\tag{2}\]kde a je zrychlení bedny (i kyblíku) a g tíhové zrychlení. Postup, kterým byly tyto dvě pohybové rovnice určeny, je stejný jako v úloze Bedna na nakloněné rovině s kladkou, proto již není rozepsán podrobně.
Protože ale uvažujeme rotační pohyb kladky (resp. její moment setrvačnosti), je třeba napsat ještě třetí pohybovou rovnici, právě pro kladku. Pohybová rovnice rotačního pohybu má pro případ rotace kolem pevné osy tento tvar:
\[\vec{M}\,=\,J\vec{\varepsilon},\tag{3}\]kde M je výsledný moment sil působících na předmět vzhledem k určitému bodu, J moment setrvačnosti rotujícího předmětu (kladky) vzhledem k ose procházející daným bodem a ε úhlové zrychlení. Tyto tři veličiny nyní musíme určit.
Pro výsledný moment sil roztáčejících kladku můžeme psát:
\[\vec{M}\,=\,\vec{R}{\times}\vec{T'_1}\,+\,\vec{R}{\times}\vec{T'_2},\tag{4}\]kde R je poloměr kladky. Abychom mohli přepsat rovnici (4) skalárně, určíme pomocí pravidla pravé ruky směr momentů sil T1', T2'. Podle tohoto pravidla moment síly T1' míří před nákresnu (stejně jako vektor úhlového zrychlení) a dle dohody jej budeme psát s kladným znaménkem, zatímco moment síly T2' míří za nákresnu a budeme jej tedy považovat za záporný. Skalární přepis rovnice (4) pak vypadá následovně:
\[M\,=\,RT'_1\,-\,RT'_2\,=\,R(T'_1\,-\,T'_2).\tag{5}\]Již v první nápovědě jsme zmínili, že velikosti čárkovaných a nečárkovaných sil se rovnají, takže lze psát pro velikosti nečárkovaných sil:
\[M\,=\,R(T_1\,-\,T_2).\tag{6}\]Kladka je dle zadání homogenní válec o poloměru R a její moment setrvačnosti J vzhledem k ose procházející jejím středem tedy snadno určíme jako:
\[J\,=\,\frac{1}{2}m_3R^2.\tag{7}\]Konečně úhlové zrychlení je možné vyjádřit pomocí „obyčejného“ zrychlení jako:
\[\varepsilon\,=\,\frac{a}{R},\tag{8}\]kde a je zrychlení bedny.
Dosazením vztahů (6) až (8) do skalární podoby rovnice (3) dostáváme rozepsanou pohybovou rovnici pro rotační pohyb ve tvaru:
\[(T_1\,-\,T_2)R\,=\,\frac{1}{2}m_3R^2\frac{a}{R},\tag{9}\] \[T_1\,-\,T_2\,=\,\frac{1}{2}m_3a.\tag{10}\]Sečtením rovnic (1), (2) a (10) dostáváme:
\[m_1g\sin{\alpha}\,-\,m_2g\,=\,m_1a\,+\,\frac{1}{2}m_3a\,+\,m_2a.\tag{11}\]Úpravou tedy získáme:
\[a\,=\,g\frac{m_1\sin{\alpha}\,-\,m_2}{m_1\,+\,m_2\,+\,\frac{m_3}{2}}.\tag{12}\]Zrychlení bedny určené vztahem (12) je v čase konstantní, bedna se tedy pohybuje rovnoměrně zrychleným pohybem. Pro jeho dráhu s platí:
\[s\,=\,\frac{1}{2}at^2\,\Rightarrow\,t\,=\,\sqrt{\frac{2s}{a}}.\tag{13}\]Dosazením zrychlení a ze vztahu (10) dostáváme pro hledaný čas t:
\[t\,=\,\sqrt{\frac{2s}{a}}\,=\,\sqrt{\frac{2s}{g}\frac{m_1\,+\,m_2\,+\,\frac{m_3}{2}}{m_1\sin{\alpha}\,-\,m_2}}.\tag{14}\]Odpověď
Pro hledaný čas t, za kterou bedna urazí po nakloněné rovině dráhu s, platí:
\[t\,=\,\sqrt{\frac{2s}{g}\frac{m_1\,+\,m_2\,+\,\frac{m_3}{2}}{m_1\sin{\alpha}\,-\,m_2}}.\]



