Výtah
Úloha číslo: 136
Na obrázku je zakreslena časová závislost x(t) polohy kabiny výtahu.
a) Popište slovně pohyb kabiny.
b) Nakreslete závislost souřadnice rychlosti kabiny na čase.
c) Nakreslete závislost souřadnice zrychlení kabiny na čase.
d) U stropu kabiny visí pružina a na ní kulička. Popište chování pružiny během pohybu výtahu.
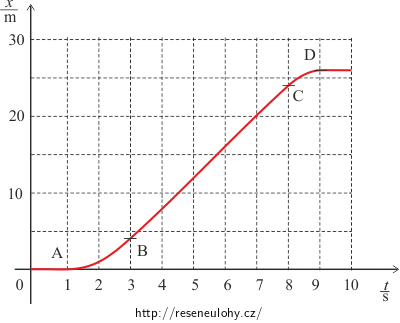
Bod A: poloha x = 0 m v čase t = 1 s
Bod B: poloha x = 4 m v čase t = 3 s
Bod C: poloha x = 24 m v čase t = 8 s
Bod D: poloha x = 26 m v čase t = 9 s
Nápověda 1 pro a): Popis pohybu
Rozdělte si pohyb kabiny výtahu na dílčí úseky mezi počátkem a bodem A, bodem A a bodem B, bodem B a bodem C, bodem C a bodem D a mezi bodem D a koncem. O jaké typy pohybu se v těchto úsecích jedná, zjistíte podle tvaru křivek odpovídajících závislosti x-ové souřadnice výtahu na čase.
Nápověda 2 pro b): Souřadnice rychlosti
Z předchozí části víte, o jaký typ pohybu v jednotlivých úsecích jde, takže již máte představu o tom, zda se velikost rychlosti kabiny výtahu mění a jak či zda se nemění.
Pro pohyb kabiny před bodem A a za bodem D je určení velikosti rychlosti kabiny snadné.
Mezi body A a B a mezi body C a D se výtah pohybuje rovnoměrně zrychleným (resp. zpomaleným) pohybem. Víte také pro oba případy, jaká je počáteční a konečná hodnota rychlosti. Její průběh do grafu již snadno zakreslíte.
Víte, že mezi body B a C se jedná o pohyb rovnoměrný přímočarý. Velikost rychlosti kabiny výtahu určíte z grafu ze zadání úlohy.
Komentář
Zamyslete se, zda by bylo možné opačně z grafu vx(t) určit průběh polohy x(t).
Řešení této úlohy není jednoznačné. Graf funkce vx(t) dává totiž informaci pouze o změnách polohy, nikoli o poloze samotné. Z grafu určíme změnu polohy v libovolném časovém intervalu jako
\[\int_\mathrm{t_1}^\mathrm{t_2}{v_\mathrm{x}(t)}\,,\]což odpovídá obsahu plochy pod křivkou v grafu vx(t) omezenou počátečním a koncovým bodem časového intervalu. K tomu, abychom určili, jaká byla poloha na začátku a na konci tohoto intervalu, ale potřebujeme další údaj, např. polohu v čase t = 0 s.
Nápověda 3 pro c): Souřadnice zrychlení
Víte již, jak se mění s časem souřadnice rychlosti výtahu.
Uvědomte si, jaké bude zrychlení v úsecích, kde se rychlost nemění.
V úsecích AB, resp. CD, rychlost lineárně narůstá, resp. klesá, velikost zrychlení určíte z grafu vx(t). Uvědomte si, jaký směr bude mít zrychlení v těchto úsecích.
Nápověda 4 pro d): Pružina s kuličkou
Uvědomte si, jaké síly působí na kuličku (z pohledu pozorovatele, který zůstane stát v přízemí) a co platí pro jejich výslednici v jednotlivých úsecích. Jak souvisí výsledná síla se zrychlením, říká 2. Newtonův zákon.
CELKOVÉ ŘEŠENÍ
a)
Mezi počátkem a bodem A se souřadnice výtahu nemění (je nulová). Kabina je tedy v klidu, stojí v dolním patře.
Mezi body A a B má závislost souřadnice na čase tvar paraboly, souřadnice kvadraticky roste. Výtah se pohybuje rovnoměrně zrychleným pohybem nahoru.
V úseku BC je grafem závislosti x-ové souřadnice na čase přímka, výtah se pohybuje konstantní rychlostí, kterou dosáhl v bodě B.
V úseku CD je grafem opět část paraboly, souřadnice sice narůstá, ale čím dál tím méně. Jde o rovnoměrně zpomalený pohyb, kabina brzdí až do zastavení.
Od bodu D se souřadnice nemění. Kabina je v klidu, stojí.
b)
Platí, že vx(t) je derivací funkce x(t), tj.
\[v_\mathrm{x}(t)=\frac{\mathrm{d}x}{\mathrm{d}t}\,.\]Úseky grafu před bodem A a za bodem D odpovídají situaci, kdy je kabina v klidu. Grafem funkce x(t) v těchto úsecích jsou přímky rovnoběžné s časovou osou. Směrnice tečen, a tedy i rychlost kabiny, je nulová.
V úseku mezi body B a C se kabina pohybuje konstantní rychlostí, kterou určíme jako směrnici přímky BC:
\[v_\mathrm{x}\,=\,\frac{\mathrm{\Delta}x}{\mathrm{\Delta}t}\,=\,\frac{(24-4)\,\mathrm{m}}{(8-3)\,\mathrm{s}}\,=\,4\,\mathrm{m\cdot s^{-1}}\,.\]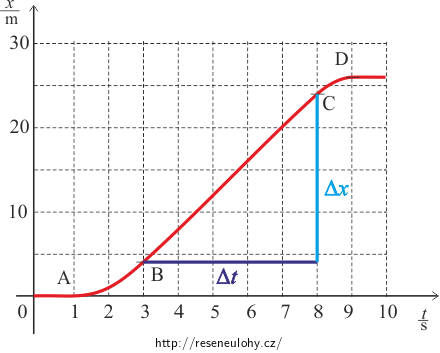
Bod A: poloha x = 0 m v čase t = 1 s
Bod B: poloha x = 4 m v čase t = 3 s
Bod C: poloha x = 24 m v čase t = 8 s
Bod D: poloha x = 26 m v čase t = 9 s
Při rozjezdu (úsek AB) a opětovném zastavení (úsek CD), tj. v časových intervalech od 1 s do 3 s a od 8 s do 9 s, se rychlost kabiny mění. Předpokládáme-li, že se výtah rozjíždí a brzdí rovnoměrně, bude závislost rychlosti na čase lineární (úsečky AB a CD).
Závislost rychlosti kabiny na čase je znázorněna v následujícím grafu:
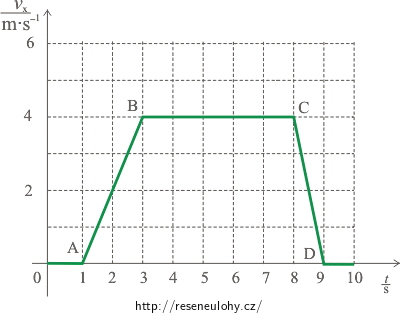
c)
Platí, že ax(t) je derivací funkce vx(t), tj.
\[a_\mathrm{x}(t)\,=\,\frac{\mathrm{d}v_\mathrm{x}}{\mathrm{d}t}\,.\]Úseky grafu před bodem A a za bodem D odpovídají situaci, kdy je kabina v klidu, má tedy nulové zrychlení.
Mezi body B a C je opět zrychlení nulové, protože kabina se pohybuje konstantní rychlostí.
Mezi body A a B rychlost lineárně narůstá, zrychlení bude tedy konstantní, bude kladné a jeho velikost určíme z grafu vx(t) jako směrnici přímky AB:
\[a_\mathrm{AB}\,=\,\frac{\mathrm{\Delta}v_\mathrm{AB}}{\mathrm{\Delta}t_\mathrm{AB}}\,=\,\frac{(4-0)\,\mathrm{m}}{(3-1)\,\mathrm{s^2}}\,=\, 2\,\mathrm{m \cdot s^{-2}}\,.\]Mezi body C a D rychlost lineárně klesá, zrychlení bude tedy konstantní, bude záporné a jeho velikost určíme z grafu vx(t) jako směrnici přímky CD:
\[a_\mathrm{CD}\,=\,\frac{\mathrm{\Delta}v_\mathrm{CD}}{\mathrm{\Delta}t_\mathrm{CD}}\,=\,\frac{(0-4)\,\mathrm{m}}{(9-8)\,\mathrm{s^2}}\,=\, -4\,\mathrm{m \cdot s^{-2}}\,.\]Závislost souřadnice zrychlení kabiny na čase je znázorněna v následujícím grafu:
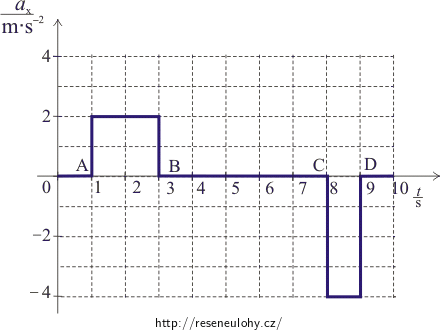
d)
Na kuličku působí Země gravitační silou a pružina, na které je zavěšena.
V úsecích před bodem A, BC a za bodem D, kde je zrychlení kabiny nulové, jsou tyto dvě síly v rovnováze, jejich výslednice je nulová.
V úseku AB musí pružina zatáhnout o něco více, aby udělila kuličce zrychlení směrem vzhůru – pružina se protáhne.
Naopak v úseku CD, kdy výtah zpomaluje, směřuje zrychlení dolů proti směru pohybu. Pružina musí tahat za kuličku méně než v klidovém stavu (nebo při rovnoměrném přímočarém pohybu), aby výslednice sil směřovala dolů – pružina se zkrátí.
Odpověď
a) Kabina nejprve stojí v dolním patře, je tedy v klidu — tomu odpovídá v grafu křivka mezi počátkem a bodem A. Pak se rozjíždí směrem vzhůru (kladný směr souřadnicové osy), pohybuje se rovnoměrně zrychleným pohybem, až dosáhne určité rychlosti – tomu odpovídá v grafu křivka mezi body A a B. Touto konstantní rychlostí se kabina určitou dobu pohybuje (rovnoměrný přímočarý pohyb) — tomu odpovídá v grafu křivka mezi body B a C. Nakonec začne kabina brzdit, pohybuje se rovnoměrně zpomaleným pohybem, až se zastaví — tomu odpovídá v grafu křivka mezi body C a D. Křivka od bodu D opět odpovídá tomu, že je kabina v klidu.
b) Závislost souřadnice rychlosti kabiny na čase je znázorněna v následujícím grafu:

c) Závislost souřadnice zrychlení kabiny na čase je znázorněna v následujícím grafu:

d) V případech, kdy je kabina v klidu (úseky grafu před bodem A a za bodem D) nebo se pohybuje rovnoměrným přímočarým pohybem (úsek grafu mezi body B a C) je protažení pružiny stále stejné. Při rozjíždění kabiny (úsek grafu mezi body A a B) dochází oproti klidovému stavu kabiny k delšímu protažení pružiny. Naopak při zpomalování kabiny (úsek grafu mezi body C a D) dochází oproti klidovému stavu kabiny ke zkrácení pružiny.





