Indiana Jones a kamenná koule
Úloha číslo: 604
V památné scéně z filmu Indiana Jones a Dobyvatelé ztracené archy utíká Indy chodbou před ohromnou kamennou koulí.
a) Podívejte se na obrázek a odhadněte hmotnost koule, je-li její hustota přibližně 2500 kg·m−3.
b) Jaká je celková kinetická energie koule, pronásledující známého archeologa, pohybuje-li se bez podkluzování a její hmotný střed má rychlost 4 m·s−1?
c) Koule byla nejspíše v pasti udržována v klidu a svou energii získala po uvolnění pouhým kutálením se z výšky. Z jaké minimální výšky se musela kamenná koule svalit, aby zmíněnou kinetickou energii získala?
Uvažujte nejprve, že se koule valí přímo po podlaze chodby (A). Pak úkoly řešte pro situaci, kdy se koule valí ve žlabu, jak ukazuje obrázek (B). Předpokládejte, že koule se dotýká žlabu v kolmé vzdálenosti \(\frac{2}{3}r\) od středu.

Zápis
ρ = 2 500 kg·m-3 hustota koule v = 4 m·s-1 rychlost hmotného středu koule r = ? poloměr koule m = ? hmotnost koule Ek = ? kinetická energie koule h = ? počáteční výška Nápověda 1 a): Hmotnost koule
Odhadněte poloměr koule a spočtěte její hmotnost.
Nápověda 2 b) A,B – kinetická energie koule
Kinetická energie koule se skládá ze dvou složek, neboť koule provádí pohyb posuvný i otáčivý.Nápověda 3 b) A – kinetická energie koule
Jaký je vztah mezi rychlostí hmotného středu koule v a úhlovou rychlostí otáčení ω v případě, že se koule valí po podlaze chodby?
Čemu je roven moment setrvačnosti koule J?
Nápověda 3 b) B – kinetická energie koule
Jaký je vztah mezi rychlostí hmotného středu koule v a úhlovou rychlostí otáčení ω v případě, že se koule valí ve žlabu? Co se změní oproti předchozímu případu?
Nápověda 4 c) A,B – minimální výška
Předpokládejme, že se veškerá počáteční potenciální energie tíhová koule \(E_\mathrm{p0}\) beze ztrát proměnila v energii kinetickou. Co z toho vyplývá pro počáteční výšku koule?
Komentář
Pro srovnání, 50 g kokosové tyčinky má energetickou hodnotu téměř 1000 kJ.
Celkové řešení
hustota koule ... ρ = 2 500 kg·m-3
rychlost hmotného středu koule ... v = 4 m·s-1
poloměr koule ... r
hmotnost koule ... m
kinetická energie koule ... \(E_\mathrm{k}\)
počáteční výška ... h
a) Odhad hmotnosti koule:
Průměr koule bude podle obrázku odpovídat výšce Indyho. Odhadněmě ho na 2 m. Poloměr koule pak bude roven 1 m.
Hmotnost koule je rovna:
\[m = \rho V = \rho \frac{4}{3}\pi r^3\,.\]Číselně:
\[m = 2 500 \cdot \frac{4}{3}\cdot \pi \cdot 1^3 \, \mathrm{kg} \,\dot= 10{,}5 \, \mathrm{t}\,.\]b) Výpočet kinetické energie:
Kinetická energie valící se koule je součtem energie pohybu translačního a pohybu rotačního.
Energie translačního pohybu je:
\[E_\mathrm{t}=\frac{1}{2}mv^2\,.\]Energie pohybu rotačního je:
\[E_\mathrm{r}=\frac{1}{2}J\omega^2,\]kde J je moment setrvačnosti koule vzhledem k ose jdoucí středem, ω je úhlová rychlost otáčení.
Kinetická energie koule je:
\[E_\mathrm{k} = E_\mathrm{t} + E\mathrm{r} = \frac{1}{2}mv^2 + \frac{1}{2}J\omega^2\,.\tag{1}\]A. Koule se valí po podlaze chodby:
Koule pronásledující dobrodruha nepodkluzuje, takže platí vztah:
\[v=\omega r\,.\]Pro moment setrvačnosti koule vzhledem k ose jdoucí jejím středem platí vztah:
\[J = \frac{2}{5}mr^2\,.\]Dosazením do vztahu (1) dostáváme:
\[E_\mathrm{k}=\frac{1}{2}mv^2+ \frac{1}{2}J\omega^2 = \frac{1}{2}mv^2+\frac{1}{2}(\frac{2}{5}mr^2)(\frac{v}{r})^2=\frac{1}{2}mv^2 + \frac{1}{5}mv^2\,,\] \[E_\mathrm{k} = \frac{7}{10}mv^2\,.\tag{2}\]Číselně:
\[E_\mathrm{k}=\frac{7}{10}\cdot 10500{\cdot} 4^2 \,\mathrm J = 117 600\,\mathrm J\,,\] \[E_\mathrm{k} \dot{=} 118 \,\mathrm kJ\,.\]B. Koule se valí ve žlabu:
Pro úhlovou rychlost otáčení koule platí:
\[\omega = \frac{v}{r_1} (=\frac{v_r}{r})\,.\]Rychlost hmotného středu koule je rovna:
\[v = \omega r_1\,.\]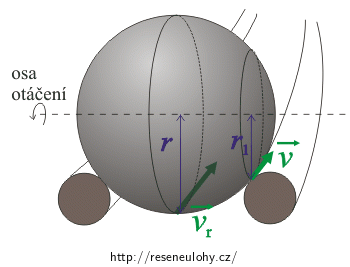
Pro výpočet kinetické energie využijeme opět vztah (1):
\[E_\mathrm{k}=\frac{1}{2}mv^2+ \frac{1}{2}J\omega^2 = \frac{1}{2}mv^2+\frac{1}{2}(\frac{2}{5}mr^2)(\frac{v}{r_1})^2=\frac{1}{2}mv^2 (1+ \frac{2}{5}\frac{r^2}{r_1^2})\,.\]Dosadíme za \(r_1 = \frac{2}{3}r\):
\[E_\mathrm{k} = \frac{1}{2}mv^2 (1+\frac{9}{10})\,,\] \[E_\mathrm{k} = \frac{19}{20}mv^2\,.\tag{3}\]Číselně:
\[E_\mathrm{k}=\frac{19}{20}\cdot 10500{\cdot} 4^2 \,\mathrm J = 159 600\,\mathrm J\,,\] \[E_\mathrm{k} \dot{=} 160\,\mathrm kJ\,.\]c) Výpočet minimální výšky:
Pokud by došlo k bezeztrátové přeměně potenciální energie tíhové v kinetickou, musí platit:
\[E_\mathrm{k} = E_\mathrm{p0}\,.\] Pro potenciální energii tíhovou platí: \[E_\mathrm{p0} = mgh\,.\]Za Ek dosadíme ze vztahu (2) pro případ valení po podlaze chodby, resp. ze vztahu (3) v případě valení ve žlabu.
A. Valení po podlaze chodby:
\[\frac{7}{10}mv^2=mgh\,.\]Všimněme si, že na hmotnosti koule výsledek záviset nebude:
\[\frac{7}{10}v^2=gh\,,\] \[h=\frac{7}{10}\frac{v^2}{g}\,.\]Číselně:
\[h=\frac{7}{10}\cdot\frac{4^2}{9{,}81}\,\mathrm m \dot{=} 1{,}1 \,\mathrm m\,.\]B. Valení ve žlabu:
\[\frac{19}{20}mv^2=mgh\,.\]Na hmotnosti koule výsledek opět nezávisí:
\[\frac{19}{20}v^2=gh\,,\] \[h=\frac{19}{20}\frac{v^2}{g}\,.\]Číselně:
\[h=\frac{19}{20}\cdot\frac{4^2}{9{,}81}\,\mathrm m \dot{=} 1{,}5 \,\mathrm m\,.\]Poznámka:
Výškou se rozumí, o kolik koule spadne ve svislém směru.
Odpověď
a) Koule pronásledující Indyho má přibližně hmotnost 10,5 t.
b) Koule pronásledující Indyho má kinetickou energii:
A. V případě valení po dně chodby:
\[E_\mathrm{k} = \frac{7}{10}mv^2 \dot{=} 118 \,\mathrm kJ\,.\]B. V případě valení ve žlabu:
\[E_\mathrm{k} = \frac{19}{20}mv^2 \dot{=} 160\,\mathrm kJ\,.\]c) Koule mohla získat svou energii sjetím z výšky alespoň:
A. V případě valení po dně chodby:
\[h=\frac{7}{10}\frac{v^2}{g}\dot{=} 1{,}1 \,\mathrm m\,.\]B. V případě valení ve žlabu:
\[h=\frac{19}{20}\frac{v^2}{g}\dot{=} 1{,}5 \,\mathrm m\,.\]



