Pohyb kola
Úloha číslo: 118
Kolo o poloměru 5 m se rovnoměrně roztáčí. Velikost rychlosti značky na obvodu kola závisí na čase vztahem v(t) = 0,5 m·s-2·t. Vypočtěte velikost celkového zrychlení pohybu značky a úhel, který svírají vektory rychlosti a celkového zrychlení v časech 1 s a 4 s.
Zápis
R = 5 m poloměr kola v(t) = a·t; a = 0,5 m·s-2 časová závislost velikosti rychlosti značky ac = ? (m·s-2) velikost celkového zrychlení pohybu značky β = ? (°) úhel, který svírají vektory rychlosti a celkového zrychlení Nápověda 1: Rychlost, celkové zrychlení
Nakreslete si obrázek a do něj zakreslete, kam míří vektor rychlosti a celkového zrychlení bodu (značky). Uvědomte si, o jaký pohyb se jedná a jaké složky má celkové zrychlení.
Nápověda 2: Tečné, normálové zrychlení a jejich velikost
Jak velké je tečné a jak velké je normálové zrychlení? Velikost celkového zrychlení pak jistě snadno určíte.
Nápověda 3: Úhel beta
Úhel β snadno určíte pomocí obrázku z první nápovědy a tečného a normálového zrychlení.
CELKOVÉ ŘEŠENÍ
Výpočet velikosti celkového zrychlení:
Pro velikost tečného zrychlení at platí:
\[a_\mathrm{t}\,=\,\frac{\mathrm{d}v}{\mathrm{d}t}\,=\, \frac{\mathrm{d}\left(at\right)}{\mathrm{d}t}\,=\, a\,.\]Pro velikost normálového zrychlení an platí:
\[a_\mathrm{n}\,=\,\frac{v^{2}}{R}\,=\,\frac{a^{2}t^{2}}{R}\,.\]Velikost celkového zrychlení ac vypočteme z velikostí tečného zrychlení at a normálového zrychlení an:
\[a_\mathrm{c}\,=\,\sqrt{a_\mathrm{t}^{2}+a_\mathrm{n}^{2}}\,,\] \[a_\mathrm{c}\left(t\right)\,=\,\sqrt{a^{2}+\frac{a^{4}t^{4}}{R^{2}}}\,=\,a\sqrt{1+\frac{a^{2}t^{4}}{R^{2}}}\,.\]Číselně:
\[a_\mathrm{c}\left(1\right)\,=\,0{,}5\sqrt{1+\frac{0{,}5^{2}\cdot 1^{4}}{5^{2}}}\,\mathrm{m \cdot s^{-2}} \,=\,0{,}5\,\mathrm{m \cdot s^{-2}}\,,\] \[a_\mathrm{c}\left(4\right)\,=\, 0{,}5\sqrt{1+\frac{0{,}5^{2}\cdot 4^{4}}{5^{2}}}\,\mathrm{m \cdot s^{-2}}\,=\, 0{,}94\,\mathrm{m \cdot s^{-2}}\,.\]Výpočet úhlu β:
Obrázek situace:
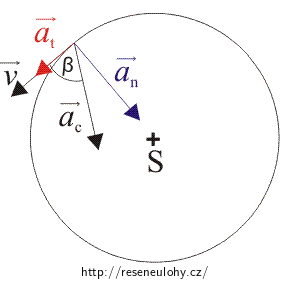
Úhel β mezi vektory rychlosti a celkového zrychlení je zároveň úhlem mezi tečným a celkovým zrychlením. Podle obrázku potom platí:
\[tg\beta\,=\,\frac{a_\mathrm{n}}{a_\mathrm{t}}\,=\,\frac{a^{2}t^{2}}{Ra}\,=\,\frac{at^{2}}{R}\,,\] \[\beta\left(t\right)\,=\,arctg\frac{at^{2}}{R}\,,\] \[\beta\left(1\right)\,=\,arctg\frac{0{,}5{\cdot} 1^{2}}{5}\,=\,5{,}7\,^{\circ}\,,\] \[\beta\left(4\right)\,=\,arctg\frac{0{,}5{\cdot} 4^{2}}{5}\,=\,58\,^{\circ}\,.\]Odpověď
Velikost celkového zrychlení ac je:
\[a_\mathrm{c}(t)= a\sqrt{1+\frac{a^{2}t^{4}}{R^{2}}}\,.\]Číselně:
\[a_\mathrm{c}(1)= 0{,}5\,\mathrm{m \cdot s^{-2}}\,,\] \[a_\mathrm{c}(4)= 0{,}94\,\mathrm{m \cdot s^{-2}}\,.\]Úhel β je:
\[\beta(t)=arctg\frac{at^{2}}{R}\,.\]Úhel β v okamžiku t1 = 1 s je:
\[\beta(1)= 5{,}7^{\circ}\,.\]Úhel β v okamžiku t2 = 4 s je:
\[\beta(4)= 58^{\circ}\,.\]



