Pevná kladka
Úloha číslo: 99
Na pevné kladce visí závaží o hmotnosti 0,55 kg a kbelík o hmotnosti 0,45 kg. Určete zrychlení soustavy a sílu, kterou působí kladka na osu. Hmotnost kladky i provázku zanedbejte, tření neuvažujte.
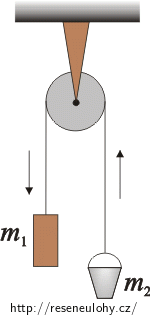
Zápis
m1 = 0,55 kg hmotnost závaží m2 = 0,45 kg hmotnost kbelíku a = ? m·s−2 zrychlení soustavy Fk = ? N síla, kterou působí kladka na osu Nápověda 1 – pohybové rovnice, výpočet zrychlení
Nakreslete si obrázek a v něm vyznačte všechny síly, které působí na závaží a na kbelík. Napište pro závaží a kbelík jejich pohybové rovnice. Zaveďte si souřadný systém.
Nápověda 2 – výpočet síly působící na osu kladky
Síla, kterou působí kladka na osu, je podle 3. Newtonova zákona stejně velká jako síla, kterou působí osa na kladku. Nakreslete si všechny síly, které působí na kladku, a uvědomte si, jaká je jejich výslednice.
CELKOVÉ ŘEŠENÍ
Do obrázku vyznačíme všechny síly působící na kbelík a závaží a napíšeme pro ně pohybové rovnice.
Síly působící na závaží:
Závaží m1:
\(\vec{F}_\mathrm{G1}\)…síla tíhová
\(\vec{T}_1\)…tahová síla provázku
Závaží m2:
\(\vec{F}_\mathrm{G2}\)…síla tíhová
\(\vec{T}_2\)…tahová síla provázku
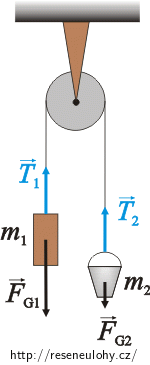
Pohybové rovnice:
Závaží m1:
\[\vec{F}_\mathrm{G1}+\vec{T}_1\,=\,m_1\vec{a}.\]Kbelík m2:
\[\vec{F}_\mathrm{G2}+\vec{T}_2\,=\,m_2\vec{a}.\]Závaží a kbelík se pohybují se stejně velkým zrychlením opačné orientace.
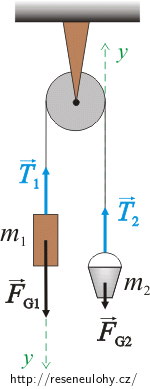
Zvolme si osu y, jak je vyznačeno na obrázku. Přepíšeme rovnice skalárně:
\[F_\mathrm{G1} - T_1 \,=\, m_\mathrm{1a},\tag{1}\] \[T_2 - F_\mathrm{G2} \,=\, m_\mathrm{2a}.\tag{2}\]Jelikož hmotnost kladky zanedbáváme, nemá žádný moment setrvačnosti a neovlivňuje provázkové síly. Závaží m1 působí prostřednictvím provázku na kbelík m2, a kbelík m2 zase naopak na závaží m1. Podle 3. Newtonova zákona platí pro velikosti provázkových sil:
\[|\vec{T}_1| \,=\, |\vec{T}_2| \,=\, |\vec{T}|\,.\]Dosadíme do rovnic (1) a (2):
\[m_1g - T \,=\, m_1a,\tag{3}\] \[T - m_2g \,=\, m_2a.\tag{4}\]Výpočet zrychlení:
Součtem rovnic (3) a (4) dostáváme:
\[m_1g - m_2g \,=\, m_1a+m_2a,\] \[(m_1 - m_2)g \,=\, (m_1+m_2)a,\] \[a\,=\,\frac{(m_1 - m_2)g}{m_1+m_2}.\tag{5}\]Dosadíme a spočteme zrychlení číselně:
\[a\,=\,\left(\frac{\left(0{,}55\,-\,0{,}45\right)9{,}81}{0{,}55+0{,}45}\right)\,\mathrm{m\cdot s^{-2}}\,\dot=\,0{,}98\,\mathrm{m\cdot s^{-2}}\,.\]Výpočet síly působící na osu kladky:
Na kladku působí po stranách tahové síly provázku \(\vec{T}_1^\prime\) a \(\vec{T}_2^\prime\) a dále osa, na které je kladka upevněna, silou \(\vec{F}_\mathrm{k}\) (hmotnost kladky a tedy i tíhovou sílu působící na kladku neuvažujeme).
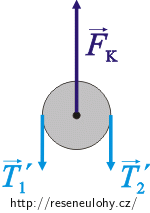
Posuvné zrychlení kladky je nulové, takže je nulová i výslednice sil na ni působících:
\[\vec{T}_1^\prime\,+\,\vec{T}_2^\prime\,+\,\vec{F}_\mathrm{k}\,=\,0\,.\tag{6}\]Jelikož hmotnost kladky zanedbáváme, nemá žádný moment setrvačnosti a neovlivňuje provázkové síly. Pro provázkové síly podle 3. Newtonova zákona platí:
\[|\vec{T}_1^\prime| \,=\, |\vec{T}_2^\prime| \,=\, |\vec{T}|\,.\]Rovnici (6) přepíšeme skalárně:
\[2T\,-\,F_\mathrm{k}\,=\,0,\] \[2T\,=\,F_\mathrm{k}.\tag{7}\]Tahovou sílu můžeme vyjádřit buďto z rovnice (3), nebo (4):
\[F_\mathrm{k}\,=\,2m_2\left(a+g\right)\,=\,2m_1\left(g-a\right)\,.\tag{8}\]Dosadíme do rovnice (8) číselně:
\[F_\mathrm{k}\,=\,2\,\cdot\,0{,}45\left(9{,}81\,+\,0{,}98\right)\,\mathrm{N}\,=\,2\,\cdot\,0{,}55\left(9{,}81\,-\,0{,}98\right)\,\mathrm{N},\] \[F_\mathrm{k}\,=\,0{,}9\,\cdot10{,}79\,\mathrm{N}\,=\,1{,}1\,\cdot8{,}83\,\mathrm{N},\] \[F_\mathrm{k}\,\dot=\,9{,}71\,\mathrm{N}.\]CELKOVÁ ODPOVĚĎ
Zrychlení soustavy je \(a\,\dot=\,0{,}98\,\mathrm{m\cdot s^{-2}}\).
Síla, kterou působí kladka na osu, je \(F_\mathrm{k}\,\dot=\,9{,}71\,\mathrm{N}\).






