Sbírka řešených úloh

Rozklad sil

Úloha číslo: 1134

Závaží, na které působí tíhová síla F_G, je upevněno na dvou tyčích K a L (viz obr. 1).

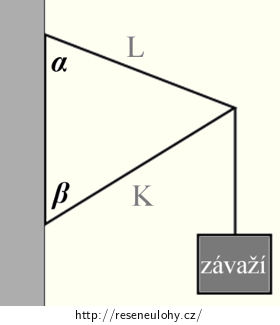
Obrázek 1

Obecně vyjádřete velikost sil přenášených tyčemi K a L.

• Nápověda 1

  Které síly působí v místě styku tyčí na závěs a jaký mají směr? Zakreslete je do obrázku. Jaká je výslednice těchto sil?

• Řešení nápovědy 1

  V místě styku tyčí působí na závěs tyto síly (viz obr. 2):

  • tlaková síla K ve směru tyče K,
  • tažná síla L ve směru tyče L,
  • směrem svisle dolů táhne závaží svou tíhou G = F_G.

  

  Protože závěs je vzhledem k nosné konstrukci v klidu, musí být výslednice těchto sil nulová:

  \[\vec{F}_\mathrm{G}\,+\,\vec{K}\,+\,\vec{L}\,=\,\vec{o}.\]

• Nápověda 2

  Sestrojte si do obrázku 2 výslednici sil K a L. Její velikost znáte. Vyznačte, kde všude jsou ve vzniklém rovnoběžníku sil úhly α a β. Zvolte jeden z trojúhelníků, ve kterém znáte všechny tři úhly a jednu stranu. Umíte na tento trojúhelník (obecně ne pravoúhlý) aplikovat nějaké matematické pravidlo a vyjádřit velikosti zbývajících dvou stran odpovídajících velikostem sil K a L?

• Řešení nápovědy 2

  Síly F_G, K a L vymezují trojúhelník ABC, vyznačený v obrázku 3. V tomto trojúhelníku známe všechny úhly i stranu AB a lze pro něj tedy napsat sinovou větu.

  

• Nápověda 3

  Napište sinovou větu pro trojúhelník ABC a vyjádřete z ní velikosti hledaných sil K a L.

• Řešení nápovědy 3

  Sinová věta pro trojúhelník ABC má tvar:

  \[\frac{K}{\sin{\alpha}}\,=\,\frac{L}{\sin{\beta}}\,=\,\frac{F_\mathrm{G}}{\sin({\pi\,-\,(\alpha\,+\,\beta))}}.\tag{1}\]

  Z vlastností funkce sinus víme:

  \[\sin{(\pi\,-\,(\alpha\,+\,\beta))}\,=\,\sin(\alpha\,+\,\beta).\tag{2}\]

  Ze vztahů (1) a (2) tedy plyne:

  \[K\,=\,\frac{F_\mathrm{G}\sin{\alpha}}{\sin(\alpha\,+\,\beta)},\] \[L\,=\,\frac{F_\mathrm{G}\sin{\beta}}{\sin(\alpha\,+\,\beta)}.\]

• Celkové řešení

  Na závěs působí v místě styku tyčí tyto síly (viz obr. 2):

  • tlaková síla K ve směru tyče K,
  • tažná síla L ve směru tyče L,
  • směrem svisle dolů táhne závaží svou tíhou G = F_G.

   

  

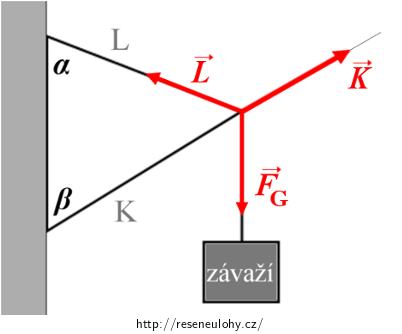
  Protože závěs je vzhledem k nosné konstrukci v klidu, musí být výslednice výše těchto sil nulová:

  \[\vec{F}_\mathrm{G}\,+\,\vec{K}\,+\,\vec{L}\,=\,\vec{o}.\]

  Síly F_G, K a L vymezují trojúhelník ABC, vyznačený v obrázku 3.

  

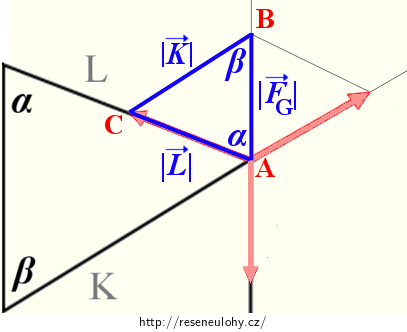
  V tomto trojúhelníku známe všechny úhly i stranu AB a lze pro něj tedy napsat sinovou větu:

  \[\frac{K}{\sin{\alpha}}\,=\,\frac{L}{\sin{\beta}}\,=\,\frac{F_\mathrm{G}}{\sin({\pi\,-\,(\alpha\,+\,\beta))}}.\tag{1}\]

  Z vlastností funkce sinus víme:

  \[\sin{(\pi\,-\,(\alpha\,+\,\beta))}\,=\,\sin(\alpha\,+\,\beta).\tag{2}\]

  Ze vztahů (1) a (2) tedy plyne:

  \[K\,=\,\frac{F_\mathrm{G}\sin{\alpha}}{\sin(\alpha\,+\,\beta)},\] \[L\,=\,\frac{F_\mathrm{G}\sin{\beta}}{\sin(\alpha\,+\,\beta)}.\]

• Odpověď

  Pro velikosti sil K a L platí:

  \[K\,=\,\frac{F_\mathrm{G}\sin{\alpha}}{\sin(\alpha\,+\,\beta)},\] \[K\,=\,\frac{F_\mathrm{G}\sin{\beta}}{\sin(\alpha\,+\,\beta)}.\]