Brouk na desce
Úloha číslo: 111
K popisu pohybu brouka lezoucího po dřevěné desce jsme si na desku nakreslili mřížku. Z mřížky jsme vyčetli, že se pohyboval po přímce dané rovnicí y = 2x + 3.
Napište parametrické rovnice pohybu brouka pro případ:
a) Brouk se pohyboval rovnoměrným přímočarým pohybem rychlostí o velikosti 2 cm·s-1 a v čase 0 s se nacházel v bodě o souřadnicích [0; 3] cm.
b) Brouk se pohyboval rovnoměrně zrychleným pohybem se zrychlením o velikosti 0,25 cm·s-2. V čase 0 s byla velikost počáteční rychlosti brouka 1,5 cm·s-1 a brouk se nacházel v bodě [0; 3] cm.
Poznámka: Parametrické rovnice by měly být zapsány ve tvaru např.:
\[y=1\,\mathrm{m}\,-\,2\,\mathrm{m\,s^{-1}}\,\cdot\,t\,.\]Pro zjednodušení zápisu jednotky ve vztazích nepíšeme.
Zápis
y = 2x+3 rovnice přímky, po které se pohyboval brouk [x, y] = [0, 3] cm souřadnice brouka v čase t = 0 s a) v = 2 cm·s-1 rychlost brouka při rovnoměrném přímočarém pohybu b) a = 0,25 cm·s-2 zrychlení brouka při rovnoměrně zrychleném přímočarém pohybu b) v0 = 1,5 cm·s-1 počáteční rychlost brouka v čase t = 0 s Nápověda 1 pro a): Grafické znázornění pohybu brouka
Zakreslete si danou přímku do grafu a vyznačte počáteční polohu brouka. Pak vyznačte, kde se bude brouk nacházet za okamžik t (pozor, jsou dvě možnosti).
Nápověda 2 pro a): Pohyb brouka ve směru os x a y
Varianta 1:
Jakou dráhu brouk za čas t ulezl? Jaká je jeho x-ová a y-ová souřadnice v čase t?
(Úhel, který svírá přímka s osou x, zjistíte z jejích průsečíků s osami x a y.)
Varianta 2:
Úlohu můžete řešit také tak, že si pohyb brouka rovnou rozložíte do směru osy x a y. Jakým pohybem se pohybuje ve směru osy x a jakou rychlostí? Jak se bude s časem měnit jeho x-ová souřadnice?
Jakým pohybem se pohybuje ve směru osy y a jakou rychlostí a jak se bude s časem měnit jeho y-ová souřadnice?
Nápověda 3 pro b): Pohyb brouka ve směru os x a y
Obdobně postupujte u řešení úkolu b). Rozložte si pohyb brouka do směru osy x a y. Jakým pohybem se pohybuje ve směru osy x a jakou počáteční rychlostí? Jaké bude jeho zrychlení ve směru osy x? Jak se bude s časem měnit jeho x-ová souřadnice?
Jakým pohybem se pohybuje ve směru osy y a jakou počáteční rychlostí? Jaké bude jeho zrychlení ve směru osy y? Jak se bude s časem měnit jeho y-ová souřadnice?
CELKOVÉ ŘEŠENÍ
Nakreslíme obrázek situace: (Kliknutím na obrázek si ho lze zvětšit.)
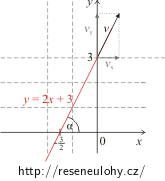
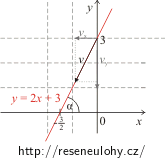
Obrázek 1: Obrázek 2: Brouk se vydá po přímce směrem doprava. Brouk se vydá po přímce směrem doleva. a)
Jedná se o pohyb rovnoměrný přímočarý s rychlostí o velikosti v = 2 cm·s-1.
Složka rychlosti ve směru osy x je rovna:
\[v_\mathrm{x}\,=\,v\cos\alpha\,.\]Souřadnice x se s časem bude měnit podle vztahu (brouk může lézt doprava nebo doleva):
\[x(t)\,=\,\pm{v_\mathrm{x}t}\,,\] \[x(t)\,=\, \pm (v\,\cos\alpha)t\,.\tag{1}\]Složka rychlosti ve směru osy y je rovna:
\[v_\mathrm{y}\,=\,v\,\sin\alpha\,.\]Souřadnice y se s časem bude měnit podle vztahu (brouk může lézt doprava nebo doleva):
\[y(t)\,=\,\pm{v_\mathrm{y}t}+3\,,\] \[y(t)\,=\, \pm (v\,\sin\alpha)t+3\,.\tag{2}\]Z obrázku 1, 2:
\[\cos\alpha\,=\,\frac{\frac{3}{2}}{\sqrt{3^{2}+(\frac{3}{2})^{2}}}\,=\,\frac{\sqrt{5}}{5}\,,\tag{3}\] \[\sin\alpha\,=\, \frac{3}{\sqrt{3^{2}+(\frac{3}{2})^{2}}}\,=\,\frac{2\sqrt{5}}{5}\,.\tag{4}\]Dosazením do vztahu (1) za v a cosα:
\[x(t)\,=\,\pm\frac{2\sqrt{5}}{5}t\,.\]Dosazením do vztahu (2) za v a sinα:
\[y(t)\,=\,\pm\frac{4\sqrt{5}}{5}t+3\,.\]b)
Jedná se o pohyb rovnoměrně zrychlený se zrychlením o velikosti a = 0,25 cm·s-2 a s počáteční rychlostí o velikosti v0 = 1,5 cm·s-1.
Složky počáteční rychlosti ve směru os x a y jsou:
\[v_\mathrm{0_x}\,=\,\pm{v_0}\cos\alpha\,,\] \[v_\mathrm{0_y}\,=\,\pm{v_0}\sin\alpha\,.\]Dosadíme za v0, cosα (viz vztah 3) a sinα (viz vztah 4):
\[v_\mathrm{0_x}\,=\,\pm1{,}5\frac{\sqrt{5}}{5}\,\mathrm{cm\,s^{-1}}\,=\,\pm\frac{3\sqrt{5}}{10}\,\mathrm{cm\,s^{-1}}\,,\] \[v_\mathrm{0_y}\,=\,\pm1{,}5\frac{2\sqrt{5}}{5}\,\mathrm{cm\,s^{-1}}=\pm\frac{3\sqrt{5}}{5}\,\mathrm{cm\,s^{-1}}\,.\]Složky zrychlení ve směru os x a y jsou:
\[a_\mathrm{x}\,=\,\pm{a}\cos\alpha\,,\] \[a_\mathrm{y}\,=\,\pm{a}\sin\alpha\,.\]Dosadíme za a, cosα (viz vztah 3) a sinα (viz vztah 4):
\[a_\mathrm{x}\,=\,\pm0{,}25\frac{\sqrt{5}}{5}\,\mathrm{cm\,s^{-2}}\,=\,\pm\frac{\sqrt{5}}{20}\,\mathrm{cm\,s^{-2}}\,,\] \[a_\mathrm{y}\,=\,\pm0{,}25\frac{2\sqrt{5}}{5}\,\mathrm{cm\,s^{-2}}\,=\,\pm\frac{\sqrt{5}}{10}\,\mathrm{cm\,s^{-2}}\,.\]Složky rychlosti se s časem budou měnit podle vztahů:
\[v_\mathrm{x} (t)\,=\, \int{a_\mathrm{x}(t)}dt \,=\, \pm(v_\mathrm{0_x}+a_\mathrm{x}t)\,,\] \[v_\mathrm{y} (t)\,=\, \int{a_\mathrm{y}(t)}dt \,=\, \pm(v_\mathrm{0_y}+a_\mathrm{y}t)\,.\]Pro souřadnice x a y pak platí:
\[x(t)\,=\,\int{v_\mathrm{x}(t)}dt \,=\, \pm{v_\mathrm{0_x}t}\pm\frac{1}{2}a_\mathrm{x}t^{2}+x_0\,,\] \[y(t)\,=\, \int{v_\mathrm{y}(t)}dt \,=\, \pm{v_\mathrm{0_y}t}\pm\frac{1}{2}a_\mathrm{y}t^{2}+y_0\,.\]Dosadíme číselně za v0x, v0y, ax, ay, x0, y0:
\[x(t)\,=\, \pm\frac{\sqrt{5}}{40}t^{2}\pm\frac{3\sqrt{5}}{10}t\,,\] \[y(t)\,=\, \pm\frac{\sqrt{5}}{20}t^{2}\pm\frac{3\sqrt{5}}{5}t+3\,. \]Odpověď
a) Parametrické rovnice pohybu brouka v případě, kdy se pohyboval rovnoměrně přímočaře, jsou:
\[x(t)\,=\, \pm (v\cos\alpha)t \,=\,\pm\frac{2\sqrt{5}}{5}t\,,\] \[y(t)\,=\, \pm (v\sin\alpha)t+3 \,=\,\pm\frac{4\sqrt{5}}{5}t+3\,.\]b) Parametrické rovnice pohybu brouka v případě, kdy se pohyboval rovnoměrně zrychleně, jsou:
\[x(t)\,=\,\pm{v_\mathrm{0_x}t}\pm\frac{1}{2}a_\mathrm{x}t^{2}+x_0\,=\,\pm\frac{\sqrt{5}}{40}t^{2}\pm\frac{3\sqrt{5}}{10}t\,,\] \[y(t)\,=\, \pm{v_\mathrm{0_y}t}\pm\frac{1}{2}a_\mathrm{y}t^{2}+y_0\,=\,\pm\frac{\sqrt{5}}{20}t^{2}\pm\frac{3\sqrt{5}}{5}t+3\,. \]