Deformace kvádru
Úloha číslo: 2156
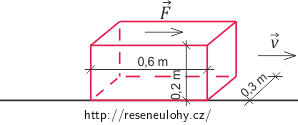
Ocelový kvádr s podstavou o rozměrech 0,3 m a 0,6 m a výškou 0,2 m se pohybuje rovnoměrně přímočaře po vodorovné podlaze ve směru svého největšího rozměru. Pohyb se děje vlivem tečné síly působící na horní stěnu kvádru. Modul pružnosti ve smyku je 80 GPa, a hustota oceli je 8000 kg·m-3. Určete úhel smyku, o který se kvádr deformuje, jestliže při větší výšce kvádru by k deformaci již nedošlo a kvádr by se překlopil.
Zápis
a = 0,6 m rozměr podstavy kvádru b = 0,3 m rozměr podstavy kvádru c = 0,2 m výška kvádru G = 80 GPa modul pružnosti ve smyku ρ = 8000 kg·m-3 objemová hustota oceli α = ? úhel smyku Rozbor
Nejprve je třeba rozmyslet, jaké síly na kvádr působí, jaké jsou jejich účinky a jaká je hraniční podmínka, aby došlo ještě k deformaci.
Na kvádr působí tíhová síla, její působiště je v těžišti kvádru. Dále tlačí do kvádru odspodu podložka. Pokud by jiné síly na kvádr nepůsobily, bylo by její působiště ve středu spodní strany kvádru. Na kvádr působí ale ještě shora tečná síla a na styku s podložkou třecí síla. Kvádr se pohybuje rovnoměrně přímočaře, takže výslednice sil musí být nulová. Tečná síla shora je stejně velká jako třecí síla, ale jsou opačně orientované a mají tendenci deformovat kvádr ve smyku. Působiště tlakové síly od podložky se v okamžiku, kdy začne působit tečná síla shora, bude posouvat doprava k okraji kvádru a ten se bude chtít překlopit přes krajní hranu. V mezním případě působí tlaková síla až na úrovni hrany.
Z rovnosti momentu tíhové a tečné síly ke krajní hraně můžeme vyjádřit tečnou sílu, s její pomocí tečné napětí a s využitím Hookova zákona pak úhel smyku.
Nápověda
Nakreslete si do obrázku všechny síly, které působí na kvádr v hraničním případě, kdy by při zvětšení výšky již nebyla splněna podmínka momentové rovnováhy a došlo by místo deformace jen k otočení kvádru. Napište podmínku rovnováhy pro moment tíhové a tečné síly. Z ní vyjádřete tečnou sílu působící na kvádr a s její pomocí tečné napětí. Dále použijte Hookův zákon pro vztah mezi úhlem smyku a tečným napětím.
Řešení
Protože se kvádr pohybuje rovnoměrně přímočaře, je třeba zde uvažovat třecí sílu T od styku kvádru s vodorovnou podlahou, která působí proti směru tečné síly F a má stejnou velikost. Aby došlo k deformaci, tak kvádr musí být v rovnováze. Následující obrázek ukazuje případ, kdy se kvádr ještě nachází v rovnováze, ale při zvýšení výšky by už došlo k otočení.
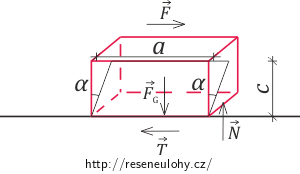
Na obrázku je FG tíhová síla působící v těžišti kvádru a N je reakční síla od podlahy. Kdyby na kvádr působila nulová tečná síla F, síla N by působila v polovině délky a směrem k těžišti. Jakmile se F začne z nuly postupně zvětšovat, síla N se bude postupně posouvat v našem případě směrem doprava. V mezním případě před otočením musíme N uvažovat až na pravém okraji. Z momentové rovnováhy kolem pravého dolního okraje plyne:
\[F_{\mathrm{G}}\frac{a}{2}\,=\,Fc.\tag{1}\]Pak tedy:
\[F\,=\,F_{\mathrm{G}}\frac{a}{2c}.\tag{2}\]Pro tíhovou sílu platí:
\[F_{\mathrm{G}}\,=\,mg\,=\,\rho Vg\,=\,\rho abcg.\tag{3}\]Dosazením (3) do (2) získáme:
\[F\,=\,\frac{\rho a^2 bg}{2}.\tag{4}\]Pro výpočet deformace bude potřeba znát tečné napětí τ. To je ve všech stěnách kromě přední a zadní a je vždy stejně veliké. Protože F působí na stěnu s rozměry a, b, pak tečné napětí je:
\[\tau\,=\,\frac{F}{S}\,=\,\frac{F}{ab}\,=\,\frac{\rho ag}{2}.\tag{5}\]Podle Hookova zákona je úhel smyku:
\[\alpha\,=\,\frac{\tau}{G}.\tag{6}\]Když dosadíme (5) do (6), pak:
\[\alpha\,=\,\frac{\rho ag}{2G}.\tag{7}\]Nyní už stačí jenom číselně dosadit do (7), takže:
\[\alpha\,=\,\frac{8000{\cdot}0{,}6{\cdot}9{,}81}{2{\cdot}80\cdot10^{9}} \mathrm{rad}\,=\,2{,}94{\cdot}10^{-7} \mathrm{rad}.\]Odpověď
Úhel smyku je:
\[\alpha\,=\,2{,}94{\cdot}10^{-7} \mathrm{rad}.\]

