Jeřáb zvedá panel
Úloha číslo: 82
Stavební panel má rozměry 2,4 m, 1,2 m, tloušťku 15 cm. Je vyroben z betonu vyztuženého ocelovými pruty tak, že střední hustota materiálu je 3 000 kg·m−3. Ve směru své tloušťky je odlehčen pěti otvory o průměru 6 cm.
a) Určete objem materiálu v panelu a jeho hmotnost.
b) Jak velkou silou musí jeřáb zvedat panel?
c) Jakou práci vykoná jeřáb, když panel zvedne ze země do výšky 42 m při stavbě posledního podlaží?
d) Jak dlouho trvá zvedání panelu, je-li rychlost zvedání 0,25 m·s−1? Jaký je v tomto případě výkon jeřábu?
e) Použité elektromotory mají účinnost 70 %. Jaký musíme zajistit příkon pro zvedání panelu?
f) Ocelové lano má dovolené namáhání 100 MPa a nosnost u tohoto jeřábu se předpokládá nejvýše 5 tun. Jaký bude nejmenší průměr lana?
Zápis
a = 2,4 m rozměr stavebního panelu b = 1,2 m rozměr stavebního panelu c = 15 cm rozměr stavebního panelu ρ = 3000 kg·m−3 střední hustota betonu vyztuženého ocelovými pruty r0 = 6 cm průměr děr h = 42 m výška zvednutí panelu v = 0,25 m·s−1 rychlost zvedání panelu η = 70 % účinnost elektromotoru σ = 700 MPa dovolené namáhání lana M = 5 t maximální nosnost jeřábu m = ? hmotnost panelu V = ? objem panelu F = ? síla, kterou musí jeřáb zvedat panel W = ? práce vykonaná jeřábem t = ? čas potřebný ke zvednutí panelu P' = ? výkon jeřábu P = ? příkon jeřábu d = ? nejmenší průměr lana Nápověda a1) – objem panelu
Nakreslete si obrázek panelu s otvory.
Jaký vzorec platí pro výpočet objemu kvádru?
Jak se nám promítne v objemu kvádru pět otvorů?
Nápověda a2) – hmotnost panelu
Když už znáte objem a je zadaná hustota panelu, jak spočtete jeho hmotnost?
Nápověda b) – síla
Nakreslete si obrázek dané situace a vyznačte síly působící na panel.
Předpokládejte, že jeřáb zvedá panel rovnoměrným přímočarým pohybem. Jaká je výsledná síla působící na panel? Jakou silou působí jeřáb na panel?
Nápověda c) – práce vykonaná jeřábem
Jeřáb působí na panel konstantní silou po dané dráze a síla má směr posunutí.
Jak v této situaci spočítáte práci vykonanou jeřábem?
Nápověda d1) – doba zvedání
Znáte dráhu a rychlost zvedání, která je konstantní. Čas zvedání tedy snadno vyjádříte.
Nápověda d2) – výkon jeřábu
Znáte práci, kterou vykoná jeřáb a čas, po který ji koná.
Jaký vztah platí pro výpočet výkonu?
Nápověda e) – příkon motoru
Příkon motoru vyjadřuje energii, kterou mu dodáváme za jednotku času. Vzhledem k nevyhnutelným ztrátám způsobeným různými odpory proti pohybu je výkon každého zařízení menší než příkon. Účinností motoru pak rozumíme poměr jeho výkonu a potřebného příkonu. Účinnost je bezrozměrné číslo, které vyjádřuje, jak blízko k ideálnímu procesu probíha proces v hodnoceném stroji nebo zařízení. Pomocí účinnosti a výkonu pak můžete vyjádřit hledaný příkon.
Nápověda f1) – napětí lana
Dovolené namáhání je možno vyjádřit také jako maximální napětí, které lze na lano vyvinout. Jak je definované napětí?
Nápověda f2) – průměr lana
Síla, která působí na lano, se rovná tíze nákladu. Znáte i maximální povolené napětí lana. Snadno vyjádříte plochu průřezu lana a odtud jeho průměr.
Číselný výpočet:
a) Objem a hmotnost panelu
\[a\,=\,2{,}4\, \mathrm{m}\] \[b\,=\,1{,}2\, \mathrm{m}\] \[c\,=\,15\, cm=0{,}15\, \mathrm{m }\] \[r_{0}\,=\,3\, \mathrm{cm}\,=\,0{,}03\, \mathrm{m}\] \[\rho\,=\,3\,000\, \mathrm{kg \cdot m^{-3}}\]
\[V\,=\,abc\,-\,5\pi r_0^2 c\] \[V\,=\,\left(2{,}4{\cdot}1{,}2{\cdot} 0{,}15-5{\cdot}3{,}14{\cdot}0{,}03^{2}\cdot0{,}15\right)\,\mathrm{m^3}\] \[V\,=\,\left(0{,}432-0{,}0021\right)\, \mathrm{m^3}\] \[V\,=\,0{,}4299\, \mathrm{m^3}\,\dot=\,0{,}43\ \mathrm{m^3}\] \[m\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)\] \[m\,=\,3\,000{\cdot} 0{,}15\left(2{,}4{\cdot} 1{,}2\,-\,5{\cdot} 3{,}14{\cdot} 0{,}03^2\right)\,\mathrm{kg}\] \[m\,=\,1\,290\, \mathrm{kg}\]b) Síla, kterou jeřáb zvedá panel
\[m\,=\,1\,290\, \mathrm{kg}\] \[g\,=\,9{,}81\, \mathrm{m \cdot s^{-2}}\]
\[F\,=\,mg\] \[F\,=\,1\,290{\cdot}9{,}81\,\mathrm{N}\] \[F\,=\,12\,655\, \mathrm{N}\,\dot=12{,}7\ \mathrm{kN}\]c) Práce vykonaná jeřábem
\[F\,=\,12\,655\, \mathrm{N}\] \[s\,=\,42\, \mathrm{m}\]
\[W\,=\,Fs\] \[W\,=\,12\,655{\cdot}42\,\mathrm{J}\] \[W\,=\,531\,510\, \mathrm{J}\,\dot=531{,}5\ \mathrm{kJ}\]d1) Doba zvedání panelu
\[s\,=\,42\, \mathrm{m}\] \[v\,=\,0{,}25\, \mathrm{m \cdot s^{-1}}\]
\[t\,=\,\frac{s}{v}\] \[t\,=\,\frac{42}{0{,}25}\,\mathrm{s}\] \[t\,=\,168\, \mathrm{s}\,=\,2\,\mathrm{min}\,48\, \mathrm{s}\]d2) Výkon jeřábu
\[W\,=\,531\,510\, \mathrm{J}\] \[t\,=\,168\, \mathrm{s}\]
\[P^{'}\,=\,\frac{W}{t}\] \[P^{'}\,=\frac{531\,510}{168}\,\mathrm{W}\] \[P^{'}\,=\,3\,164\, \mathrm{W}\,\dot=\,3{,}2\ \mathrm{kW}\]e) Příkon jeřábu
\[P^{'}\,=\,3\,164\, \mathrm{W}\] \[\eta\,=\,0{,}7\]
\[P\,=\,\frac{P^{'}}{\eta}\] \[P\,=\,\frac{3\,164}{0{,}7}\,\mathrm{W}\,=\,4\,520\, \mathrm{W}\,\dot=\,4{,}5\ \mathrm{kW}\]f) Průměr lana
\[M\,=\,5\, \mathrm{t}\,=\,5\,000\, \mathrm{kg}\] \[g\,=\,9{,}81\, \mathrm{m \cdot s^{-2}}\] \[\sigma\,=\,100\, \mathrm{MPa}\,=\,10^{8}\,\mathrm{Pa}\]
\[d\,=\,\sqrt{\frac{4Mg}{\sigma\pi}}\] \[d\,=\,\sqrt{\frac{4{\cdot}5\,000{\cdot}9{,}81}{10^{8}\cdot3{,}14}}\,\mathrm{m}\,=\,0{,}025\,\mathrm{m}\,=\,2{,}5\, \mathrm{cm}\]Odpověď
a) Objem panelu je \[V\,=\,abc\,-\,5{\pi}r_{0}^{2}c\,=\,0{,}4299\,\mathrm{m^3}\,\dot=\,0{,}43\ \mathrm{m^3}.\]
Hmotnost panelu je \[m\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)\,=\,1\,290\,\mathrm{kg}.\]
b) Jeřáb musí zvedat panel sílou rovnou \[F\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)g\,=\,12\,655\,\mathrm{N}\,\dot=\,12{,}7\, \mathrm{kN}.\]
c) Při zvedání panelu do výšky 42 m vykoná jeřáb práci rovnou \[W\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)gs\,=\,531\,510\,\mathrm{J}\,\dot=\,531{,}5\ \mathrm{kJ}.\]
d) Jeřáb zvedá panel rychlostí 0,25 ms-1 po dobu \[t\,=\,\frac{s}{v}\,=\,2\,\mathrm{min}\,48\,\mathrm{s}.\]
V tomto případě je výkon jeřábu roven \[P^{'}\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{t}\,=\,3\,164\, \mathrm{W}\,\dot=\,3{,}2\ \mathrm{kW}.\]
e) Příkon, který musíme zajistit, je roven \[P\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{\eta t}\,=\,4\,520\, \mathrm{W}\,\dot=\,4{,}5\ \mathrm{kW}.\]
f) Nejmenší průměr lana bude \[d\,=\,\sqrt {\frac{4Mg}{\sigma \pi}}\,=\,2{,}5\, \mathrm{cm}.\]
Celkové řešení bodu a) – objem a hmotnost panelu
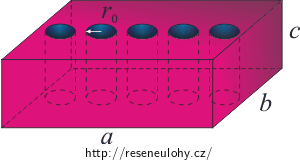
V matematických tabulkách můžeme najít vzorec pro objem kvádru:
\[V\,=\,abc\,.\]V……objem kvádru
a,b,c…rozměry kvádru
Když máme v kvádru (panelu) vyřezanou nějakou část, bude výsledný objem menší o objem této části.
V našem případě máme v panelu pět otvorů ve tvaru válce o daném průměru. Objem každého otvoru je:
\[V\,=\,\pi r_0^2 c\,.\]V…objem vyřezané části
r0…poloměr otvoru
c…výška válce (otvoru)
Pro výšku válce platí, že se rovná tloušťce panelu.
Nyní objemy válců odečteme od celkového objemu panelu. Dostaneme:
\[V\,=\,abc\,-\,5\pi r_0^2 c\,,\tag{1}\] \[V\,=\,\left(2{,}4{\cdot} 1{,}2{\cdot}0{,}15\,-\,5{\cdot} 3{,}14{\cdot} 0{,}03^2{\cdot}0{,}15\right)\,\mathrm{m^3},\] \[V\,=\,0{,}4299\, \mathrm{m^3}\,\dot=\,0{,}43\ \mathrm{m^3}.\]Pro hmotnost při daném objemu a hustotě platí:
\[m\,=\,\rho V\,.\]m… hmotnost panelu
ρ… hustota panelu
V… objem panelu
Za V dosadíme ze vztahu (1):
\[m\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)\,,\tag{2}\] \[m\,=\,3\,000\,\cdot 0{,}15\left(2{,}4{\cdot} 1{,}2\,-\,5{\cdot} 3{,}14{\cdot} 0{,}03^2\right)\,\mathrm{kg},\] \[m\,=\,1\,290\, \mathrm{kg}.\]Odpověď:
Objem panelu je \[V\,=\,0{,}4299\, \mathrm{m^3}\,\dot=\,0{,}43\ \mathrm{m^3}.\]
Hmotnost panelu je \[m\,=\,1\,290\,\mathrm{kg}.\]
Celkové řešení bodu b) – síla, kterou jeřáb zvedá panel
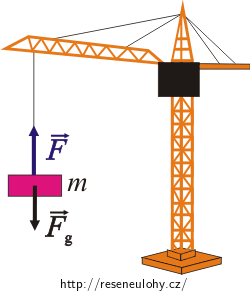
\(\vec{F}\)… síla, kterou působí na panel jeřáb
\(\vec{F}_\mathrm{g}\)… tíhová síla
Výsledná síla působící na panel je při rovnoměrném přímočarém pohybu rovna nule. Síla, kterou působí na panel jeřáb, je rovna tíhové síle působící na panel:
\[F\,=\,F_\mathrm{g}\,=\,mg.\]F… síla, kterou působí na panel jeřáb
Fg… tíhová síla
m… hmotnost panelu
g… tíhové zrychlení
Z předchozího bodu již známe hmotnost panelu m a z fyzikálních tabulek zjistíme hodnotu tíhového zrychlení:
\[g\,=\,9{,}81\,\mathrm{m \cdot s^{-2}}.\]Za m dosadíme ze vztahu (2):
\[F\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)g,\tag{3}\] \[F\,=\,1\,290\,\cdot9{,}81\,\mathrm{N},\] \[F\,=\, 12\,655\, \mathrm{N}\,\dot=\,12{,}7\ \mathrm{kN}.\]Odpověď: Jeřáb musí zvedat panel silou rovnou \[F\,=\,12\,655\,\mathrm{N}\,\dot=\,12{,}7\,\mathrm{kN}.\]
Celkové řešení bodu c) – práce vykonaná jeřábem
V případě, kdy působí konstantní síla ve směru posunutí panelu, můžeme práci spočítat podle vztahu:
\[W\,=\,Fs\,.\]W… vykonaná práce
F… síla, kterou jeřáb působí na panel
s… dráha, na které působí jeřáb sílou F
Za F dosadíme ze vztahu (3):
\[W\,=\,\rho c\left(ab\,-\,5\pi r_0^2\right)gs\,,\tag{4}\] \[W\,=\,12\,655\,\cdot42\,\mathrm{J},\] \[W\,=\,531\,510\,\mathrm{J}\,\dot=\,531{,}5\ \mathrm{kJ}.\]Odpověď: Při zvedání panelu do výšky 42 m vykoná jeřáb práci rovnou \[W\,=\,531\,510\,\mathrm{J}\,\dot=\,531{,}5\ \mathrm{kJ}.\]
Celkové řešení bodu d) – doba zvedání panelu, výkon jeřábu
Pohyb panelu je rovnoměrný přímočarý, takže rychlost vyjádříme pomocí vztahu:
\[v\,=\,\frac{s}{t}\,.\]v… rychlost
s… dráha
t… čas (doba)
Odtud dostáváme pro čas t:
\[t\,=\,\frac{s}{v}\,,\] \[t\,=\,\frac{42}{0{,}25}\,\mathrm{s},\] \[t\,=\,168\, \mathrm{s}\,=\,2\, \mathrm{min}\,48\, \mathrm{s}.\]Výkon je práce vykonaná za jednotku času. Když si to vyjádříme pomocí vztahu, dostaneme:
\[P^{'}\,=\,\frac{W}{t}\,.\]P'… výkon jeřábu
W… vykonaná práce
t… doba, po kterou koná práci
V předchozích úlohách jsme si spočítali vykonanou práci W a také dobu zvedání.
Za práci W dosadíme ze vztahu (4):
\[P^{'}\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{t}\,,\tag{5}\] \[P^{'}\,=\,\frac{531\,510}{168}\,\mathrm{W},\] \[P^{'}\,=\,3\,164\, \mathrm{W}\,\dot=\,3{,}2\ \mathrm{kW}.\]Odpověď:
Jeřáb zvedá panel rychlostí 0,25 ms-1 po dobu \(t\,=\,2\,\mathrm{min}\,48\,\mathrm{s}.\)
V tomto případě je užitečný výkon roven \(P^{'}\,=\,3\,164\, \mathrm{W}\,\dot=\,3{,}2\, \mathrm{kW}.\)
Celkové řešení bodu e) – příkon jeřábu
Matematické vyjádření vztahu pro účinnost:
\[\eta=\frac{P^{'}}{P}.\]η… účinnost
P'… výkon motoru
P… příkon motoru
Hledaný příkon pro zvedaní panelu vyjádříme z tohoto vztahu vynásobením celé rovnice příkonem P a následným vydělěním účinností \(\eta\).
Dostaneme:
\[P\,=\,\frac{P^{'}}{\eta}\,.\]Za P' dosadíme ze vztahu (5):
\[P\,=\,\frac {\rho c\left(ab\,-\,5\pi r_0^2\right)gs}{\eta t}\,,\tag{6}\] \[P\,=\,\frac{3\,115}{0{,}7}\,\mathrm{W},\] \[P\,=\,4\,450\, \mathrm{W}\,\dot=\,4{,}5\ \mathrm{kW}.\]Odpověď: Musíme zajistit příkon \(P\,=\,4\,450\, \mathrm{W}\,\dot=\,4{,}5\ \mathrm{kW}\).
Celkové řešení bodu f) – průměr lana
Dovolené namáhání je možno vyjádřit také jako maximální napětí, které lze na lano vyvinout.
Normálové napětí je podíl síly F a plochy S, na kterou síla F působí:
\[\sigma \,=\,\frac{F}{S}\,.\tag{7}\]σ… napětí
F… síla
S… obsah plochy
Vztah pro tíhu je:
\[F\,=\,Mg\,.\]Dosadíme do vztahu (7):
\[\sigma \,=\, \frac {Mg}{S}\,.\]σ… napětí
M… nosnost lana
g… tíhové zrychlení
S… obsah plochy průřezu
Odtud:
\[S\,=\, \frac {Mg}{\sigma}\,.\tag{8}\]Plocha průřezu lana představuje kruh. Pro obsah kruhu platí:
\[S\,=\,\pi \frac {d^2}{4}\,.\]d… průměr lana
Dosadíme do vztahu (8):
\[\pi \frac {d^2}{4}\,=\,\frac{Mg}{\sigma}\,.\]Odtud úpravami získáme hledaný průměr:
\[d\,=\,\sqrt {\frac{4Mg}{\sigma \pi}}\,,\] \[d\,=\,\sqrt{\frac{4\,\cdot\,5\,000\,\cdot9{,}81}{10^{8}\cdot3{,}14}}\,\mathrm{m},\] \[d\,=\,0{,}025\, \mathrm{m}=2{,}5\, \mathrm{cm}.\]Odpověď: Nejmenší průměr lana bude d = 2,5 cm.





