Přecházení po loďce

Úloha číslo: 1136

O jakou vzdálenost se přemístí loďka stojící na vodě, přejde-li člověk o hmotnosti 70 kg ze zádi na příď lodi? Délka lodi je 2,5 m, její hmotnost 100 kg. Odpor vody a naklonění loďky zanedbejte.

Zápis

m = 70 kg hmotnost člověka

M = 100 kg hmotnost loďky

L = 2,5 m délka loďky

x = ? posun loďky ve vodorovném směru
Nápověda 1
Ještě předtím, než se zamyslíte nad metodou řešení úlohy, určete, jaké vnější síly na nepohybující se soustavu loďka–člověk působí. Která síla způsobí pohyb loďky, když po ní začne člověk přecházet?
Řešení nápovědy 1
Budeme-li uvažovat soustavu loďka–člověk jako jeden celek, působí na ni tyto vnější síly:
- tíhová síla F_G směrem svisle dolů,
- vztlaková síla F_vz směrem svisle vzhůru.
Výslednice těchto sil je nulová.

Příčinou posuvného pohybu loďky ve vodorovném směru je třecí síla mezi botami člověka a dnem loďky; ta ovšem není vnější silou.
Popis metody řešení
Využijeme právě zjištěné skutečnosti, že výslednice vnějších sil působících na soustavu loďka–člověk je v každém okamžiku nulová. Podle 1. Newtonova zákona tedy těžiště soustavy bude setrvávat v klidu nebo rovnoměrném přímočarém pohybu. V našem případě je těžiště soustavy na počátku v klidu, a protože neexistuje vnější síla, která by mu udělila nějaké zrychlení, bude setrvávat v klidu po celou dobu přechodu člověka po loďce. Stručně lze tento poznatek shrnout tak, že v naší soustavě se poloha těžiště zachovává. Z této skutečnosti při řešení úlohy vyjdeme.
Nápověda 2
Nejprve určíme polohu těžiště soustavy předtím, než se člověk začal pohybovat. Do obrázku výše vhodně zaveďte souřadný systém, příď loďky umístěte do jeho počátku. Vyznačte polohu těžiště loďky a těžiště člověka a jejich souřadnice. Kterou souřadnici těžiště budeme výpočtem určovat?
Řešení nápovědy 2
Zavedení souřadnic ukazuje obrázek níže.

Protože nás zajímá pouze posun loďky ve vodorovném směru, budeme určovat pouze x-ovou souřadnici těžiště soustavy x_T1.
Nápověda 3
Vzpomeňte si na vztah pro polohu těžiště soustavy hmotných bodů a dosaďte do něj souřadnice určené v předchozím kroku. (Protože pracujeme s tělesy, budeme k výpočtu přistupovat tak, že celou hmotnost tělesa – loďky a člověka – soustředíme do jeho těžiště.)
Řešení nápovědy 3
Pro x-ovou souřadnici těžiště n hmotných bodů platí (viz například Těžiště různě uspořádaných soustav koulí):
\[x_\mathrm{T1}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}}.\tag{1}\]
V případě naší soustavy dosadíme do vztahu (1) hmotnosti a souřadnice těžiště člověka a loďky:
\[x_\mathrm{T1}\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^2{m_\mathrm{i}}}\,=\,\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}.\tag{2}\]
Nápověda 4
Nyní uvažujme, že po přejití člověka ze zádi na příď se loďka posunula o vzdálenost x. Na jakou stranu? Nakreslete obrázek popisující novou situaci a opět do něj vyznačte polohu těžiště loďky a člověka.
Řešení nápovědy 4
Z pohledu naší souřadné soustavy se po přechodu člověka ze zádi na příď loďka posunula o vzdálenost x doprava – novou situaci ukazuje obrázek níže:
Nápověda 5
Podobně jako pro první situaci obecně vyjádřete x-ovou souřadnici těžiště soustavy, kterou budeme dále označovat jako x_T2. Z úvodu naší úlohy víme, že poloha těžiště soustavy se nemění, jeho souřadnice se tedy také zachovává. Z této rovnosti vyjádřete hledanou vzdálenost x.
Řešení nápovědy 5
Souřadnici těžiště soustavy určíme opět podle vztahu (1) – nyní bude mít výpočet tuto podobu:
\[x_\mathrm{T2}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}x_\mathrm{i}'}}{\sum_{i=1}^n{m_\mathrm{i}}} \,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}.\tag{3}\]
Protože poloha těžiště naší soustavy se během celého pohybu zachovávala, platí:
\[x_\mathrm{T1}\,=\,x_\mathrm{T2}.\]
Srovnáním vztahů (2) a (3) dostaneme:
\[\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}\,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}.\]
Úpravami dostaneme:
\[M\frac{L}{2}\,+\,mL\,=\,mx\,+\,M(x\,+\,\frac{L}{2}),\] \[mL\,=\,mx\,+\,Mx,\] \[x\,=\,\frac{mL}{M\,+\,m}.\]
Číselně:
\[x\,=\,\frac{70{\cdot}2{,}5}{100\,+\,70}\,\mathrm{m}\,\dot=\,1{,}03\,\mathrm{m}.\]
Loďka se ve vodorovném směru posune přibližně o 1,03 m.
Celkové řešení
Budeme-li uvažovat soustavu loďka–člověk jako jeden celek, působí na ni tyto vnější síly:
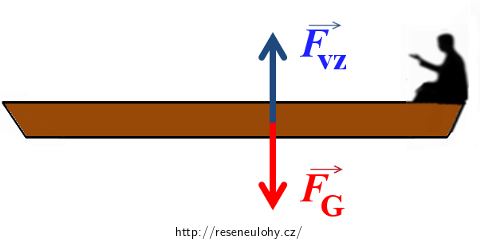
- tíhová síla F_G směrem svisle dolů,
- vztlaková síla F_vz směrem svisle vzhůru.
Výslednice těchto sil je nulová.

Příčinou posuvného pohybu loďky ve vodorovném směru je třecí síla mezi botami člověka a dnem loďky; ta ovšem není vnější silou.

Využijeme právě zjištěné skutečnosti, že výslednice vnějších sil působících na soustavu loďka–člověk je v každém okamžiku nulová. Podle 1. Newtonova zákona tedy těžiště soustavy bude setrvávat v klidu nebo rovnoměrném přímočarém pohybu. V našem případě je těžiště soustavy na počátku v klidu, a protože neexistuje vnější síla, která by mu udělila nějaké zrychlení, bude setrvávat v klidu po celou dobu přechodu člověka po loďce. Stručně lze tento poznatek shrnout tak, že v naší soustavě se poloha těžiště zachovává. Z této skutečnosti při řešení úlohy vyjdeme.

Do nákresu situace vhodně zavedeme souřadný systém a zakreslíme známé i hledané veličiny:

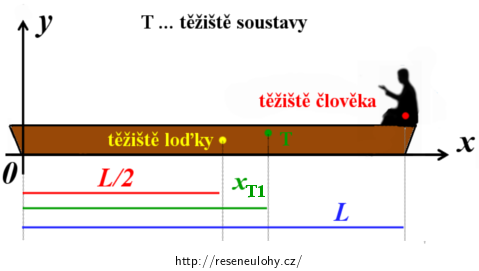
Protože nás zajímá pouze posun loďky ve vodorovném směru, budeme určovat pouze x-ovou souřadnici těžiště soustavy x_T1.

Pro x-ovou souřadnici těžiště n hmotných bodů platí (viz například Těžiště různě uspořádaných soustav koulí):
\[x_\mathrm{T1}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}}.\tag{1}\]
V případě naší soustavy dosadíme do vztahu (1) hmotnosti a souřadnice těžiště člověka a loďky:
\[x_\mathrm{T1}\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^2{m_\mathrm{i}}}\,=\,\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}.\tag{2}\]
Z pohledu naší souřadné soustavy se po přechodu člověka ze zádi na příď loďka posunula o vzdálenost x doprava – novou situaci ukazuje obrázek níže:

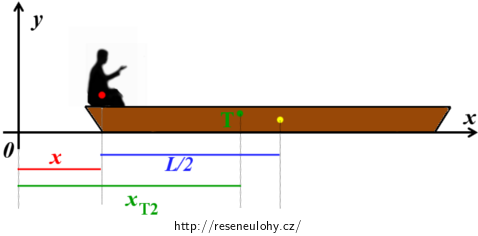
Souřadnici těžiště soustavy určíme opět podle vztahu (1) – nyní bude mít výpočet tuto podobu:
\[x_\mathrm{T2}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}x_\mathrm{i}'}}{\sum_{i=1}^n{m_\mathrm{i}}} \,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}.\tag{3}\]
Protože poloha těžiště naší soustavy se během celého pohybu zachovávala, platí:
\[x_\mathrm{T1}\,=\,x_\mathrm{T2}.\]
Srovnáním vztahů (2) a (3) dostáváme:
\[\frac{M\frac{L}{2}\,+\,mL}{M\,+\,m}\,=\,\frac{mx\,+\,M(x\,+\,\frac{L}{2})}{M\,+\,m}.\]
Úpravami:
\[M\frac{L}{2}\,+\,mL\,=\,mx\,+\,M(x\,+\,\frac{L}{2}),\] \[mL\,=\,mx\,+\,Mx,\] \[x\,=\,\frac{mL}{M\,+\,m}.\]
Číselně:
\[x\,=\,\frac{70{\cdot}2{,}5}{100\,+\,70}\,\mathrm{m}\,\dot=\,1{,}03\,\mathrm{m}.\]
Loďka se ve vodorovném směru posune přibližně o 1,03 m.
Odpověď
Loďka se ve vodorovném směru posune přibližně o 1,03 m.