Vozík na vzduchové dráze
Úloha číslo: 143
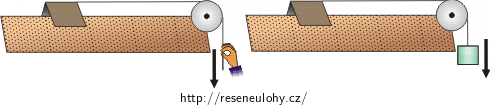
Vozík na vzduchové dráze má hmotnost 250 g a je uváděn do zrychleného pohybu tahem za vlákno přes pevnou kladku. Porovnejte velikost zrychlení vozíku, jestliže
a) táhneme za vlákno rukou silou 0,1 N,
b) zavěsíme na vlákno závaží o tíze 0,1 N.
Odpor vzduchu a hmotnost vlákna a kladky neuvažujte.
Poznámka: Vzduchová dráha je zařízení, na kterém je možný pohyb vozíku (stříšky) bez tření podložky. Proud vzduchu zespoda nadnáší vozík.
Zápis
mv = 250 g hmotnost vozíku F = 0,1 N velikost síly, kterou působí ruka prostřednictvím vlákna na vozík FGz = 0,1 N velikost tíhové síly působící na závaží a1 = ? velikost zrychlení vozíku, jestliže táhneme za vlákno rukou silou 0,1 N a2 = ? velikost zrychlení vozíku, jestliže zavěsíme na vlákno závaží o tíze 0,1 N Nápověda 1a – síly působící na vozík, pohybová rovnice
Nakreslete si obrázek a vyznačte do něj síly působící na vozík v případě, že za vlákno táhneme silou o velikosti 0,1 N. Napište pohybovou rovnici pro vozík.
Nápověda 2a – pohybová rovnice skalárně
Pohybovou rovnici ze vztahu (1) přepište skalárně a vyjádřete velikost zrychlení a1.
Nápověda 1b – síly působící na vozík a na závaží, pohybové rovnice
Nakreslete si obrázek a vyznačte do něj síly působící na vozík a na závaží. Napište pohybovou rovnici pro vozík a pro závaží.
Nápověda 2b – pohybové rovnice skalárně, tah vlákna
Pohybové rovnice ze vztahu (7) a (8) přepište skalárně. Uvědomte si, jaký je vztah mezi tahy vlákna T a T'.
Nápověda 3b – výpočet zrychlení
Pomocí rovnic (10) a (11) vypočtěte velikost zrychlení a2.
Poznámka
Zrychlení a1 je větší než zrychlení a2. Je to proto, že v prvním případě síla o velikosti 0,1 N působí přímo na vozík a uděluje zrychlení jen jemu. Ve druhém případě síla 0,1 N, která je rovna tíze závaží, uděluje zrychlení nejen vozíku, ale i samotnému závaží.
CELKOVÉ ŘEŠENÍ
Síly působící na vozík v případě a):
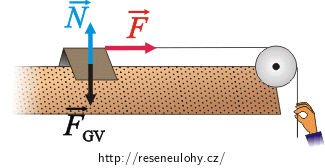
\(\vec{F}\)…síla, kterou působí ruka prostřednictvím vlákna na vozík,
\(\vec{N}\)…síla, kterou tlačí vzduch zespoda na vozík,
\(\vec{F}_\mathrm{G_v}\)…tíhová síla působící na vozík.
Pohybová rovnice:
\[\vec{F}_\mathrm{G_v}+\vec{N}+\vec{F}\,=\, m_\mathrm{v}\vec{a_1},\tag{1}\]\(m_\mathrm{v}\)…hmotnost vozíku,
\(\vec{a}_1\)…zrychlení vozíku.
Abychom pohybovou rovnici mohli přepsat skalárně, zvolíme vhodně souřadný systém. Osu x volíme ve směru pohybu vozíku. Osa y je kolmá na osu x.
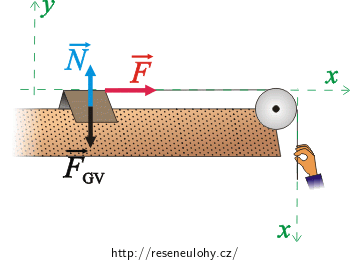
Pohybová rovnice skalárně:
\[x:\qquad F\,=\,m_\mathrm{v} a_1,\tag{2}\] \[y:\qquad N - F_\mathrm{G_v} \,=\,0.\tag{3}\]Ve směru osy y se vozík nepohybuje, proto je zrychlení rovno nule.
Ze vztahu (2) vyjádříme velikost zrychlení a1:
\[ a_1\,=\,\frac{F}{m_\mathrm{v}}.\tag{4}\]Dosadíme číselně:
\[ a_1\,=\,\frac{0{,}1}{0{,}25}\,\mathrm{m \cdot s^{-2}}\,=\, 0{,}4\,\mathrm{m \cdot s^{-2}}.\tag{5}\]Síly působící na vozík a na závaží v případě b):
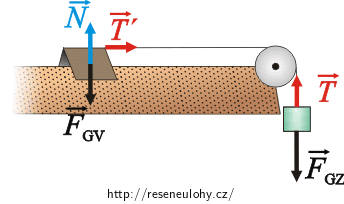
Vozík:
\(\vec{N}\)…síla, kterou tlačí vzduch zespoda na vozík,
\(\vec{F}_\mathrm{G_v}\)…tíhová síla působící na vozík,
\(\vec{T}\prime\)…síla, kterou působí závaží prostřednictvím vlákna na vozík.
Závaží:
\(\vec{F}_\mathrm{G_z}\)…tíhová síla působící na závaží,
\(\vec{T}\)… síla, kterou působí vozík prostřednictvím vlákna na závaží.
Pohybové rovnice:
Pohybová rovnice pro vozík:
\[\vec{F}_\mathrm{G_v}+\vec{N}+\vec{T}\prime\,=\, m_\mathrm{v}\vec{a}_2.\tag{6}\]Pohybová rovnice pro závaží:
\[\vec{F}_\mathrm{G_z}+\vec{T}\,=\,m_\mathrm{z}\vec{a}_2,\tag{7}\]\(m_\mathrm{v}\)…hmotnost vozíku,
\(m_\mathrm{z}\)…hmotnost závaží,
\(\vec{a}_2\)…zrychlení vozíku a závaží.
Abychom pohybové rovnice mohli přepsat skalárně, zvolíme vhodně souřadný systém. Osu x volíme ve směru pohybu vozíku (závaží). Osa y je kolmá na osu x.
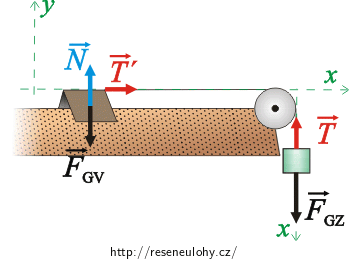
Pohybové rovnice skalárně:
Pohybová rovnice pro vozík:
\[x:\qquad T\prime\,=\,m_\mathrm{v}a_2,\tag{8}\] \[y:\qquad N - F_\mathrm{G_v}\,=\,0.\tag{9}\]Ve směru osy y se vozík nepohybuje, proto je zrychlení rovno nule.
Pohybová rovnice pro závaží:
\[x:\qquad F_\mathrm{G_z}-T\,=\,m_\mathrm{z}a_2.\tag{10}\]Jelikož hmotnost kladky zanedbáváme, nemá žádný moment setrvačnosti a neovlivňuje tah vlákna. Vozík působí prostřednictvím vlákna na závaží a závaží zase naopak na vozík. Podle 3. Newtonova zákona platí pro velikosti sil:
\[|\vec{T}| \,=\, |\vec{T}\prime|.\]Přepíšeme rovnici (10):
\[T\,=\,m_\mathrm{v}a_2.\tag{11}\]Sečteme rovnice (10) a (11):
\[F_\mathrm{G_z}\,=\,m_\mathrm{z}a_2+m_\mathrm{v}a_2,\] \[F_\mathrm{G_z}\,=\,(m_\mathrm{z}+m_\mathrm{v})a_2,\] \[a_2\,=\,\frac{F_\mathrm{G_z}}{m_\mathrm{z}+m_\mathrm{v}}.\]Hmotnost závaží je \(m_\mathrm{z}\,=\,\frac{F_\mathrm{G_z}}{g}\), platí:
\[a_2\,=\,\frac{F_\mathrm{G_z}}{\frac{F_\mathrm{G_z}}{g}+m_\mathrm{v}}.\tag{12}\]Do vztahu (12) dosadíme číselně:
\[a_2\,=\,\frac{0{,}1}{\frac{0{,}1}{10}\,+\,0{,}25}\,\mathrm{m\cdot s^{-2}}\,=\, \frac{0{,}1}{0{,}26}\,\mathrm{m\cdot s^{-2}}\,=\,0{,}38\,\mathrm{m\cdot s^{-2}}.\tag{13}\]CELKOVÁ ODPOVĚĎ
Velikost zrychlení vozíku, jestliže táhneme za vlákno rukou silou 0,1 N, je
\[a_1\,=\,\frac{F}{m_\mathrm{v}}\,=\,0{,}4\,\mathrm{m\cdot s^{-2}}\,.\]Velikost zrychlení vozíku, jestliže zavěsíme na vlákno závaží o tíze 0,1 N, je
\[ a_2\,=\,\frac{F_\mathrm{G_z}}{\frac{F_\mathrm{G_z}}{g}+m_\mathrm{v}}\,=\,0{,}38\,\mathrm{m\cdot s^{-2}}\,.\]Poznámka: Zrychlení a1 je větší než zrychlení a2. Je to proto, že v prvním případě síla o velikosti 0,1 N působí přímo na vozík a uděluje zrychlení jen jemu. Ve druhém případě síla 0,1 N, která je rovna tíze závaží, uděluje zrychlení nejen vozíku, ale i samotnému závaží.





