Sbírka řešených úloh

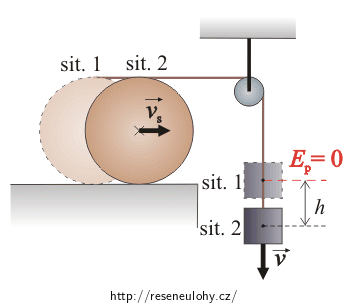
Válec a vlákno

Úloha číslo: 536

Homogenní plný válec o hmotnosti M a poloměru R leží na vodorovné podložce. Na válci je navinuto vlákno, které je ve vodorovném směru vedeno přes pevnou kladku. Na volném konci vlákna je zavěšeno závaží o hmotnosti m.

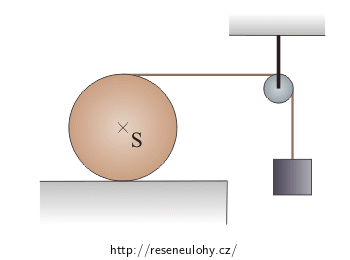
Klesající závaží uvede prostřednictvím vlákna válec do valivého pohybu na vodorovné rovině bez smyku.

a) Určete zrychlení a_S hmotného středu válce.

b) Určete velikost síly klidového tření mezi válcem a vodorovnou rovinou.

(Hmotnost vlákna a kladky neuvažujte, tření kladky zanedbejte.)

• Zápis

  M	hmotnost válce
  R	poloměr válce
  m	hmotnost závaží
  aS = ?	zrychlení hmotného středu válce
  Ft = ?	velikost síly klidového tření mezi válcem a vodorovnou rovinou

• Rozbor

  Zrychlení hmotného středu je možné určit dvěma způsoby. Buď pomocí zákona zachování mechanické energie (A), nebo přes impulsové věty (B).

  V prvním případě je třeba zvolit dvě vhodné situace, ve kterých budete mechanickou energii soustavy srovnávat. Uvědomte si, že válec se jednak otáčí, jednak koná posuvný pohyb.

  Při řešení přes impulsové věty je třeba uvážit, které všechny síly na válec a závaží působí a co platí pro jejich výslednice. Zvažte, jaký bude směr třecí síly působící na válec. Pro válec je třeba napsat i druhou větu impulsovou. Rozhodněte, vzhledem ke kterému bodu budete momenty sil psát, a s ohledem na to napište správný vztah pro moment setrvačnosti válce vzhledem k ose procházející tímto bodem.

• Moment setrvačnosti

  Moment setrvačnosti válce o hmotnosti M a poloměru R při otáčení podle osy symetrie je podle tabulek \(J=\frac{1}{2}MR^2\).

• Nápověda 1A – zákon zachování mechanické energie

  Porovnejte energie soustavy válec–závaží v situaci v klidu a po chvíli pohybu. Nezapomeňte zvolit nulovou hladinu potenciální energie.

• Řešení nápovědy 1A

  

  Situace 1 popisuje soustavu v klidu, proto je kinetická energie soustavy nulová. Zvolme nulovou hladinu potenciální energie, aby závaží mělo v této situaci nulovou i potenciální energii. Potenciální energie válce se během valení nemění: označme ji \(E_\mathrm{pv}\):

  \[E_1=E_\mathrm{k1}+E_\mathrm{p1}=0+E_\mathrm{pv}=E_\mathrm{pv}.\]

  V situaci 2 závaží kleslo o výšku h. Střed válce získal rychlost v_S a válec se otáčí úhlovou rychlostí ω_S.

  Kinetická energie válce je tedy \(\frac{1}{2}J\omega_\mathrm{S}^2+\frac{1}{2}Mv_\mathrm{S}^2\).

  Závaží se pohybuje rychlostí v, jeho kinetická energie je \(\frac{1}{2}mv^2\).

  Přitom potenciální energie závaží klesla a je rovna \(-mgh\), zatímco potenciální energie válce se nezměnila, je rovna \(E_\mathrm{pv}\):

  \[E_2=E_\mathrm{k2}+E_\mathrm{p2}=\frac{1}{2}mv^2+\frac{1}{2}J\omega_S^2+\frac{1}{2}Mv_\mathrm{S}^2-mhg+E_\mathrm{pv}.\]

  Protože ztráty energie třením na kladce i valivý odpor zanedbáváme a válec neztrácí energii prokluzováním, musí platit zákon zachování mechanické energie:

  \[E_1=E_2.\]

  Proto:

  \[E_\mathrm{pv}=E_\mathrm{k2}+E_\mathrm{p2}=\frac{1}{2}mv^2+\frac{1}{2}J\omega_\mathrm{S}^2+\frac{1}{2}Mv_\mathrm{S}^2-mhg+E_\mathrm{pv}\,.\]

  Upravíme:

  \[mgh=\frac{1}{2}mv^2+\frac{1}{2}J\omega_\mathrm{S}^2+\frac{1}{2}Mv_\mathrm{S}^2\,.\tag{1}\]

• Nápověda 2 A – zákon zachování mechanické energie

  Vyjádřete vzdálenost, o kterou sjelo závaží, pomocí jeho zrychlení. Jaký vztah platí mezi velikostí rychlosti závaží a velikostí rychlosti hmotného středu válce a podobně mezi velikostmi jejich zrychlení?

• Řešení nápovědy 2A

  Závaží sjíždí se stálým zrychlením a, neboť na něj působí stálá síla. Uraženou vzdálenost h můžeme vyjádřit jako:

  \[h=\frac{1}{2}at^2\,.\]

  A protože \(v=at\), potažmo \(t=\frac{v}{a},\)

  pak \(h=\frac{v^2}{2a}.\)

  Velikost rychlosti hmotného středu válce \(v_\mathrm{S}\) je poloviční než rychlost závaží, neboť je v poloviční vzdálenosti od bodu B (bodu kontaktu s podložkou, kolem kterého probíhá otáčení):

  \[v_\mathrm{S}=\frac{v}{2}\,.\]

  A podobně je velikost zrychlení hmotného středu válce \(a_\mathrm{S}\) polovinou zrychlení závaží \(a\):

  \[a_\mathrm{S}=\frac{a}{2}.\]

  Dosadíme do vztahu (1) za \(h\) a za \(\omega_\mathrm{S} = \frac{v_\mathrm{S}}{R}\):

  \[\frac{1}{2}mg\frac{v^2}{a}=\frac{1}{2}mv^2+\frac{1}{2}(\frac{1}{2}MR^2)\frac{v_\mathrm{S}^2}{R^2}+\frac{1}{2}Mv_\mathrm{S}^2\,.\]

  Upravíme:

  \[mg\frac{v^2}{a}=mv^2+\frac{3}{2}Mv_\mathrm{S}^2\,.\]

  Dosadíme za \(v_\mathrm{S}\):

  \[mg\frac{v^2}{a}=mv^2+\frac{3}{8}Mv^2\,,\] \[\frac{mg}{a}=m+\frac{3}{8}M\,,\] \[a=\frac{8mg}{3M+8m}\,,\] \[a_\mathrm{S}=\frac{a}{2}=\frac{4mg}{3M+8m}\,.\]

• Nápověda 1B – impulsové věty

  Jaké síly na válec a závaží působí? Zakreslete je do obrázku.

• Řešení nápovědy 1B

  

  Na válec působí síla tíhová \(\vec{F}_\mathrm{G}=M\vec{g}\), proti ní reakce podložky \(\vec{F}_\mathrm{r}\), dále síla působená vláknem \(\vec{F}_1\) a také síla třecí \(\vec{F}_\mathrm{t}\). Na závaží působí síla tíhová \(\vec{F}\) a síla působená vláknem \(\vec{F_1^,}\).

  Třecí síla směřuje na první pohled nečekaným směrem – ve směru pohybu válce. Můžeme ji nakreslit na druhou stranu a tak s ní počítat. Její velikost nám pak vyjde záporná a usvědčí nás tak z omylu.

• Nápověda 2B – impulsové věty

  Napište, co platí pro výslednici sil působících na závaží a na válec. Rovnice přepište skalárně.

• Řešení nápovědy 2B

  Pro působící síly platí:

  Závaží:

  \[\vec{F} + \vec{F}_1^, = m\vec{a}\,.\]

  Skalárně:

  \[F-F_1^, = ma\,,\] \[mg-F_1^, = ma\,.\tag{2}\]

  Válec:

  \[\vec{F}_\mathrm{G} + \vec{F}_1 +\vec{F}_\mathrm{r} + \vec{F}_\mathrm{t}= M\vec{a}_\mathrm{S}\,.\]

  Skalárně:

  \[F_1+F_\mathrm{t}=M a_\mathrm{S}\,,\tag{3}\]

  \[Mg-F_r=0.\]

  Zrychlení středu válce a_S je proti zrychlení závaží a poloviční: \(a_\mathrm{S}=\frac{a}{2}\) , neboť zrychlení závaží je doslova spojeno se zrychlením bodu A. Bod A zrychluje dvojnásobně proti středu válce, protože je v dvojnásobné vzdálenosti od středu otáčení, kterým je (stále se měnící) bod kontaktu s podložkou.

  Kladka je nehmotná, pro tah vlákna podle 3. Newtonova zákona platí: \(F_1=F_1^,\,.\)

• Nápověda 3B – impulsové věty

  Pro válec napište ještě 2. impulsovou větu. Zvažte, vzhledem ke kterému bodu budete momenty sil vztahovat.

• Řešení nápovědy 3B

  Druhá impulsová věta říká, že časová změna momentu hybnosti soustavy se rovná celkovému momentu vnějších sil:

  \[\vec{M}=\frac{d\vec{L}}{dt}\,.\]

  (\(\vec{M}\) a \(\vec{L}\) jsou vztahovány k témuž bodu.)

  V případě rotace tuhého tělesa kolem pevné osy platí:

  \[L = J \omega\,,\] \[\vec{M}=\frac{d\vec{L}}{dt} = J\vec{\epsilon}\,.\]

  J je moment setrvačnosti tělesa vzhledem k pevné ose procházející bodem, ke kterému vztahujeme momenty sil, a ε je úhlové zrychlení.

  Pro výsledný moment sil působících na válec vzhledem k bodu S platí:

  \[\vec{R} \times \vec{F_1} + \vec{R} \times \vec{F_\mathrm{t}} = J\vec{\epsilon}\,.\]

  Přepíšeme skalárně:

  \[F_1R-F_\mathrm{t}R=J\epsilon\,.\] Pro úhlové zrychlení platí:

  \[\epsilon=\frac{a_\mathrm{S}}{R}\,.\]

  Dosadíme za ε a J:

  \[F_1R-F_\mathrm{t}R=\frac{1}{2}MR^2\frac{a_\mathrm{S}}{R}=\frac{1}{2}MRa_\mathrm{S}\,.\]

  Vydělíme R:

  \[F_1-F_t=\frac{1}{2}Ma_\mathrm{S}\,.\tag{4}\]

• Nápověda 4B – impulsové věty

  Pomocí rovnic (2), (3), (4) vyjádřete hledané zrychlení.

• Řešení nápovědy 4B – impulsové věty

  Sečtením rovnic (3) a (4) dostaneme:

  \[2F_1=\frac{3}{2}Ma_\mathrm{S}\,,\] \[F_1=\frac{3}{4}Ma_\mathrm{S}\,.\]

  Upravme rovnici (2):

  \[a=g-\frac{F_1}{m}=g-\frac{3Ma_\mathrm{S}}{4m}\,.\]

  A protože \(2a_\mathrm{S}=a\):

  \[8ma_\mathrm{S}=4mg-3Ma_\mathrm{S}\,,\] \[a_\mathrm{S}(8m+3M)=4mg\,,\] \[a_\mathrm{S}=\frac{4mg}{8m+3M}\,.\]

• Alternativní řešení B

  Momenty sil působících na válec můžeme vztahovat vůči bodu B, čímž bude nulový moment tíhové síly, třecí síly i reakce podložky.

  Pro výsledný moment sil působících na válec vzhledem k bodu B:

  \[2\vec{R} \times \vec{F_1} = J_\mathrm{B}\vec{\epsilon}\,.\]

  Přepíšeme skalárně:

  \[2RF_1 = J_\mathrm{B}\epsilon\,.\tag{5}\]

  Pro moment setrvačnosti válce vzhledem k ose procházející bodem B platí podle Steinerovy věty:

  \[J_\mathrm{B}=J_\mathrm{S}+MR^2=\frac{1}{2}MR^2+MR^2=\frac{3}{2}MR^2\,.\]

  Za sílu F₁ dosadíme z rovnice (2):

  \[F_1=m(g-a)\,.\]

  Dosadíme do rovnice (5):

  \[2R m(g-a) = \frac{3}{2}MR^2\epsilon\,.\]

  Pro úhlové zrychlení platí:

  \[\epsilon=\frac{a_\mathrm{S}}{R}\,.\]

  Také platí:

  \[a = 2 a_\mathrm{S}\,.\]

  Pak dostáváme:

  \[2R m(g-2a_\mathrm{S}) = \frac{3}{2}MR^2\frac{a_\mathrm{S}}{R}\,.\]

  Vyjádříme zrychlení:

  \[a_\mathrm{S}(3M+8m)=4gm\,,\] \[a_\mathrm{S}=\frac{4gm}{3M+8m}\,.\]

• Nápověda 5B – velikost třecí síly

  Hledanou třecí sílu vyjádřete z rovnice (3).

• Řešení b)

  Z rovnice (4) dosazením za F₁:

  \[F_\mathrm{t}=F_1-\frac{1}{2}Ma_\mathrm{S}=\frac{3}{4}Ma_\mathrm{S}-\frac{1}{2}Ma_\mathrm{S}=\frac{Ma_\mathrm{S}}{4}\,.\] a_S známe: \[F_\mathrm{t}=\frac{Mmg}{8m+3M}\,.\]

• Celkové řešení – pomocí impulsových vět

  a) Zrychlení hmotného středu válce

  Do obrázku nakreslíme síly, které na válec a závaží působí.

  

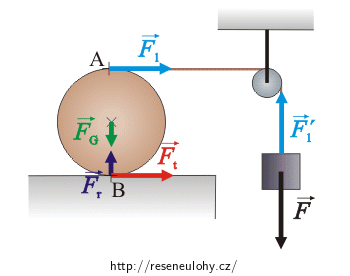
  Na válec působí síla tíhová \(\vec{F}_\mathrm{G}=M\vec{g}\), proti ní reakce podložky \(\vec{F}_\mathrm{r}\), dále síla působená vláknem \(\vec{F}_1\) a také síla třecí \(\vec{F}_\mathrm{t}\). Na závaží působí síla tíhová \(\vec{F}\) a síla působená vláknem \(\vec{F_1^,}\).

  Pro působící síly platí:

  Závaží:

  \[\vec{F} + \vec{F}_1^, = m\vec{a}\,.\]

  Skalárně:

  \[F-F_1^, = ma\,,\] \[mg-F_1^, = ma\,.\tag{1}\]

  Válec:

  \[\vec{F}_\mathrm{G} + \vec{F}_1 +\vec{F}_\mathrm{r} + \vec{F}_\mathrm{t}= M\vec{a}_\mathrm{S}\,.\]

  Skalárně:

  \[F_1+F_\mathrm{t}=M a_\mathrm{S}\,,\tag{2}\]

  \[Mg-F_\mathrm{r}=0\,.\]

  Zrychlení středu válce a_S je proti zrychlení závaží a poloviční: \(a_\mathrm{S}=\frac{a}{2}\,.\)

  Kladka je nehmotná, pro tah vlákna podle 3. Newtonova zákona platí: \(F_1=F_1^,\,.\)

  Pro válec napíšeme ještě 2. impulsovou větu.

  Druhá impulsová věta říká, že časová změna momentu hybnosti soustavy se rovná celkovému momentu vnějších sil:

  \[\vec{M}=\frac{d\vec{L}}{dt}\,.\]

  (\(\vec{M}\) a \(\vec{L}\) jsou vztahovány k témuž bodu.)

  V případě rotace tuhého tělesa kolem pevné osy platí:

  \[L = J \omega\,,\] \[\vec{M}=\frac{d\vec{L}}{dt} = J\vec{\epsilon}\,.\]

  J je moment setrvačnosti tělesa vzhledem k pevné ose procházející bodem, ke kterému vztahujeme momenty sil, a ε je úhlové zrychlení.

  Pro výsledný moment sil působících na válec vzhledem k bodu S platí:

  \[\vec{R} \times \vec{F_1} + \vec{R} \times \vec{F_t} = J\vec{\epsilon}\,.\]

  Přepíšeme skalárně:

  \[F_1R-F_\mathrm{t}R=J\epsilon\,.\] Pro úhlové zrychlení platí:

  \[\epsilon=\frac{a_\mathrm{S}}{R}\,.\]

  Dosadíme za ε a J:

  \[F_1R-F_\mathrm{t}R=\frac{1}{2}MR^2\frac{a_\mathrm{S}}{R}=\frac{1}{2}MRa_\mathrm{S}\,.\]

  Vydělíme R:

  \[F_1-F_\mathrm{t}=\frac{1}{2}Ma_\mathrm{S}\,.\tag{3}\]

  Pomocí rovnic (1), (2), (3) vyjádříme hledané zrychlení.

  Sečtením rovnic (2) a (3) dostaneme:

  \[2F_1=\frac{3}{2}Ma_\mathrm{S}\,,\] \[F_1=\frac{3}{4}Ma_\mathrm{S}\,.\]

  Upravme rovnici (1):

  \[a=g-\frac{F_1}{m}=g-\frac{3Ma_\mathrm{S}}{4m}\,.\]

  A protože \(2a_\mathrm{S}=a\):

  \[8ma_\mathrm{S}=4mg-3Ma_\mathrm{S}\,,\] \[a_\mathrm{S}(8m+3M)=4mg\,,\] \[a_\mathrm{S}=\frac{4mg}{8m+3M}\,.\]  

  Poznámka:

  Momenty sil působících na válec můžeme vztahovat i vůči jinému bodu, např. bodu B, čímž bude nulový moment třecí síly a reakce podložky i moment síly tíhové.

  Zrychlení hmotného středu válce můžeme spočítat také pomocí zákona zachování mechanické energie.

   

  b) Velikost třecí síly

  Hledanou třecí sílu vyjádříme z rovnice (3).

  Z rovnice (3) dosazením za F₁:

  \[F_\mathrm{t}=F_1-\frac{1}{2}Ma_\mathrm{S}=\frac{3}{4}Ma_\mathrm{S}-\frac{1}{2}Ma_\mathrm{S}=\frac{Ma_\mathrm{S}}{4}\,.\] a_S známe: \[F_\mathrm{t}=\frac{Mmg}{8m+3M}\,.\]

• Odpověď

  Zrychlení středu válce je vyjádřeno vztahem \(a_\mathrm{S}=\frac{4mg}{3M+8m}\,.\)

  Síla klidového tření \(F_\mathrm{t}=\frac{Mmg}{8m+3M}.\)