Soustava Země–Měsíc
Úloha číslo: 1133
Určete polohu hmotného středu soustavy Země–Měsíc, jestliže víte, že hmotnost Země je 81x větší než hmotnost Měsíce a vzdálenost středů je 384 000 km. Porovnejte vzdálenost hmotného středu této soustavy od středu Země s jejím poloměrem.
Zápis
m hmotnost Měsíce M = 81m hmotnost Země a = 384 000 km vzdálenost středů Měsíce a Země xT = ? vzdálenost hmotného středu soustavy od středu Země Nápověda 1
Výše uvedenou situaci zakreslete do obrázku a vhodně do ní zaveďte souřadný systém. Které souřadnice hmotného středu soustavy musíte vypočítat a které se dají určit pouze z obrázku, bez výpočtu?
Nápověda 2
V dané situaci můžeme Zemi a Měsíc považovat za hmotné body, neboť jejich vzdálenost (384 000 km) je mnohonásobně větší než jejich rozměry (poloměr Země je 6 378 km). Pro výpočet neznámé xT proto použijte vztah pro polohu hmotného středu soustavy hmotných bodů – jak tento vztah vypadá?
Nápověda 3
Do vztahu (1) dosaďte konkrétní hodnoty a číselně dopočítejte. Vyjádřete vzdálenost hmotného středu soustavy od středu Země jako procentuální část zemského poloměru.
Celkové řešení
Na úvod nakreslíme obrázek situace (viz níže). Zemi a Měsíc můžeme považovat za hmotné body, neboť jejich vzdálenost (384 000 km) je mnohonásobně větší než jejich rozměry (poloměr Země je 6 378 km). Zvolený souřadný systém má počátek ve středu Země a je zvolen tak, že osa x prochází středem Měsíce:
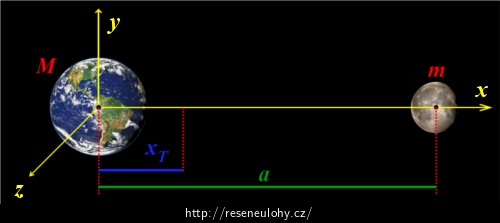
Protože v takto zvoleném souřadném systému leží hmotné středy obou uvažovaných těles na ose x, bude také hmotný střed jejich soustavy ležet na ose x. Všechny body na ose x mají ale y-ovou a z-ovou souřadnici nulovou, tedy také pro souřadnice yT, zT hmotného středu platí:
\[y_\mathrm{T}\,=\,z_\mathrm{T}\,=\,0.\]Pro výpočet zbývající neznámé xT použijeme obecný vztah pro polohu hmotného středu soustavy n hmotných bodů:
\[\vec{r}_\mathrm{T}\,=\,\frac{\sum_{i=1}^n{m_\mathrm{i}\vec{r}_\mathrm{i}}}{\sum_{i=1}^n{m_\mathrm{i}}},\]kde mi jsou hmotnosti jednotlivých hmotných bodů a ri jim příslušející polohové vektory. Protože souřadnice hmotného středu lze počítat po složkách, platí pro souřadnici xT v naší soustavě:
\[x_\mathrm{T}\,=\,\frac{\sum_{i=1}^2{m_\mathrm{i}x_\mathrm{i}}}{\sum_{i=1}^2{m_\mathrm{i}}}.\tag{1}\]Při dosazení do vztahu (1) dostáváme:
\[x_\mathrm{T}\,=\,\frac{M{\cdot}0\,+\,m{\cdot}a}{M\,+\,m}\,=\,\frac{ma}{81m\,+\,m}\,=\,\frac{a}{82}.\]Číselně:
\[x_\mathrm{T}\,=\,\frac{384\,000}{82}\,\mathrm{km}\,\dot=\,4683\,\mathrm{km}.\]Protože poloměr Země je 6 378 km, představuje vzdálenost xT přibližně 73,4 % tohoto poloměru. Hmotný střed soustavy Země–Měsíc se tedy nachází pod zemským povrchem (vidíme zde nekonzistentnost s obrázkem).
Odpověď
Polohu hmotného středu soustavy Země–Měsíc můžeme v našem souřadném systému popsat těmito souřadnicemi:
\[x_\mathrm{T}\,\dot=\,4683\,\mathrm{km},\] \[y_\mathrm{T}\,=\,0\,\mathrm{km},\] \[z_\mathrm{T}\,=\,0\,\mathrm{km}.\]Hmotný střed soustavy se nachází ve vzdálenosti 0,734-násobku zemského poloměru od středu Země.




