Sbírka řešených úloh

Pohyb částice II

Úloha číslo: 115

• Nápověda 1 pro a): Rovnice trajektorie částice

  Jakými vztahy je popsán pohyb částice ve směrech souřadnicových os x, y, z?

  (Můžete vyjít z vyřešených úkolů v úloze Pohyb částice I.)

  Jak z parametrických rovnic x(t), y(t), z(t) získáte rovnici trajektorie částice?

• Řešení k nápovědě 1

  Pohyb částice je ve směru jednotlivých souřadnicových os popsán vztahy:

  $$x\left(t\right)\,=\,15t^{2}\,,\tag{1}$$ $$y\left(t\right)\,=\,4-20t^{2}\,,\tag{2}$$ $$z\left(t\right)\,=\,0\,.\tag{3}$$

  Trajektorii získáme tak, že z rovnic x(t), y(t), z(t) vyloučíme parametr t.

  Z (1):

  $$t^{2}\,=\,\frac{x}{15}\,.$$

  Dosadíme do (2):

  $$y\,=\,4-\left(\frac{20}{15}\right)x\,=\,4-\left(\frac{4}{3}\right)x\,,$$ $$x\,\geq\,0\,,$$ $$z\,=\,0\,.$$

  Trajektorií je přímka v rovině xy.

• Nápověda 2 pro b): Trajektorie částice

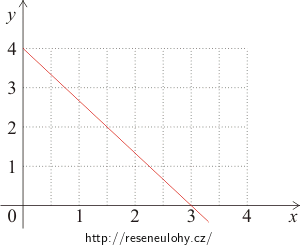
  Je třeba nakreslit přímku popsanou rovnicí $y\,=\,4-\left(\frac{4}{3}\right)x$. Stačí najít dva body, kterými prochází. Zjistěte například, ve kterém bodě protíná osu x a ve kterém osu y.

• Řešení k nápovědě 2

  Průsečík s osou y: x = 0     y = 4.

  Průsečík s osou x:   y = 0     4 = 4x/3     x = 3.

  Přímka prochází body o souřadnicích: [0;4] a [3;0].

   

  Trajektorie částice:

   

  

• Nápověda 3 pro c): Dráha částice v čas. intervalu (t_k1, t_k2)

  Z úlohy Pohyb částice I znáte, jak se s časem mění velikost rychlosti částice:

  $$v\left(t\right)\,=\,50t\,.$$

  Jaký je vztah mezi dráhou částice a velikostí její rychlosti?

  Dráhu vymezte pro časový úsek (t_k1; t_k2).

• Řešení k nápovědě 3

  Dráhu částice vypočítáme z velikosti její rychlosti jako:

   

  $$s\,=\,\int{v\left(t\right)}\mathrm{d}t\,.$$

   

  Pro dráhu částice v časovém intervalu (t_k1, t_k2) platí:

   

  $$s\,=\,\int_{t_\mathrm{k1}}^{t_\mathrm{k2}}{v\left(t\right)}\,\mathrm{d}t\,=\,\int_{t_\mathrm{k1}}^{t_\mathrm{k2}}{50t}\,\mathrm{d}t\,=\,\left[25t^{2}\right]_{t_\mathrm{k1}}^{t_\mathrm{k2}}\,=\,25\left(t_\mathrm{k2}^{2}-t_\mathrm{k1}^{2}\right)\,.$$

• Nápověda 4 pro d): Dráha částice na úseku trajektorie mezi osou x a y

  Můžete vyjít z řešení bodu c) (viz předchozí nápověda). K tomu potřebujete znát ještě časy průchodu částice osami x a y. Tento úkol je řešen v úloze Pohyb částice I.

  Při určení dráhy můžete také vyjít z obrázku trajektorie částice.

• Řešení k nápovědě 4

  $$s\,=\,\int_{t_1}^{t_2}{v(t)}\,\mathrm{d}t\,=\,\int_{t_1}^{t_2}{50t}\,\mathrm{d}t\,=\,\left[25t^{2}\right]_{t_1}^{t_2}\,=\,25\left(t_2^{2}-t_1^{2}\right)$$

  Kde:

  $t_1\,=\,0\,\mathrm{s}\hspace{15px}$je čas průchodu osou y (viz úloha Pohyb částice I)

  $t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}$je čas průchodu osou x (viz úloha Pohyb částice I)

   

  $$s\,=\,25\cdot\left(\frac{1}{\sqrt{5}}\right)^{2}-25{\cdot} 0$$ $$s\,=\,5\,\mathrm{m}$$

   

  Dráhu můžeme určit i z obrázku trajektorie částice:

   

  $$s\,=\,\sqrt{4^{2}+3^{2}}\,\mathrm{m}\,=\,5\,\mathrm{m}\,.$$

• Nápověda 5 pro e): Doba, za kterou částice urazila dráhu na úseku mezi osami x a y

  Uvědomte si, že znáte čas průchodu částice osami x a y.

• Řešení k nápovědě 5:

  Dobu, za kterou částice urazila dráhu na úseku mezi osami x a y, určíme jako:

   

  $$\Delta{t}\,=\,t_2-t_1\,,$$

   

  kde:

  $t_1\,=\,0\,\mathrm{s}\hspace{15px}$je čas průchodu osou y,

  $t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}$je čas průchodu osou x.

   

  Pak platí:

   

  $$\Delta{t}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}-0\,\mathrm{s}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\,.$$

• Nápověda 6 pro f): Průměrná velikost rychlosti na úseku mezi osami x a y

  Jak je definovaná průměrná velikost rychlosti?

  Znáte všechny veličiny, které k výpočtu potřebujete?

• Řešení k nápovědě 6

  Průměrnou velikost rychlosti částice na úseku mezi osami x, y definujeme jako celkovou uraženou dráhu na tomto úseku dělenou celkovou dobou pohybu. Celkovou dráhu i celkovou dobu pohybu na tomto úseku známe z řešení bodu d) a e).

  Tedy:

   

  $$v\,=\,\frac{\Delta{s}}{\Delta{t}}\,=\,\frac{5}{\frac{1}{\sqrt{5}}}\,\mathrm{m\,s^{-1}}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.$$

• Nápověda 7 pro g): Výpočet průměrné velikosti rychlosti částice

  Zkuste, zda můžete průměrnou velikost rychlosti částice vyjádřit jako aritmetický průměr počáteční rychlosti pohybu v₁ a konečné rychlosti pohybu v₂ v případě, kdy velikost rychlosti je lineární funkcí času.

  Lze tento vzorec použít obecně pro jakoukoli funkci velikosti rychlosti v(t)?

• Řešení k nápovědě 7

  Průměrná velikost rychlosti je dána vztahem:

   

  $$v_\mathrm{p}\,=\, \frac{\Delta{s}}{\Delta{t}}\,=\,\frac{ \int_{t_1}^{t_2}{v(t)}\,\mathrm{d}t }{t_2-t_1}\,.$$

   

  V případě, že velikost rychlosti je lineární funkcí času  $v(t)\,=\,k\cdot t$, pak platí:

   

  $$v_\mathrm{p}\,=\,\frac{\int_{t_1}^{t_2}{k.t}\,\mathrm{d}t}{t_2-t_1}\,=\,\frac{\frac{1}{2}kt_2^{2}-\frac{1}{2}kt_1^{2}}{t_2-t_1}\,=\,\frac{\frac{k}{2}\left(t_2+t_1\right)\left(t_2-t_1\right)}{t_2-t_1}\,,$$ $$v_\mathrm{p}\,=\,\frac{k}{2}\left(t_2+t_1\right)\,=\,\frac{v_1+v_2}{2}\,.$$

   

  Uvedený vzorec je platný pro jakoukoli funkci v(t), která je lineární funkcí času.

  Lze ho tedy použít i pro náš konkrétní případ:

   

  $$v_1\,=\,50t_1\,=\,50{\cdot} 0 \,\mathrm{m\,s^{-1}}\,=\, 0\,\mathrm{m\,s^{-1}}\,,$$ $$v_2\,=\,50t_2\,=\,50\cdot \frac{1}{\sqrt{5}} \,\mathrm{m\,s^{-1}}\,=\,\frac{50}{\sqrt{5}}\,\mathrm{m\,s^{-1}}\,=\,10\sqrt{5}\,\mathrm{m\,s^{-1}}\,,$$ $$v_\mathrm{p}\,=\,\frac{\left(v_1+v_2\right)}{2}\,=\,\frac{10\sqrt{5}}{2}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.$$

   

  Pro funkce v(t), které nejsou lineárními funkcemi času, nelze uvedený vztah obecně použít.

• CELKOVÉ ŘEŠENÍ

  Poznámka: Pro přehlednost zápisu nepíšeme ve vztazích jednotky.

   

  Vycházíme z vyřešených úkolů z úlohy Pohyb částice I:

  a)

  Pohyb částice je ve směru jednotlivých souřadnicových os popsán vztahy:

  $$x(t)\,=\,15t^{2}\,,\tag{1}$$ $$y(t)\,=\,4-20t^{2}\,,\tag{2}$$ $$z(t)\,=\,0\,.\tag{3}$$

  Trajektorii získáme tak, že z rovnic x(t), y(t), z(t) vyloučíme parametr t.

  Z (1):

  $$t^{2}\,=\,\frac{x}{15}\,.$$

  Dosadíme do (2):

  $$y\,=\,4-(\frac{20}{15})x\,=\,4-(\frac{4}{3})x\,,$$ $$x\,\geq\,0\,,$$ $$z\,=\,0\,.$$

   

  b)

  Průsečík přímky s osou y:   x = 0;     y = 4

  Průsečík přímky s osou x:   y = 0;     4 = 4x/3     x = 3

  Přímka prochází body o souřadnicích: [0;4] a [3;0].

   

  Trajektorie částice:

   

  

   

  c)

  Dráhu částice vypočítáme z velikosti její rychlosti jako:

   

  $$s\,=\,\int{v\left(t\right)}\mathrm{d}t\,.$$

   

  Pro dráhu částice v časovém intervalu (t_k1, t_k2) platí:

   

  $$s\,=\,\int_{t_\mathrm{k1}}^{t_\mathrm{k2}}{v(t)}\,\mathrm{d}t\,=\,\int_{t_\mathrm{k1}}^{t_\mathrm{k2}}{50t}\,\mathrm{d}t\,=\,\left[25t^{2}\right]_{t_\mathrm{k1}}^{t_\mathrm{k2}}\,=\,25\left(t_\mathrm{k2}^{2}-t_\mathrm{k1}^{2}\right).$$

   

  d)

  Můžeme vyjít z řešení bodu c). K tomu potřebujeme znát ještě časy průchodu částice osami x a y.

  $$s\,=\,\int_{t_1}^{t_2}{v\left(t\right)}\,\mathrm{d}t\,=\,\int_{t_1}^{t_2}{50t}\,\mathrm{d}t\,=\,\left[25t^{2}\right]_{t_1}^{t_2}\,=\,25\left(t_2^{2}-t_1^{2}\right)\,,$$

  kde:

  $t_1\,=\,0\,\mathrm{s}\hspace{15px}$je čas průchodu osou y (viz úloha Pohyb částice I),

  $t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}$je čas průchodu osou x (viz úloha Pohyb částice I),

   

  $$s\,=\,25\cdot(\frac{1}{\sqrt{5}})^{2}-25{\cdot}0\,,$$ $$s\,=\,5\,\mathrm{m}\,.$$

   

  Dráhu můžeme určit i z obrázku trajektorie částice:

   

  $$s\,=\,\sqrt{4^{2}+3^{2}}\,\mathrm{m}\,=\,5\,\mathrm{m}\,.$$

   

  e)

  Dobu, za kterou částice urazila dráhu na úseku mezi osami x a y, určíme jako:

   

  $$\Delta{t}\,=\,t_2-t_1\,,$$

   

  kde:

  $t_1\,=\,0\,\mathrm{s}\hspace{15px}$je čas průchodu osou y,

  $t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}$je čas průchodu osou x.

   

  Pak platí:

   

  $$\Delta{t}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}-0\,\mathrm{s}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\,.$$

   

  f)

  Průměrnou velikost rychlosti částice na úseku mezi osami x, y definujeme jako celkovou uraženou dráhu na tomto úseku dělenou celkovou dobou pohybu. Celkovou dráhu i celkovou dobu pohybu na tomto úseku známe z řešení bodu d) a e).

  Tedy:

   

  $$v\,=\,\frac{\Delta{s}}{\Delta{t}}\,=\,\frac{5}{\frac{1}{\sqrt{5}}}\,\mathrm{m\,s^{-1}}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.$$

   

  g)

  Průměrná velikost rychlosti je dána vztahem:

   

  $$v_\mathrm{p}\,=\,\frac{\Delta{s}}{\Delta{t}}\,=\,\frac{ \int_{t_1}^{t_2}{v(t)}\,\mathrm{d}t }{t_2-t_1}\,.$$

   

  V případě, že velikost rychlosti je lineární funkcí času  $v\left(t\right)\,=\,k\cdot t$, pak platí:

   

  $$v_\mathrm{p}\,=\,\frac{\int_{t_1}^{t_2}{k.t}\,dt}{t_2-t_1}\,=\,\frac{\frac{1}{2}kt_2^{2}-\frac{1}{2}kt_1^{2}}{t_2-t_1}\,=\,\frac{\frac{k}{2}(t_2+t_1)(t_2-t_1)}{t_2-t_1}\,,$$ $$v_\mathrm{p}\,=\,\frac{k}{2}(t_2+t_1)\,=\,\frac{v_1+v_2}{2}\,.$$

   

  Uvedený vzorec je tedy obecně platný pro jakoukoli funkci v(t), která je lineární funkcí času.

  Lze ho tedy použít i pro náš konkrétní případ:

   

  $$v_1\,=\,50t_1\,=\,50{\cdot} 0 \,\mathrm{m\,s^{-1}}\,=\, 0\,\mathrm{m\,s^{-1}}\,,$$ $$v_2\,=\, 50t_2\,=\,50\cdot \frac{1}{\sqrt{5}} \,\mathrm{m\,s^{-1}}\,=\,\frac{50}{\sqrt{5}}\,\mathrm{m\,s^{-1}}\,=\,10\sqrt{5}\,\mathrm{m\,s^{-1}}\,,$$ $$v_\mathrm{p}\,=\,\frac{(v_1+v_2)}{2}\,=\,\frac{10\sqrt{5}}{2}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.$$

• Odpověď

  a)

  Rovnice trajektorie pohybu částice:

  $$y\,=\,4-\left(\frac{4}{3}\right)x\,,$$ $$x\,\geq\,0\,,$$ $$z\,=\,0\,.$$

  Trajektorií je přímka v rovině xy.

   

  b)

  

   

  c)

  $$s\,=\,25\left(t_\mathrm{k2}^{2}-t_\mathrm{k1}^{2}\right)\,.$$

  d)

  $$s\,=\,25\left(t_2^{2}-t_1^{2}\right)\,=\,5\,\mathrm{m}\,,$$

  kde:

  $t_1\,=\,0\,\mathrm{s}\hspace{15px}$čas průchodu osou y,

  $t_2\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\hspace{15px}$je čas průchodu osou x.

   

  Nebo z obrázku trajektorie:

  $$s\,=\,\sqrt{4^{2}+3^{2}}\,\mathrm{m}\,=\,5\,\mathrm{m}\,.$$

  e)

  $$\Delta{t}\,=\,t_2-t_1\,,$$ $$\Delta{t}\,=\,\frac{1}{\sqrt{5}}\,\mathrm{s}\,.$$

  f)

  $$v\,=\,\frac{\Delta{s}}{\Delta{t}}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,,$$

  g)

  Uvedený vzorec je obecně platný pro jakoukoli funkci v, která je lineární funkcí času.

  Pro náš případ lze tedy uvedený vztah použít:

  $$v_\mathrm{p}\,=\,\frac{(v_1+v_2)}{2}\,=\,5\sqrt{5}\,\mathrm{m\,s^{-1}}\,.$$