Změna objemu železné tyče
Úloha číslo: 2150
Jak se změní objem železné tyče tvaru hranolu s rozměry 1 m a dvakrát 0,1 m, když je tyč ve směru svého největšího rozměru namáhaná tahem 10 kN/cm2? Modul pružnosti železa, z něhož je tyč zhotovena, je 200 GPa a modul pružnosti ve smyku je 75 GPa.
Zápis
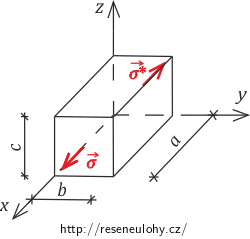
a = 100 cm, b = c = 10 cm rozměry železné tyče σ = 10 kN·cm−2 tah ve směru rozměru a E = 200 GPa modul pružnosti železa v tahu G = 75 GPa modul pružnosti železa ve smyku ΔV = ? změna objemu Rozbor
Relativní změna objemu je součtem všech relativních změn rozměrů tyče. Ve směrech, kde nepůsobí napětí, jsou deformace stejné a deformaci pro směr rozměru namáhaného tahem lze určit pomocí Hookova zákona. Poměr deformace ve směru působícího napětí a deformace v jiném směru lze vyjádřit pomocí vztahu závislého na modulu pružnosti v tahu a modulu pružnosti ve smyku.
Nápověda
Vyjádřete relativní objemovou deformaci jako součet relativních deformací, kde každá odpovídá určitému rozměru tyče. Relativní deformace ve směrech, kde nepůsobí tahové napětí, uvažujte stejné. Použijte vztah pro Poissonovo číslo v závislosti na modulu v tahu a modulu ve smyku. Relativní objemovou deformaci vyjádřete závislou pouze na deformaci ve směru působícího napětí. Deformaci ve směru namáhaného tahem vyjádřete pomocí napětí a modulu v tahu.
Řešení
Pro změnu objemu platí vztah:
\[\Delta V\,=\,\left(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}\right)V_0.\tag{1}\]Když budeme uvažovat, že tyč je namáhaná v tahu ve směru x, pak můžeme uvažovat deformace v ostatních směrech jako rovnocenné, tedy:
\[\varepsilon_{yy}=\varepsilon_{zz}.\tag{2}\]Poznámka: Vztah (2) platí pro izotropní materiály, obecněji už to tak jednoduché není.
Pomocí (2) můžeme (1) upravit na:
\[\Delta V\,=\,\left(\varepsilon_{xx}+2\varepsilon_{yy}\right)V_0.\tag{3}\]Jelikož máme zadaný modul pružnosti v tahu E a smykový modul pružnosti G, bude se zde hodit vztah:
\[\frac{\varepsilon_{xx}}{\varepsilon_{yy}}\,=\,\frac{2G}{2G-E}.\tag{4}\]Vztah (4) vychází z toho, že poměr deformací v podélném a příčném směru je roven záporné hodnotě Poissonovy konstanty. Její vyjádření pomocí modulů pružnosti v tahu a ve smyku lze nalézt v úloze Poissonova konstanta.
Z (4) vyjádříme:
\[\varepsilon_{yy}\,=\,\frac{2G-E}{2G}\varepsilon_{xx}.\tag{5}\]Když (5) dosadíme do (3), potom dostáváme:
\[\Delta V\,=\,\left(\varepsilon_{xx}+\frac{2G-E}{G}\varepsilon_{xx}\right)V_0\,=\,\left(\frac{3G-E}{G}\right)\varepsilon_{xx} V_0.\tag{6}\]Máme zadáno napětí, takže se nám bude hodit ještě vztah:
\[\varepsilon_{xx}\,=\,\frac{\sigma_{xx}}{E}.\tag{7}\]Teď už pro hledaný vztah stačí dosadit (7) do (6):
\[\Delta V\,=\,\left(\frac{3G-E}{G E}\right)\sigma_{xx} V_0.\tag{8}\]Dále už stačí jenom číselně dosadit, tedy:
\[\Delta V\,=\,\left(\frac{3·75·10^{5}-200·10^{5}}{75·10^{5}·200·10^{5}}\right)·10^{4}·100·10·10 \mathrm{cm^{3}}\,=\,1{,}67 \mathrm{cm^{3}}.\]Odpověď
Objem železné tyče se změní o:
\[\Delta V\,=\,1{,}67 \mathrm{cm^{3}}.\]

