Myš a kočka
Úloha číslo: 107
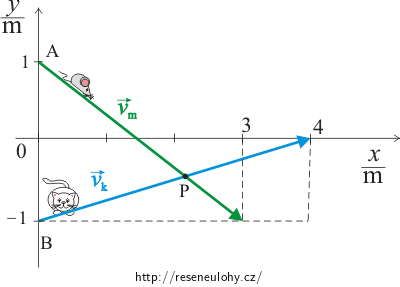
Myš se pohybuje rovnoměrně přímočaře z bodu A = [0; 1] m rychlostí \(\vec{v}_\mathrm{m}\,=\,(3;\,-2)\,\mathrm{m\cdot s^{-1}}\) a kočka rovnoměrně přímočaře z bodu B = [0; −1] m rychlostí \(\vec{v}_\mathrm{k}\,=\,(4;\,1)\,\mathrm{m\cdot s^{-1}}\).
a) Určete místo, kde se jejich cesty protnou. Setkají se zde?
b) Určete čas, kdy jsou si kočka a myš nejblíže.
c) Určete nejmenší vzdálenost kočky a myši.
Poznámka: Parametrické rovnice by měly být zapsány ve tvaru např.:
Pro zjednodušení zápisu jednotky ve vztazích nepíšeme.
Nápověda 1 pro a): Průsečík cest kočky a myši
Do souřadného systému vyznačte počáteční polohu kočky a myši. Dokážete nakreslit přímky, po kterých se pohybují, když znáte směry jejich rychlostí? Pokud jste rýsovali přesně, průsečík přímek snadno odečtete z obrázku.
Průsečík můžete také spočítat, pokud si napíšete rovnice přímek, po kterých se kočka a myš pohybují. U každé znáte jeden bod, kterým prochází, a směrnici.
Nápověda 2 pro a): Setkání kočky a myši
Za jakou dobu dorazí do bodu P myš a za jakou kočka? Je čas stejný?
Nápověda 3: Závislost vzdálenosti kočky a myši na čase
Víte, jak se s časem mění souřadnice kočky a myši. Dokážete vyjádřit, jak se s časem mění jejich vzdálenost? Vztah pro výpočet vzdáleností dvou bodů snadno odvodíte z obrázku nebo se podívejte do tabulek.
Nápověda 4 pro b): Čas, kdy jsou si myš a kočka nejblíže
Víte, jak se s časem mění vzdálenost kočky a myši. Jak najdete minimum této funkce?
Nápověda 5 pro c): Nejmenší vzdálenost kočky a myši
Znáte čas, kdy jsou si kočka s myší nejblíže i jak se mění s časem jejich vzdálenost. Jak určíte nejmenší vzdálenost?
CELKOVÉ ŘEŠENÍ
a)
Grafické řešení:
Obrázek 1:
\[A\,=\,[0;\,1]\,\mathrm{m}\] \[v_\mathrm{m}\,=\,(3;\,-2)\,\mathrm{m\cdot s^{-1}}\] \[B\,=\,[0;\,-1]\,\mathrm{m}\] \[v_\mathrm{k}\,=\,(4;\,1)\,\mathrm{m\cdot s^{-1}}\] Početní řešení:
Parametrické rovnice přímky, po které se pohybuje myš:
\[x_\mathrm{m}\,=\,0+3t_\mathrm{m}\,,\] \[y_\mathrm{m}\,=\,1\,-\,2t_\mathrm{m}\,.\]Vyloučením parametru tm získáme rovnici trajektorie, po které se pohybuje myš:
\[t_\mathrm{m}\,=\,\frac{x_\mathrm{m}}{3}\,.\]Trajektorie pro myš:
\[y_\mathrm{m}\,=\,1\,-\,2\frac{x_\mathrm{m}}{3}\,,\] \[3y_\mathrm{m}\,=\,3\,-\,2x_\mathrm{m}\,.\]Parametrické rovnice přímky, po které se pohybuje kočka:
\[x_\mathrm{k}\,=\,0\,+\,4t_\mathrm{k}\,,\] \[y_\mathrm{k}\,=\,-1\,+\,t_\mathrm{k}\,.\]Vyloučením parametru tk získáme rovnici trajektorie, po které se pohybuje kočka:
\[t_\mathrm{k}\,=\,\frac{x_\mathrm{k}}{4}\,.\]Trajektorie pro kočku:
\[y_\mathrm{k}\,=\,-1\,+\,\frac{x_\mathrm{k}}{4}\,,\] \[4y_\mathrm{k}\,=\,x_\mathrm{k}\,-\,4\,.\]Průsečík trajektorií:
\[x_\mathrm{m} \,=\, x_\mathrm{k} \,=\, x\,,\] \[y_\mathrm{m} \,=\, y_\mathrm{k} \,=\, y\,.\]Řešíme soustavu dvou rovnic o dvou neznámých x, y:
\[3y \,=\, 3\,-\,2x\,,\tag{1}\] \[4y \,=\, x\,-\,4\,.\tag{2}\]Z (2):
\[x \,=\, 4y \,+\, 4\,.\]Dosadíme do (1):
\[3y \,=\, 3 \,-\, 8y \,-\, 8\,.\]Odtud:
\[y\,=\,-\frac{5}{11}\,,\] \[x\,=\,\frac{24}{11}\,.\]Souřadnice průsečíku P:
\[P \,=\, \left[\frac{24}{11};\,-\frac{5}{11}\right]\,\mathrm{m}\,.\]Myš se v bodě P
\[\left[\frac{24}{11};\,-\frac{5}{11}\right]\,\mathrm{m}\]ocitne v čase
\[t_\mathrm{m} \,=\, \frac{x}{3}\ \,=\, \frac{24}{11{\cdot}3}\ \,\mathrm{s} \,=\, \frac{8}{11}\,\mathrm{s}\,.\]Kočka se v bodě P
\[\left[\frac{24}{11};\,-\frac{5}{11}\right]\,\mathrm{m}\]ocitne v čase
\[t_\mathrm{k}\, =\, \frac{x}{4}\ \,=\, \frac{24}{11{\cdot}4}\ \,\mathrm{s}= \frac{6}{11}\,\mathrm{s}\,.\]Časy jsou různé, to znamená, že se v tomto bodě nesetkají.
b)
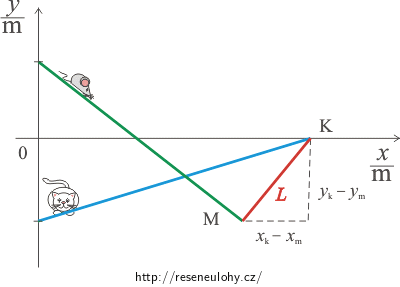
Závislost vzdálenosti kočky a myši na čase L(t) můžeme odvodit z obrázku.
Obrázek 2:
\[x_\mathrm{k}\,-\,x_\mathrm{m}\,=\,4t\,-\,3t\,=\,t\] \[y_\mathrm{k}\,-\,y_\mathrm{m}\,=\,t-1\,+\,2t-1\,=\,3t-2\]Z Pythagorovy věty:
\[L(t)\,=\,\sqrt{(x_\mathrm{k}\,-\,x_\mathrm{m})^{2}+(y_\mathrm{k}\,-\,y_\mathrm{m})^{2}}=\sqrt{10t^{2}\,-12t\,+\,4}\,.\]Najít čas, kdy jsou si kočka a myš nejblíže, znamená najít minimum funkce L(t).
Zderivujeme funkci L(t) podle času t a zjistíme extrém:
\[\frac{\mathrm{d}L}{\mathrm{d}t}\,=\,\frac{1}{2}\,\frac{20t_\mathrm{min}\,-12}{\sqrt{10t_\mathrm{min}^{2}\,-12t_\mathrm{min}\,+4}}\,=\,0\,,\] \[20t_\mathrm{min}\,-\,12 \,=\, 0\,,\] \[t_\mathrm{min}\,=\,\frac{3}{5}\,\mathrm{s}\,.\]Tedy čas, kdy jsou si myš a kočka nejblíže, je:
\[t_\mathrm{min} \,=\, 0{,}6\,\mathrm{s}\,.\]c)
Čas, kdy jsou si myš a kočka nejblíže, je:
\[t_\mathrm{min}\,=\, 0{,}6 \,\mathrm{s}\,.\]Po dosazení této hodnoty do funkce L(t) získáme nejmenší vzdálenost myši a kočky:
\[L_\mathrm{min} \,=\,\sqrt{10t_\mathrm{min}^{2}-12t_\mathrm{min}\,+\,4}\,, \] \[L_\mathrm{min} \,=\, \sqrt{10{\cdot} 0{,}6^{2}\,-12{\cdot}0{,}6\,+4}\,\mathrm{m}\,=\,\sqrt{0{,}4}\,\mathrm{m} \,=\, 0{,}63 \,\mathrm{m}\,. \]Odpověď
a) Cesty myši a kočky se protnou v bodě:
\[P \,=\, \left[\frac{24}{11};\,-\frac{5}{11}\right]\,\mathrm{m}\,.\]Myš a kočka se v bodě P nesetkají, protože myš se v tomto bodě ocitne v čase
\[t_\mathrm{m}\,=\,\frac{8}{11}\,\mathrm{s}\]a kočka se v tomto bodě ocitne v čase
\[t_\mathrm{k}\,=\,\frac{6}{11}\,\mathrm{s}\,.\]b) Čas, kdy jsou si myš a kočka nejblíže, je:
\[t_\mathrm{min} \,=\, 0{,}6 \,\mathrm{s}\,.\]c) Nejmenší vzdálenost myši a kočky je:
\[L_\mathrm{min}\, =\, \sqrt{10t_\mathrm{min}^{2}\,-\,12t_\mathrm{min}\,+\,4} \,=\, 0{,}63\,\mathrm{m}\,.\]Vizualizace pohybu
Následující aplet slouží k vizualizaci pohybu myši a kočky. Zelený bod M reprezentuje polohu myši a modrý bod K reprezentuje polohu kočky. Kliknutím na tlačítko „Zapnout animaci“ se spustí animace, opětovné kliknutí tuto animaci zastaví. Čas \(t\) je možné měnit na posuvníku. Tlačítko „Zapnout stopu“ zapíná/vypíná stopu bodů M a K. Po zaškrtnutí tlačítka „Zobrazit trajektorie“ se zobrazí trajektorie pro myš i kočku bez nutnosti vykreslení pomocí stop bodů M a K. Zaškrtnutí talčítka „Zobrazit závislost \(L(t)\)“ vykreslí graf závislosti vzdálenosti kočky a myši \(L\) na čase \(t\). Tlačítko „Reset“ zastaví animaci a vrátí aplet do původního stavu.
Z apletu je dobře vidět, že kočka myš skutečně nechytila, i když se protínají jejich trajektorie. Z grafu můžeme jednoduše odečíst čas, kdy byla vzdálenost mezi kočkou a myší nejmenší.