Vodní nádrž Orlík
Úloha číslo: 666
Vodní nádrž Orlík je největší českou přehradou co do objemu zadržované vody. Pata hráze leží v nadmořské výšce 275 m n. m., maximální povolená kóta hladiny v nádrži je 354 m n. m. Plocha vodní nádrže je přibližně 2730 ha.
a) Během povodní v roce 2002 byla maximální povolená výška hladiny překročena o 2 m. Určete, jak velký byl tlak na dně u paty hráze.
b) V době kulminace Vltavy byl přítok do nádrže 4400 m3/s, odtok z nádrže 3100 m3/s. Určete, za jak dlouho by v této situaci stoupla hladina v nádrži o 1 m. (Uvažujte, že zvýšení hladiny nezmění plochu nádrže.)

Zápis
h0 = 2 m výška, o kterou byla překročena maximální kóta hladiny h1 = 354 m n. m. nadmořská výška kóty hladiny h2 = 275 m n. m. nadmořská výška dna u paty hráze S = 2730 ha = 27 300 000 m2 plocha vodní nádrže h´ = 1 m přírůstek výšky hladiny v nádrži p = ? výsledný hledaný tlak Z tabulek: g = 10 N/kg číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu ρ = 1000 kg/m3 hustota vody pa = 101,325 kPa normální atmosférický tlak Nápověda 1 – k úkolu a)
Jak velký bude výsledný tlak na dně nádrže, o který se zajímáme? Co vše se na něm podílí?
Nápověda 2 – k úkolu a)
Jak velký je přibližně atmosférický tlak?
Nápověda 3 – k úkolu a)
Jak se spočítá hydrostatický tlak? Jaká byla v době povodní maximální hloubka přehrady u hráze?
Nápověda 4 – k úkolu a)
Dosaďte do vztahu (1) ze vztahů (2) a (3) a vypočítejte celkový tlak p.
Nápověda 5 – k úkolu b)
Jaký přírůstek objemu v nádrži znamená zvýšení hladiny o h´ = 1 m?
Situace je znázorněna na následujícím obrázku:
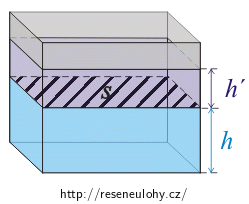
Nápověda 6 – k úkolu b)
Kolik metrů krychlových vody přibude v nádrži za sekundu? Jak dlouho tedy potrvá, než přibude objem V? (Nešlo by to třeba trojčlenkou?)
Celkové řešení
Část a):
Absolutní tlak nepřepočítaný na hladinu moře, který je na dně nádrže, je součtem atmosférického tlaku pa a hydrostatického tlaku ph:
\[p\,=\,p_\mathrm{a}\,+\,p_\mathrm{h}\,.\tag{1}\]Atmosférický tlak je vyvolán tíhou vzduchového sloupce nad hladinou nádrže, hydrostatický tlak tíhou vodního sloupce nade dnem nádrže.
Hodnota tzv. normálního atmosférického tlaku je stanovena jako:
\[p_\mathrm{a}\,=\,101{,}325\,\mathrm{kPa}\,=\,101325\,\mathrm{Pa}\,.\tag{2}\]
Pro náš výpočet postačí uvažovat přibližnou hodnotu 100 000 Pa.
Pro hydrostatický tlak platí vztah:
\[p_\mathrm{h}\,=\,h{\rho}g\,,\tag{3}\]
kde h je hloubka přehrady, \({\rho}\) hustota kapaliny a g = 10 N/kg (číslo, kterým musíme vynásobit hmotnost, abychom dostali příslušnou gravitační sílu).
Maximální hloubku určíme z rozdílu nadmořských výšek a přičtením přebytku 2 m jako:
\[h\,=\,((h_{1}\,-\,h_2)\,+\,h_0)\,=\,((354\,-\,275)\,+\,2)\,\mathrm{m}\,=\,81\,\mathrm{m}\,.\tag{4}\]
Spojením vztahů (1), (2), (3) a (4) dostáváme:
\(p\,=\,p_\mathrm{a}\,+\,((h_{1}\,-\,h_2)\,+\,h_0){\rho}g\,,\)
\(p=(100 000\,+\,((354\,-\,275)\,+2\,){\cdot}1000{\cdot}10)\,\mathrm{Pa}\,=\,910 000\,\mathrm{Pa}\,,\)
\(p=910\,\mathrm{kPa}\,.\)
Tlak na dně nádrže u paty hráze byl asi 910 kPa.
Část b):
Situace je znázorněna na následujícím obrázku:

Stoupne-li hladina o h´, přibude v nádrži voda o objemu:
V = S·h´.
Příklad řešíme dále trojčlenkou:
Za 1 sekundu přibude v nádrži (4400−3100) m3 vody, tedy:
1 s... 1300 m3,
x s... S·h´.
Odtud:
\[x\,=\,\frac{S{\cdot}h'{\cdot}1}{1300}\,\mathrm{s}\,=\,(\frac{27300000{\cdot}1{\cdot}1}{1300})\,\mathrm{s}\,=\,21000\,s\,\dot=\,5{,}8\,\mathrm{h}\,.\]
Při zadaném přítoku a odtoku by stoupla hladina nádrže o 1 m za přibližně 5,8 hodin.
Odpověď
a) \(p\,=\,p_\mathrm{a}\,+\,((h_{1}\,-\,h_2)\,+\,h_0){\rho}g = 910 \,\mathrm{kPa}\)
Na dně u paty hráze byl tlak asi 910 kPa.
b) \(x\,=\,\frac{S{\cdot}h'{\cdot}1}{1300}\,\mathrm{s}\,\dot=\,5{,}8\,\mathrm{h}\)
Při zadaném přítoku a odtoku by stoupla hladina nádrže o 1 m za přibližně 5,8 hodin.






