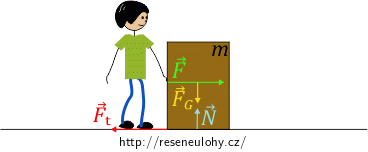Posouvání bedny
Úloha číslo: 2212
Chlapec tlačí vodorovným směrem do bedny o hmotnosti \(30\,\mathrm{kg}\). Působí na ni přitom silou \(90\,\mathrm{N}\). Koeficient statického tření mezi bednou a vodorovnou podlahou je 0,37. (Počítejte s \(g = 10\,\mathrm{m\cdot s^{-2}}\).)
a) Jaká je za této situace maximální velikost klidové třecí síly?
b) Pohne se bedna?
c) Jak velkou třecí silou působí podlaha na bednu?
Druhý chlapec chce pomoci a táhne bednu svisle vzhůru.
d) Jakou nejmenší tahovou silou musí na bednu působit, aby se prvnímu chlapci podařilo uvést ji do pohybu? (První chlapec stále tlačí silou \(90\,\mathrm{N}\).)
e) Jakou nejmenší silou by musel na bednu působit druhý chlapec, kdyby ji místo zvedání tahal vodorovným směrem, aby se oběma podařilo bednu posunout?
Bedna nyní leží na desce. Koeficient statického tření je stejný: 0,37.
f) O jaký minimální úhel musí chlapec zvednout desku, aby bedna začala sjíždět?
g) Jaký je koeficient dynamického tření mezi bednou a deskou, jestliže sjede za \(3\,\mathrm{s}\) o \(2\,\mathrm{m}\)?
Zápis úlohy
Označme:
\(m=30\,\mathrm {kg}\)…hmotnost bedny
\(F = 90\,\mathrm {N}\)…síla, kterou působí chlapec ve vodorovném směru
\(f =0{,}37 \)…koeficient statického tření mezi bednou a podlahou
\(g = 10\,\mathrm {m\cdot s^{-2}}\)…tíhové zrychlení
Obrázek situace
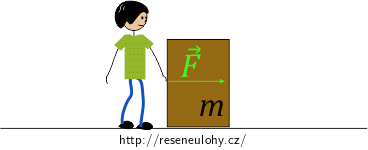
Rozbor
V první části úlohy budeme hodně pracovat s pojmem statické (též klidové) třecí síly. Je důležité si uvědomit, jakých hodnot může klidová třecí síla dosahovat a jak určíme její maximální velikost. Bedna v prvních případech leží na vodorovné podlaze, tíhová síla tak působí kolmo k podložce.
Pro každou situaci je dobré si nakreslit obrázek a do něj vyznačit působící síly. Často budeme řešit mezní případy, určovat nejmenší či největší sílu. K jejich určení budeme využívat rovnovážného stavu tělesa, kdy je výslednice sil působících na bednu nulová.
V poslední části úlohy se dostaneme od případu na vodorovné podlaze k nakloněné rovině. Opět nakreslíme obrázek a vyznačíme síly působící na bednu. Při určování úhlu sklonu pro rozjetí bedny budeme uvažovat hraniční situaci, kdy klidová třecí síla dosáhne maximální hodnoty. V situaci, kdy bedna sjíždí, si musíme uvědomit, že mezi ní a deskou bude působit již ne klidová, ale smyková třecí síla a že koeficient statického tření je větší než u smykového tření. Rozmyslíme, jaká bude v této situaci výslednice sil a jakým pohybem se bude bedna pohybovat.
Nápověda a)–c)
Rozmyslete si, jaké síly působí na bednu v situaci, kdy na ni tlačíme, ale ještě se nerozjela a je v klidu, a nakreslete si je do obrázku. Jaká je v této situaci výslednice sil a jak velká musí být klidová třecí síla?
Pak si připomeňte vztah pro maximální hodnotu klidové třecí síly. Jak velkou silou musíme alespoň tlačit, aby se bedna pohnula?
Řešení a)
Maximální velikost klidové třecí síly \(F_\mathrm{t_{max}}\) určíme obecně jako
\[F_\mathrm{t_{max}} =Nf,\tag{1}\]
kde \(N\) je kolmá tlaková síla, kterou bedna tlačí do podložky, a \(f\) koeficient statického tření. V našem případě tedy:
\[F_\mathrm{t_{max}} = mg f.\]
Číselně:
\[F_\mathrm{tmax} = 30 {\cdot} 10 \cdot 0{,}37\,\mathrm N = 111\,\mathrm N\]
Řešení b)
V předchozí části úlohy jsme zjistili, jaká je maximální klidová třecí síla, resp. její velikost. Co přesně nám tento výsledek říká? Dokud budeme působit silou menší nebo rovnou velikosti \(F_\mathrm{t_{max}}\), bedna se nepohne. Působíme-li větší silou, bedna se pohne.
Chlapec na bednu působí silou \(F = 90\,\mathrm N\) a velikost maximální klidové třecí síly je \(F_\mathrm{t_{max}} = 111\,\mathrm N\). Platí:
\[F_\mathrm{t_{max}}>F.\]
Chlapec nepůsobí dostatečně velkou silou, proto se bedna nepohne.
Řešení c)
Bedna zůstává v klidu, výslednice sil na ni působících musí být tedy nulová. Klidová třecí síla podlahy působící na bednu musí vyrovnávat sílu, kterou chlapec bednu tlačí.
Platí tedy:
\[ F_\mathrm{t}=F=90\,\mathrm{N}. \]
Nápověda d)
Zkuste se nejprve zamyslet, co druhý chlapec vlastně dělá, tahá-li bednu svisle vzhůru. Pak zjistěte, jak těžkou bednu by první chlapec dokázal roztlačit sám. Sílu, kterou je třeba táhnout vzhůru, pak již snadno dopočítáte.
Řešení d)
Aby první chlapec bednu roztlačil, musí na ni působit silou alespoň o velikosti maximální klidové třecí síly bedny. Tato síla závisí na kolmé tlakové síle, kterou bedna tlačí do podložky. Nejprve zjistíme, jakou největší hmotnost by mohla bedna za daných okolností mít, aby ji první chlapec dokázal silou \(90\,\mathrm{N}\) roztlačit. Tuto hmotnost \(m_\mathrm{max}\) snadno určíme podle (1), kde za sílu \(F_\mathrm{t}\) budeme považovat sílu \(F\), kterou působí první chlapec na bednu. Bedna se stále nachází na vodorovné podložce, tedy pro sílu \(\vec N\) můžeme udělat stejný závěr jako v předchozích částech úlohy.
Máme tedy rovnici
\[F=m_\mathrm{max}gf.\]
Vyjádříme neznámou \(m_\mathrm{max}\), dosadíme a dopočteme:
\[m_\mathrm{max}=\frac{F}{gf},\]
\[m_\mathrm{max}=\frac{90}{10{\cdot} 0{,}37}\,\mathrm {kg} \,\dot=\, 24{,}3\,\mathrm{kg}.\]
První chlapec je schopen roztlačit bednu o hmotnosti \(m_\mathrm{max}\). Druhý chlapec působí na bednu silou svisle vzhůru, tedy bednu nadlehčuje. O kolik ji musí nadzvednout? Chlapec musí bednu odlehčit právě tak, aby část „zbývající“ hmotnosti byl první chlapec schopen roztlačit. To znamená, že
\[ m-m_\mathrm{max}\,\dot=\,(30-24{,}3)\,\mathrm{kg}\,\dot=\,5{,}7\,\mathrm {kg} \]
je hmotnost, kterou zvedá druhý chlapec. Podle druhého Newtonova zákona pak pro velikost síly \(F_2\), kterou působí druhý chlapec, platí:
\[F_2\,\dot=\,5{,}7{\cdot} 10\,\mathrm N\,\dot=\, 57\,\mathrm N.\]
Druhý chlapec musí na začátku zatáhnout o maličko větší silou než 57 N, aby se bedna rozjela.Nápověda e)
Víte již, jak velká je maximální klidová třecí síla mezi bednou a podlahou. Jak velkou silou je třeba zatlačit, aby se bedna rozjela? Jak velkou silou musí tedy zapůsobit druhý chlapec?
Řešení e)
Bedna se začne pohybovat, pokud celková síla, kterou oba chlapci ve vodorovném směru působí, vyrovná klidovou třecí sílu a o trochu ji překročí. Dostaneme jednoduchou rovnici pro hraniční podmínku, kde je nyní \(F_2\) velikost síly, kterou působí druhý chlapec vodorovně:
\[F + F_2 = F_\mathrm{tmax}.\]
Z rovnice snadno vyjádříme neznámou \(F_2\) a dosadíme:
\[F_2= (111−90)\,\mathrm{N}=21\,\mathrm{N}.\]
Druhý chlapec musí na začátku zatáhnout o maličko větší silou než 21 N, aby se bedna rozjela.
Nápověda f)
Nakreslete si obrázek bedny na nakloněné desce a vyznačte všechny síly, které na bednu působí. Rozmyslete, která síla či její složka bude teď odpovědná za rozpohybování bedny a která síla tomu naopak brání. Uvědomte si, co bude platit pro jejich velikosti těsně před rozjetím bedny.
Řešení f)
Bedna již neleží na vodorovné podlaze, ale je umístěna na nakloněné desce. Úhel, o který musí chlapec desku s bednou zvednout, označme \(\alpha\).
Nakresleme si nový obrázek situace s vyznačenými silami, které na bednu působí.
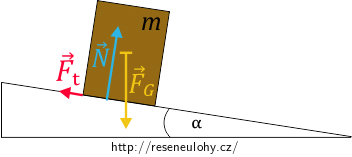
\(\vec {F_\mathrm{G}}\) je tíhová síla, \(\vec {F_\mathrm{t}}\) klidová třecí síla a \(\vec {N}\) síla, kterou tlačí do bedny deska. Abychom se silami mohli lépe pracovat, rozložíme ještě \(\vec {F_\mathrm{G}}\) do kolmých směrů podle os x a y na následujícím obrázku.
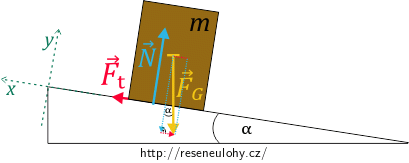
Jak chlapec desku zvedá, zvětšuje se x-ová složka tíhové síly. Klidová třecí síla ji dorovnává až do okamžiku, kdy dosáhne své maximální hodnoty. Při dalším zvýšení sklonu desky se bedna rozjede. Hledejme tedy mezní případ, tj. kdy nastane rovnováha těchto sil.
Jestliže je bedna v klidu, musí být výslednice sil nulová. Platí tedy:
\[F_\mathrm{t}=F_{\mathrm{G}_x},\tag{2}\]
\[N=F_{\mathrm{G}_y}.\tag{3}\]
Z obrázku dokážeme určit velikost sil \(F_\mathrm{Gx}\) a \(F_\mathrm{Gy}\) v závislosti na neznámém úhlu \(\alpha\). S využitím pravoúhlého trojúhelníku a goniometrických funkcí dostaneme:
\[F_{\mathrm{G}_x}=F_\mathrm{G} \sin{\alpha},\tag{4}\]
\[F_{\mathrm{G}_y}=F_\mathrm{G} \cos{\alpha}.\tag{5}\]
Maximální velikost třecí síly umíme vyjádřit podle (1). Tentokrát ovšem pro sílu \(N\) neplatí, že ji můžeme nahradit silou tíhovou. Síla kolmá na podložku je podle (3) rovna pouze jedné její složce. Pokud dosadíme do (2) podle získaných vztahů (4) a (5), dostaneme:
\[fmg\cos{\alpha}=mg\sin{\alpha}.\]
Vydělíme rovnici výrazem \(\frac{mg}{\cos{\alpha}}\). Dostaneme:
\[f = \tan{\alpha}.\]
Po dosazení již snadno určíme hledaný úhel:
\[\alpha = \arctan {0{,}37} = 20{,}3^{\circ}.\]
Aby se bedna rozjela, musí chlapec zvednout desku o maličko více.
Nápověda g)
Připomeňte si, co platí pro velikosti součinitelů klidového a smykového tření. Jaká bude výslednice sil poté, co se bedna rozjede, a jakým pohybem bude sjíždět?
Řešení g)
Bedna sjíždí po nakloněné desce. Smyková třecí síla je menší než klidová třecí síla a výslednice sil působících na bednu je tedy nenulová. Označme tuto výslednici \(\vec{F_\mathrm{c}}\).
Do obrázku zakreslíme jen síly či jejich složky ve směru osy x, protože ty ovlivňují pohyb bedny. Jelikož tření, ke kterému dochází, je dynamické, označme třecí sílu \(\vec{F_\mathrm{dt}}\).
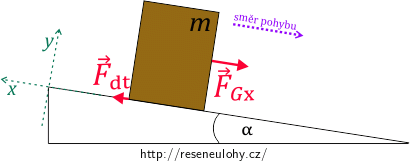
Sestavme pohybovou rovnici (pouze pro směr x):
\[\vec{F_\mathrm{dt}}+\vec{F_{\mathrm{G}_x}} = \vec {F_\mathrm{c}} = m\vec {a}.\]
Přepíšeme skalárně:
\[F_\mathrm{dt}-F_{\mathrm{G}_x} = -ma.\]
Velikost síly \(F_\mathrm{Gx}\) určíme podle vztahu (4). Velikost třecí síly \(F_\mathrm{dt}\) určíme obecně jako \(F_\mathrm{dt}=Nf_d\), kde \(f_\mathrm{d}\) je koeficient dynamického tření mezi bednou a deskou. Normálou, silou kolmou na podložku, je zde opět \(F_\mathrm{Gy}\). Podrobnou úvahu si můžete přečíst v řešení části úlohy f.
Dostaneme tedy:
\[mgf_\mathrm{d}\cos{\alpha}-mg\sin{\alpha}=-ma.\tag{6}\]
Nyní potřebujeme určit velikost zrychlení \(a\). Bedna urazí za čas \(t = 3\,\mathrm{s}\) dráhu \(s = 2\,\mathrm m\). Pohyb bedny je rovnoměrně zrychlený. Pro dráhu rovnoměrně zrychleného pohybu platí
\[s=\frac{1}{2}at^2.\]
Čas a dráhu známe, vyjádříme tedy zrychlení \(a\):
\[a = \frac{2s}{t^2},\]
\[a = \frac{2{\cdot} 2}{3^2}\,\mathrm{ms^{-2}}=0{,}44\,\mathrm{ms^{-2}}.\]
Dosazením do rovnice (6) za \(a\), získáme rovnici s jednou neznámou \(f_\mathrm{d}\), kterou vyjádříme:
\[f_\mathrm{d} = \frac{mg\sin{\alpha}−m\frac{2s}{t^2}}{mg\cos{\alpha}}.\]
Výraz upravíme a dosadíme číselně:
\[f_\mathrm{d} = \frac{g\sin{\alpha}−\frac{2s}{t^2}}{g\cos{\alpha}},\]
\[f_\mathrm{d} = \frac{10\cdot\sin{20{,}3^\circ}−\frac{2{\cdot} 2}{3^2}}{10\cdot\cos{20{,}3^\circ}},\]
\[f_\mathrm{d}=0{,}32.\]
Odpověď a)
Velikost maximální klidové třecí síly je \(111\,\mathrm N\).
Odpověď b)
Bedna se nepohne.
Odpověď c)
Podlaha na bednu působí třecí silou o velikosti \(90\,\mathrm N\).
Odpověď d)
Druhý chlapec musí na začátku zatáhnout o maličko větší silou než 57 N, aby se bedna rozjela.
Odpověď e)
Druhý chlapec musí na začátku zatáhnout ve vodorovném směru o maličko větší silou než 21 N, aby se bedna rozjela.
Odpověď f)
Chlapec musí desku zvednout o trochu větší úhel než \(\alpha = 20{,}3^{\circ}\).
Odpověď g)
Koeficient dynamického tření je \(f_\mathrm{d}=0{,}32\).