Pozor, padá tyč!
Úloha číslo: 526
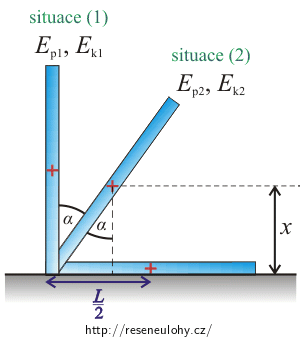
Homogenní tyč o hmotnosti M a délce L svisle postavená na vodorovné podložce volně padá z této polohy tak, že dolní konec po podložce neklouže. Dokažte, že pro úhlovou rychlost platí \(\omega^2=\frac{3g(1-\cos\alpha)}{L}\), kde α je úhel, který svírá tyč v daném okamžiku se svislou osou.
Moment setrvačnosti:
Tabulky udávají pro otáčení homogenní tyče délky L a hmotnosti M kolem jednoho z konců moment setrvačnosti
\[J=\frac{1}{3}ML^2\,.\](Odvození tohoto vztahu je uvedeno v úloze Moment setrvačnosti tyče.)
Nápověda
Úlohu lze snadno řešit s využitím zákona zachování mechanické energie. Vyberte dvě situace, ve kterých budete mechanickou energii srovnávat. Nezapomeňte zvolit hladinu nulové potenciální energie.
Podobná úloha
Vyřešeno? Vyzkoušejte si i podobnou úlohu Zavěšená tyč.