Auto, chodec, cyklista - grafy s, v
Úloha číslo: 226
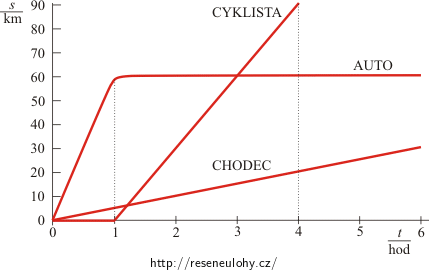
Auto, chodec a cyklista se pohybují po stejné silnici. Na obrázku je graf závislosti jejich drah na čase. Určete:
a) který z nich má během prvních tří hodin pohybu nejvyšší průměrnou rychlost,
b) po jaké době se potkal cyklista s autem,
c) nakreslete grafy závislosti velikostí jejich rychlostí na čase (pro přehlednost nejlépe každý graf do zvláštního obrázku).
Nápověda 1 – průměrná rychlost
Rozmyslete si, jak se počítá průměrná rychlost a kde se v grafu dají nalézt potřebné údaje.
Nápověda 2 – setkání auta s cyklistou
Jak lze z grafu závislosti dráhy na čase poznat, kdy se auto a cyklista potkali?
Rozmyslete si, co vyjadřují jednotlivé body v grafu závislosti dráhy na čase.
Nápověda 3 – graf závislosti v(t)
Uvědomte si, kde je v grafu závislosti dráhy na čase schovaná velikost rychlosti a zda se během pohybu jednotlivých objektů mění, či ne.
Rozmyslete si také, jak z grafu zjistíte konkrétní hodnotu rychlosti.
Celkové řešení
a) Průměrná rychlost
Průměrná rychlost se počítá jako podíl celkové dráhy, uražené za určitou dobu, a celé této doby.
K určení průměrné rychlosti auta, cyklisty a chodce tedy stačí zjistit z grafu jakou dráhu urazili za první tři hodiny. Auto a cyklista urazili 60 km a chodec urazil 15 km. Nyní průměrnou rychlost spočítáme tak, že tuto dráhu vydělíme třemi hodinami.
Průměrná rychlost auta:
\[v_{1} \,=\, \frac{60}{3}\,\mathrm{\frac{km}{h}}\,=\,20\,\mathrm{\frac{km}{h}}\,.\]Průměrná rychlost cyklisty:
\[v_{2} \,=\, \frac{60}{3}\,\mathrm{\frac{km}{h}}\,=\,20\,\mathrm{\frac{km}{h}}\,.\]Průměrná rychlost chodce:
\[v_{3} \,=\, \frac{15}{3}\,\mathrm{\frac{km}{h}}\,=\,5\,\mathrm{\frac{km}{h}}\,.\]b) Setkání auta a cyklisty
Každý bod grafu závislosti dráhy na čase určuje, jak daleko od počátku je těleso v daný okamžik.
Pokud se mají auto a cyklista potkat, musí se pohybovat po stejné trase a být ve stejný čas stejně daleko od počátku. To znamená, že se příslušné křivky musí protnout.
V našem případě se auto a cyklista potkají ve vzdálenosti 60 km od počátku, a to po třech hodinách od chvíle, kdy vyjelo auto, a dvou hodinách poté, co vyjel cyklista.
c) Závislost velikosti rychlosti na čase
Velikost rychlosti je schovaná ve sklonu křivky určující závislost dráhy na čase.
Přímka rovnoběžná s osou x znamená, že se těleso nepohybuje. Pokud se sklon křivky nemění, znamená to, že se nemění ani velikost rychlosti a jedná se o rovnoměrný pohyb.
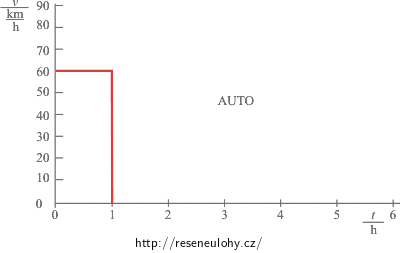
Auto
Během první hodiny má křivka stálý sklon, velikost rychlosti se tedy neměnila. Auto ujelo za tuto hodinu 60 km, a jelo proto rychlostí 60 km za hodinu. Během dalších dvou hodin se jeho vzdálenost od počátku nezvětšovala, přímka je rovnoběžná s osou x, rychlost auta byla tedy nulová.
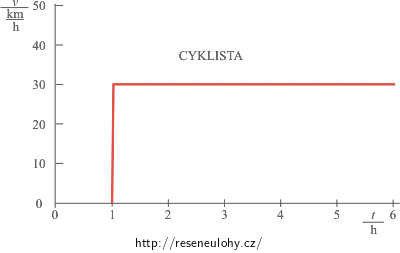
Cyklista
Cyklista první hodinu stál na místě, jeho rychlost byla nulová (křivka splývá s osou x). Dále je grafem závislosti dráhy na čase přímka (ta má stálý sklon) a velikost rychlosti cyklisty se tedy neměnila. Z grafu můžeme odečíst, že za dvě hodiny ujel cyklista 60 km. Jeho rychlost byla tedy 30 km za hodinu.
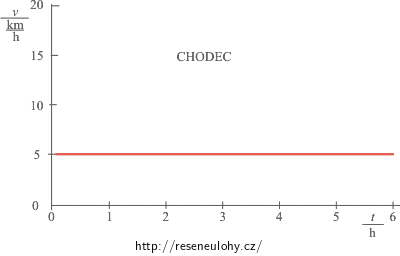
Chodec
Grafem závislosti dráhy na čase pro chodce je přímka. Chodec šel po celé tři hodiny rovnoměrně, stálou rychlostí, a urazil 15 km. Jeho rychlost byla po celou dobu 5 km za hodinu.
Odpověď
a) Největší průměrnou rychlost mělo auto a cyklista, a to shodně 20 km/h.
b) Auto a cyklista se potkají ve vzdálenosti 60 km od počátku, a to po třech hodinách od chvíle, kdy vyjelo auto, a dvou hodinách poté, co vyjel cyklista.
c) Grafy závislostí velikosti rychlosti na čase: