Napětí na průřezu nosníku
Úloha číslo: 2159
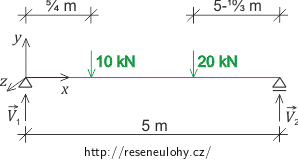
Na obrázku je ocelový nosník délky 5 m. Nosník je v první čtvrtině své délky zatížen svisle dolů silou 10 kN a ve dvou třetinách své délky je zatížen svisle dolů silou 20 kN. Všechna zatížení míří k těžišti průřezu. Na oba jeho konce působí vazbové síly, při nichž je nosník v rovnováze. Určete, zda dojde k většímu ohybu nosníku, to znamená k větší deformaci, pro obdélníkový průřez, kde vodorovný rozměr je 0,1 m a svislý 0,2 m, nebo pro obdélníkový průřez, kde vodorovný rozměr je 0,2 m a svislý 0,1 m. Dále pro průřez s větším ohybem stanovte průběh napětí na kolmém průřezu v první třetině délky nosníku. Vlastní tíhu nosníku zanedbejte.
Zápis
l = 5 m délka nosníku F1 = 10 kN zatížení v první čtvrtině nosníku F2 = 20 kN zatížení v druhé třetině nosníku x1 = 5/4 m vzdálenost působiště první síly od počátku x2 = 10/3 m vzdálenost působiště druhé síly od počátku a1 = 0,1 m vodorovný rozměr průřezu pro první situaci b1 = 0,2 m svislý rozměr průřezu pro první situaci a2 = 0,2 m vodorovný rozměr průřezu pro druhou situaci b2 = 0,1 m svislý rozměr průřezu pro druhou situaci σ(y) = ? průběh napětí na kolmém průřezu Rozbor
Nejprve je třeba určit vazbové síly tak, aby nosník byl v rovnováze. Dále bude potřeba určit průběh momentů sil podél nosníku. Velikost deformace, tedy ohyb, závisí na velikosti kvadratického momentu průřezu. Kdybychom měli rovnici pro ohyb, bylo by zřejmé, že čím větší kvadratický moment je, tím menší je deformace. Vzhledem k podmínkám ze zadání pro průběh napětí použijeme vzorec, který uvažuje neutrální osu, tedy místo s nulovým napětím, procházející těžištěm průřezu. Podmínkou ze zadání je myšleno to, že moment sil vzniká kolem jediné osy.
Nápověda
Nejprve určete vazbové síly pro podmínku rovnováhy. Dále bude potřeba určit průběh momentů sil podél nosníku. V momentovém průběhu uvažujte celkový moment od sil vždy před proměnnou. Dále vypočítejte kvadratické momenty zadaných průřezů. Z toho již stanovte, pro který bude příslušná deformace, tedy ohyb, větší. Zatížení prochází těžištěm, silový moment vznikne pouze kolem jediné osy. Ve vhodném vzorci pro průběh napětí na průřezu uvažujte nulové napětí v místě těžiště.
Řešení
Na obrázku jsou vyznačeny síly působící na nosník.

Pro rovnováhu musí být splněno:
\[V_1+V_2\,=\,F_1+F_2,\tag{1}\]kde V1 je vazbová síla na levém konci nosníku, V2 je vazbová síla na pravém konci nosníku, F1 je síla působící ve čtvrtině nosníku a F2 je síla působící ve dvou třetinách nosníku. V rovnici (1) není zahrnuta vlastní tíha nosníku, kterou budeme uvažovat za zanedbatelnou. Protože máme dvě neznámé, můžeme ještě přidat podmínku pro rovnováhu momentů sil vzhledem k počátku, tedy:
\[lV_2\,=\,x_1F_1+x_2F_2.\tag{2}\]Pak tedy:
\[V_2\,=\,\frac{x_1F_1+x_2F_2}{l}.\tag{3}\]Dosazením (3) do (1) nám vyjde:
\[V_1\,=\,\frac{\left(l-x_1\right)F_1+\left(l-x_2\right)F_2}{l}.\tag{4}\]Dále budeme určovat průběh momentů, který bude funkcí vzdálenosti x. Tento průběh uvažuje pouze momenty sil před tím bodem nosníku, ve kterém moment počítáme. Kdybychom uvažovali momenty sil i za tímto bodem, pak by celkový moment byl samozřejmě nulový, protože nosník máme v rovnováze. K porozumění může posloužit obrázek.
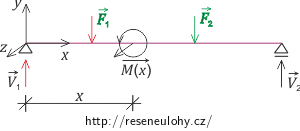
Ovšem zde zatížení není spojité, proto bude potřeba průběh momentu zapsat jen pro takový interval, kde nás napětí podle zadání zajímá. Momentový průběh dle obrázku, kde nás zajímají červěně vyznačené síly, zapíšeme na otevřeném intervalu od x1 do x2 ve tvaru:
\[M(x)\,=\,-V_{1}x+F_{1}\left(x-x_1\right).\tag{5}\]Ještě můžeme dosadit ze (4) do (5), takže:
\[M(x)\,=\,-\frac{\left(l-x_1\right)F_1+\left(l-x_2\right)F_2}{l}x+F_{1}\left(x-x_1\right).\tag{6}\]Abychom viděli, jak závisí deformace původně rovného nosníku na průřezu, podíváme se na ohybovou rovnici popisující tvar nosníku po deformaci:
\[\frac{\mathrm{d}^2y'(x')}{\mathrm{d}x'^2}\,=\,-\frac{M(x)}{EI}.\tag{7}\]Rovnici (7) najdete v běžně dostupné literatuře týkající se dané oblasti, ovšem je třeba dávat pozor na znaménko. To závisí nejen na orientaci os, ale i na tom, zda momentový průběh uvažujeme zleva doprava, či obráceně. Na levé straně jsou x a y s čárkou, protože je třeba proměnné od sebe rozlišovat. Z (7) vidíme, že zakřivení nosníku klesá s rostoucím kvadratickým momentem průřezu I. Kvadratický moment nám udává závislost ohybu na průřezu nosníku a čím menší I je, tím se nosník více deformuje. Jestliže je průřez obdélníkový, pak platí vztah:
\[I\,=\,\int_{-\frac{a}{2}}^{\frac{a}{2}}\int_{-\frac{b}{2}}^{\frac{b}{2}}y^2\mathrm{d}y\mathrm{d}z\,=\,\frac{ab^3}{12}.\tag{8}\]Pak dle (8) máme pro první průřez:
\[I_{1}\,=\,\frac{0{,}1{\cdot}0{,}2^3}{12}\mathrm{m^4}\,=\,\frac{2}{3}\cdot10^{-4}\mathrm{m^4}\]a pro druhý máme:
\[I_{2}\,=\,\frac{0{,}2{\cdot}0{,}1^3}{12}\mathrm{m^4}\,=\,\frac{1}{6}\cdot10^{-4}\mathrm{m^4}.\]Z předchozího vidíme, že pro druhý průřez dojde ke čtyřikrát větší deformaci.
Dále už pro výpočet průběhu napětí na kolmém průřezu v jedné třetině délky nosníku budeme uvažovat pouze druhý průřez. Budeme k tomu pro náš případ, kdy silový moment vzniká kolem jediné osy, potřebovat vzorec:
\[\sigma (y)\,=\,\frac{M(x)}{I}y.\tag{9}\]I v rovnici (9), podobně jako v (7), je třeba dávat pozor na znaménko. Nyní dosadíme z (6) a (8) do (9), takže:
\[\sigma (y)\,=\,-\frac{12}{ab^3}y\left[\frac{\left(l-x_1\right)F_1+\left(l-x_2\right)F_2}{l}x+F_{1}\left(x-x_1\right)\right].\tag{10}\]Silový moment vzniká pouze kolem osy z, protože zatížení míří k těžišti, takže v našem případě můžeme neutrální osu, tj. místo s nulovým napětím, uvažovat v těžišti průřezu. Těžiště homogenního obdélníku se nachází v polovině jeho šířky a a v polovině jeho výšky b. Zde tedy budeme uvažovat y na uzavřeném intervalu -b/2 až b/2, jestliže bereme počátek v těžišti. Nyní už jenom číselně dosadíme do (10), potom vyjde:
\[\sigma (y)\,=\,-\frac{12}{0{,}2{\cdot}0{,}1^3}\cdot{y}\cdot\left[\frac{\left(5-\frac{5}{4}\right)\cdot10{\cdot}10^3+\left(5-\frac{10}{3}\right)\cdot20{\cdot}10^3}{5}\frac{5}{3}+10{\cdot}10^3\cdot\left(\frac{5}{3}-\frac{5}{4}\right)\right] \mathrm{Pa},\]tedy:
\[\sigma (y)\,=\,-\frac{5}{3}\cdot{y} \mathrm{GPa},\]kde:
\[y\in\left[-\frac{1}{20} \mathrm{m};\frac{1}{20} \mathrm{m}\right].\]Ještě si všimněme, že podle znaménka pro horní polovinu průřezu dochází k tlaku a pro dolní k tahu. To je zřejmé už podle způsobu zatížení, a ukazuje to i fyzikální důvod, proč si v (9) uhlídat správné znaménko.
Odpověď
K většímu ohybu dojde pro druhý obdélníkový průřez, ohyb bude čtyřikrát větší.
Průběh napětí na kolmém průřezu v první třetině nosníku je:
\[\sigma (y)\,=\,-\frac{5}{3}\cdot{y} \mathrm{GPa},\]kde:
\[y\in\left[-\frac{1}{20} \mathrm{m};\frac{1}{20} \mathrm{m}\right].\]

